문제 내용
Stones가 쌓여있는 길이 Arrays가 주어졌을 때 Stones 사이에 얼마나 많은 물이 쌓일 수 있는가?
풀이 방법
풀이 방법은 여러가지가 있을 수 있는데 가장 쉬운 방법은
왼쪽에서 부터 포지션을 하나씩 늘려가면서, 현재 포지션의 왼쪽과 오른쪽을 Full Search한 후 왼쪽과 오른쪽의 가장 높은 높이를 찾고 그중 낮은 값을 답으로 하면된다.
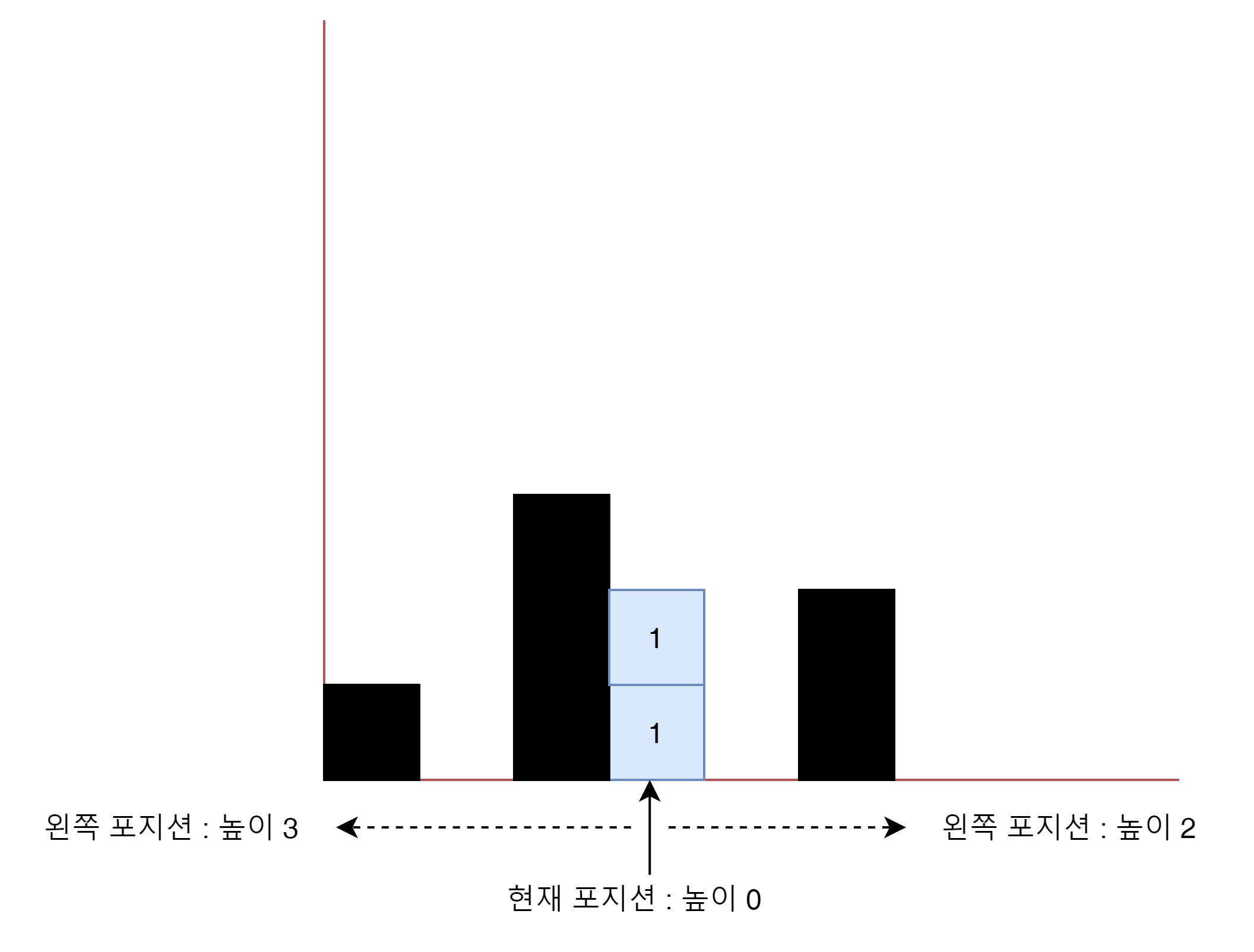
상기 그림을 보면 왼쪽 포지션과 오른쪽 포지션을 보고 가장 낮은 포지션의 값인 2을 현재 포지션의 물 높이로 선택 하면 된다.
그런데 이렇게 full search 하게 되면
Height의 Size N 만큼 왼쪽으로 움직일 때마다 (N-1) 만큼의 Search가 매번 필요하다.
수식으로 하면 O(N*(N-1))이 됨으로 O(N^2)이 되게 된다.
이를 최적화 하기 위해서 다음과 같이 2 Points를 사용하면 쉽다.

왼쪽과 오른쪽 양쪽 끝의 Points를 유지 하면서 양쪽의 Max 높이를 유지 하는 방식이다.
기본적으로 왼쪽의 높이가 오른쪽의 높이보다 작다면 우측으로 현재 포지션을 움직이면 된다.
반대인 경우는

오른쪽의 포지션을 왼쪽으로 움직이면서 현재 포지션을 변경해 준다.
잡힌 물의 높이는

왼쪽의 높이와 오른쪽의 높히 중에 낮은 값을 선택하고 현재 위치의 돌의 높이를 빼주면 된다.
이를 Sample 문제에 대입하자면 다음과 같다

현재의 포지션을 한번씩만 움직임으로 O(N)으로 충분하다.
주의 해야할 Edge 포인트는 Height의 길이가 3이상이어야 한다는 것이다.
물을 가두기 위해서는 무조건 길이 3이상이 필요하다는 것이다.
코드는 아래와 같다.
public class TrappingWater {
public int trap(int[] height) {
if (height.length < 3) {
return 0;
}
int leftIdx = 0;
int rightIdx = height.length - 1;
int leftMaxHeight = height[0];
int rightMaxHeight = height[rightIdx];
int traps = 0;
while (leftIdx < rightIdx) {
int curPosition = -1;
if (height[leftIdx] <= height[rightIdx]) {
leftIdx++;
curPosition = leftIdx;
leftMaxHeight = Math.max(leftMaxHeight, height[curPosition]);
} else {
rightIdx--;
curPosition = rightIdx;
rightMaxHeight = Math.max(rightMaxHeight, height[curPosition]);
}
int temp = Math.min(leftMaxHeight, rightMaxHeight) - height[curPosition];
if (0 < temp) {
traps += temp;
}
}
return traps;
}
public static void main(String[] args) {
TrappingWater trappingWater = new TrappingWater();
int[] inputs = {1,0,2};
System.out.println(trappingWater.trap(inputs));
}
}
'Problem Solving' 카테고리의 다른 글
| Consecutive Numbers Sum (0) | 2021.04.28 |
|---|---|
| Basic Calculator (0) | 2021.04.27 |
| Buddy Strings (0) | 2020.10.12 |
| Count Subtrees With Max Distance Between Cities (0) | 2020.10.12 |
| Two Sum III - Data structure design (0) | 2020.10.10 |
