Longest Repeating Character Replacement
문제 내용
주어진 문자열에서 k만큼의 문자를 다른 문자로 교체가 가능하다고 했을 때, 동일한 문자로 가장 길게 만들 수 있는 문자의 길이는 얼마인가?
접근 방법
Brute Force
가장 쉬운 방법은 모든 point에서 loop를 도는 것이다.
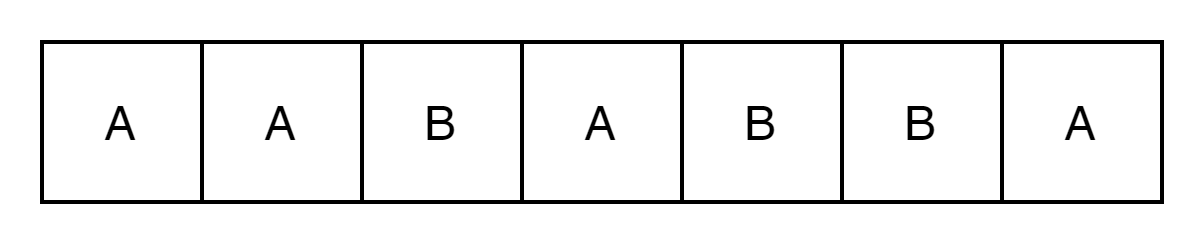
위와 같은 문자열이 있을 때, k 즉 교체 가능한 문자열의 횟수는 1회라고 생각해 보자.
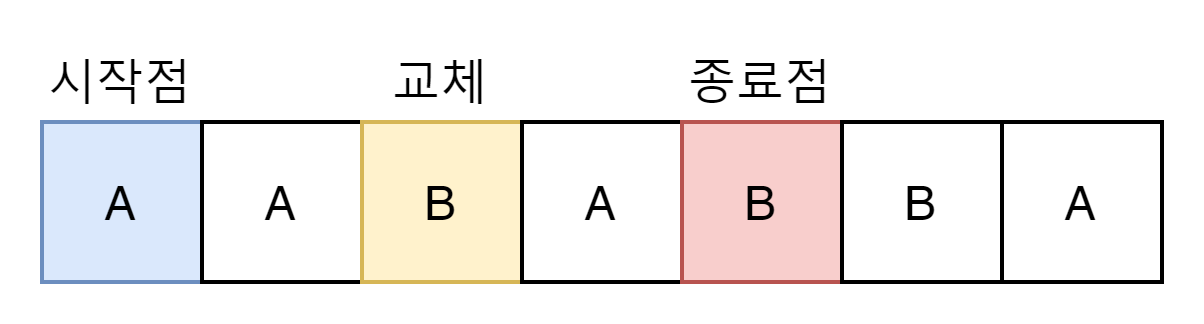
이렇게해서 4라는 길이가 나올 수 있다.
그럼 다시 그다음 A에서 실행해 보자.

앞서와 동일한 종료점을 갖는다.
다음은 B이다
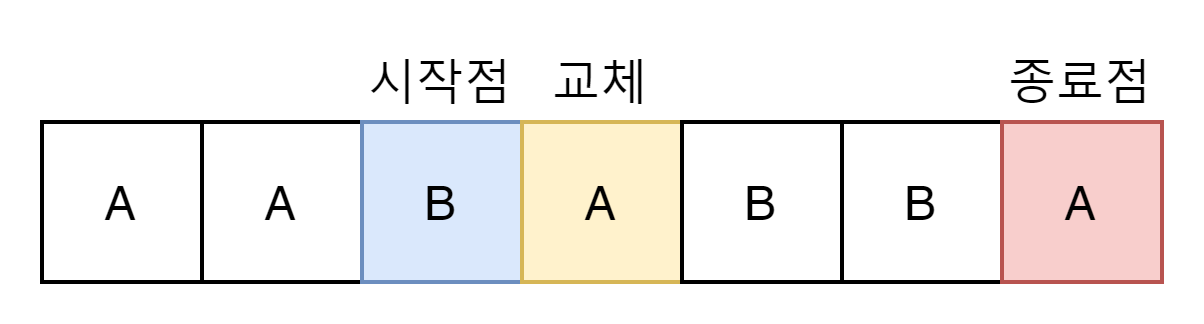
B도 4라는 길이가 나올 수 있다. 정답은 4가 되게 된다.
이 방식은 O(N^2) 이 된다. 이것을 최적화가 필요하다.
Memorization
Brute Force의 내용을 보면 모든 포인트를 looping 할 필요 없이 교체점이 되는 부분만 계산을 해서 처리 하면 된다는 것을 알 수 있다. 예를 들자면


위의 2경우는 동일하다. 즉 다음 시작 점은 교체점인 B에서만 한번더 looping을 돌면 된다.
이렇게 꼭 필요한 곳만 진입을 해서 그 max 값을 알면 되는데, 이때 visited를 이용해서 앞서 visited가 이미 된 point는 계산을 하지 않도록 만들어 준다.

이 방식을 사용하면 모든 Point에 대한 Max 값을 찾지 않아도 되니 속도에 개선은 이루어 질 수 있다.
단지, 'ABCDEFGH' 이런식으로 모든 값이 다를 경우 $ O(N^2) $ 인것은 변함이 없게 된다.
var characterReplacement = function(s, k) {
const stack = new Array();
const visited = new Array(s.length).fill(false);
let max = 0;
stack.push(0);
while(0 < stack.length){
let point = stack.shift();
let hold = s.charAt(point);
let ticket = k;
let count = 1;
for(let i = point + 1; i < s.length && max <= s.length - point && 0 <= ticket; i++){
if(s.charAt(i) !== hold) {
ticket--;
if(!visited[i]){
stack.push(i);
visited[i] = true;
}
}
if(0 <= ticket){
count++;
}
}
max = Math.max(max, count + (0 < ticket? ticket : 0));
}
return Math.min(max, s.length);
};
Sliding windows
two points를 이용해서 최대 길이를 유지 하는 방식이다.
우선 다음의 경우를 생각해 보자.
임의의 범위에서 최대 길이는 무었을 기준으로 할까?

위와 같이 ABCB라고 하는 부분 집합을 보자. 무슨 값을 기준으로 최대 길이를 구할 수 있을까?
말할 필요 없이 B가 될 것이다. B는 2개의 count가 있고 k가 1이상이기만 하면
- B count 갯수 + k
가 답이 된다.
그런데 만약에 k가 0이면 'B count 갯수 + k'라는 공식은 의미가 없게 된다.
여기서 중요한것은 k가 유지되는 범위내에서 sub sequence를 잡아야 한다는 것이다.
예를 들어보자
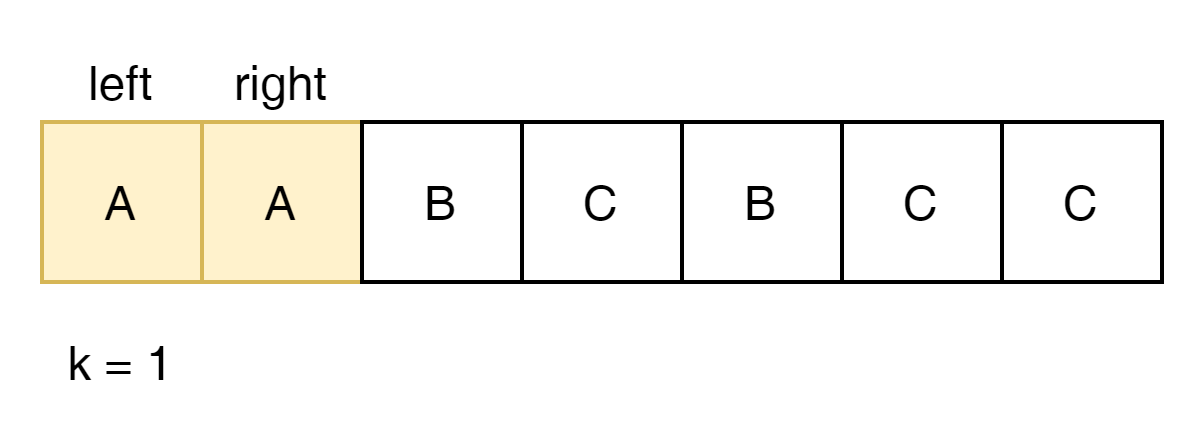
left가 0이고 end가 1이면 A가 가장 많이 출현하였음으로 2 + 1(k) 이 현재까지 Max가 된다.

k가 있기 때문에 우측으로 한칸 더 가볼 수 있다. 그리고 여전히 A가 가장 많이 출현 하였음으로 2 + 1이 max가 된다.
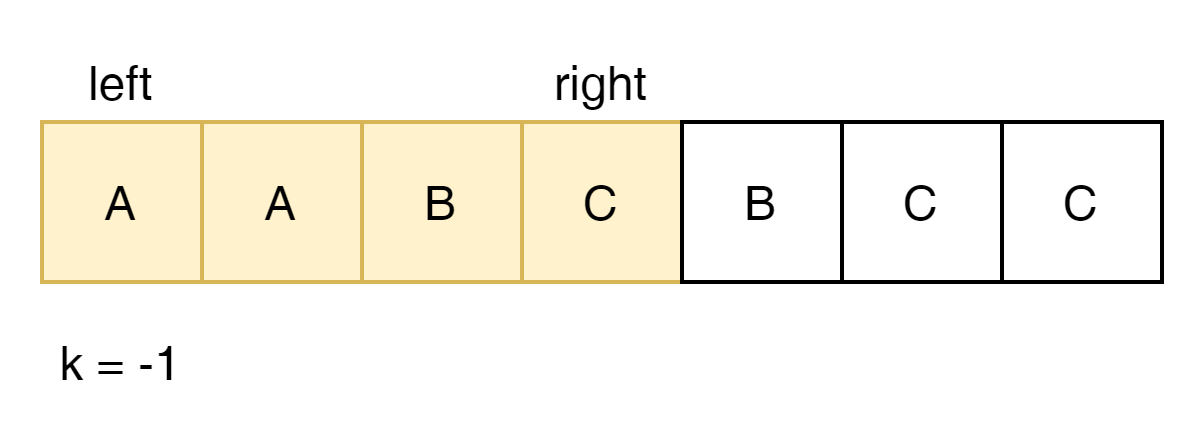
우측으로 한칸더 가는 것은 불가능하다. k가 음수가 되었다. left를 욺직여야 할 때이다.

위 그림을 보자면 문제가 발생한다. A가 더이상 가장 많이 출현하지 않는다는 것이다. 그리고 k를 더한다고 해도 2 즉 위의 sub sequence 3을 만족시킬 수 없다.
이 문제를 해결하기 위해서 이제부터 max의 대상은 right가 진입한 char의 출현횟수 또는 그 이전까지 출현한 max의 값을 기준으로하자.
right가 진입한 char의 출현횟수가 더 많으면 해당 sub sequence는 그 출현횟수가 major가 되게 된다.
위는 여전히 max는 2가 유지된다. C가 1회 출현했기 때문이다. 그런데 이런 의문이 들수 있다. MAX즉 A의 count는 괜찮은건가?
아니다 안괜찮다. 그래서 A의 count 횟수는 1 줄여줘야 한다.

그럼 max도 1로 줄이는게 맞지 않을까? 맞긴 하다. A가 가장 많이 출현했다는 것을 기록한다면 말이다.
하지만 그 부분은 일단 무시하고 진행해 보자.

이제 최대 출현수는 B의 2가 되고 max도 2가 되었다. left와 right의 길이는 4가 되었고 max에 k값 1을 더해도 4에 도달 할수 없다는 것을 알게 되었다.
left를 줄여줘야 한다.
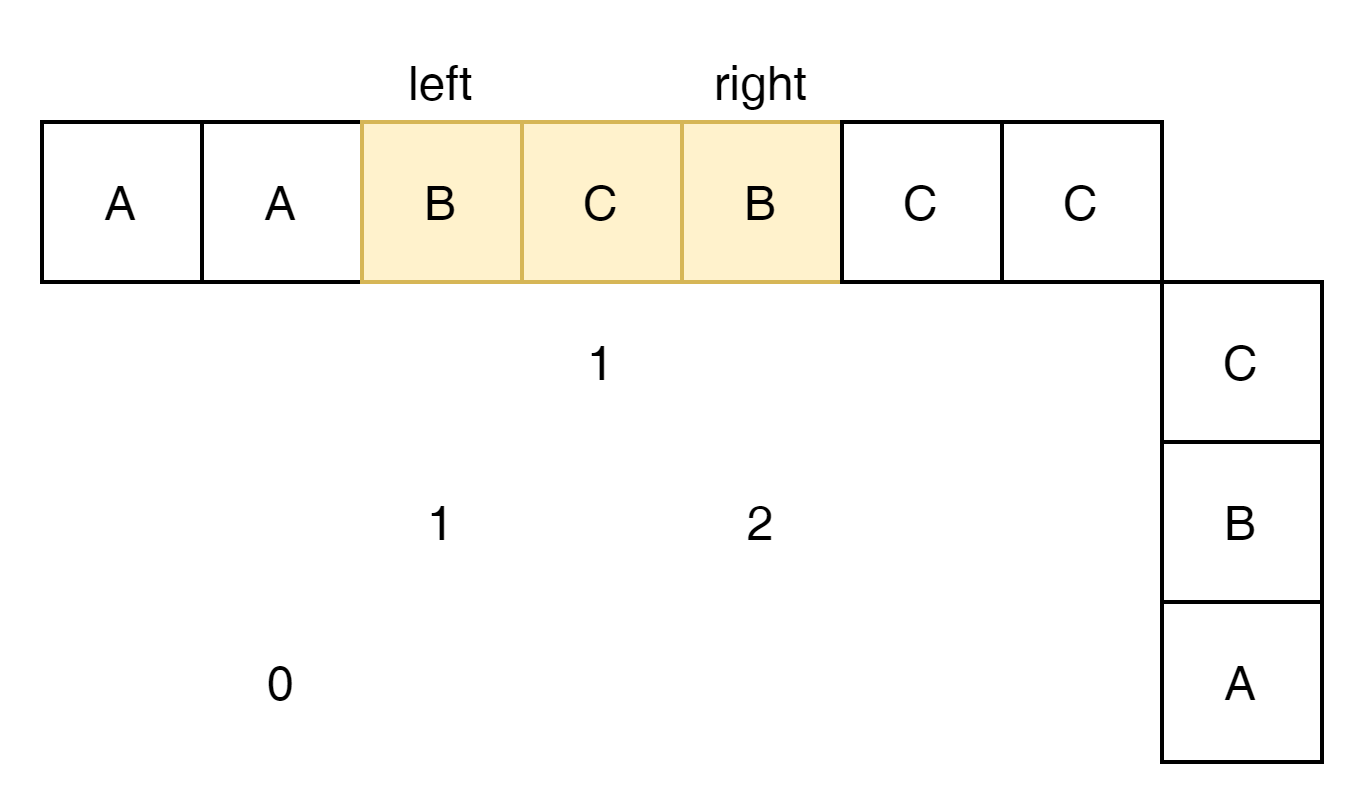
A의 count는 이제 더이상 불필요 하다. B 2개와 k1개로 3이 가능하다.
우측으로 더 가자.
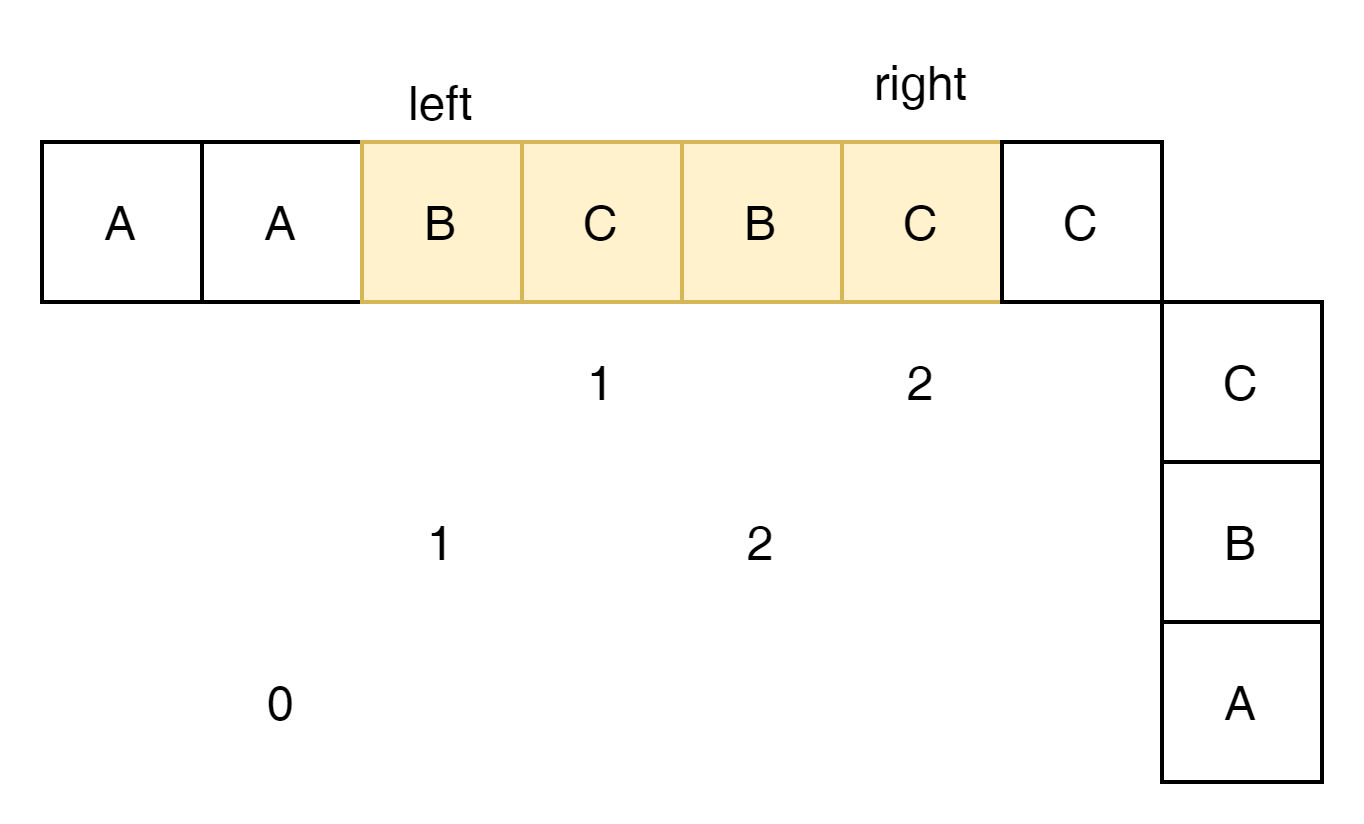
max 2에 1을 더한다고 해도 길이 4를 감당할 수는 없다.
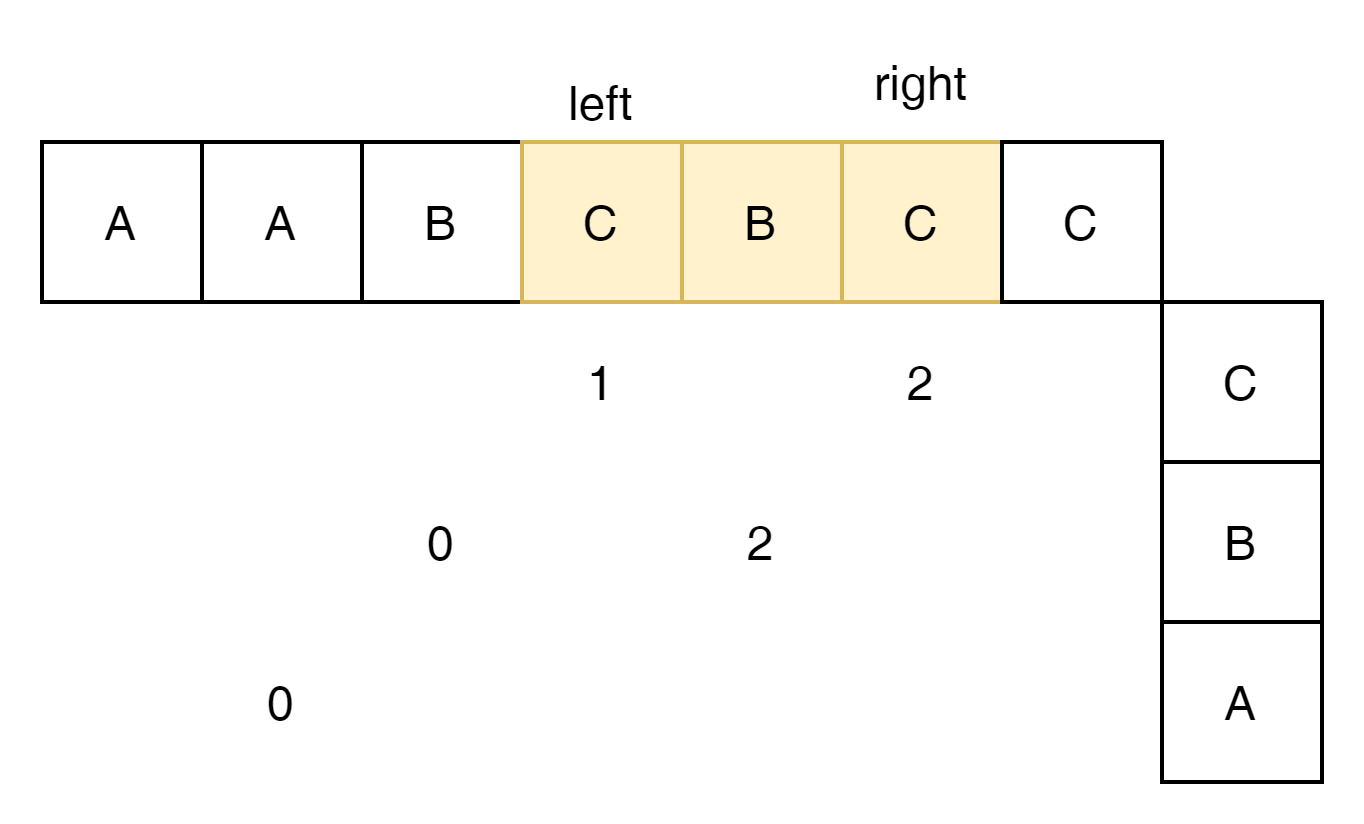
left를 옮기고 right를 더하자.
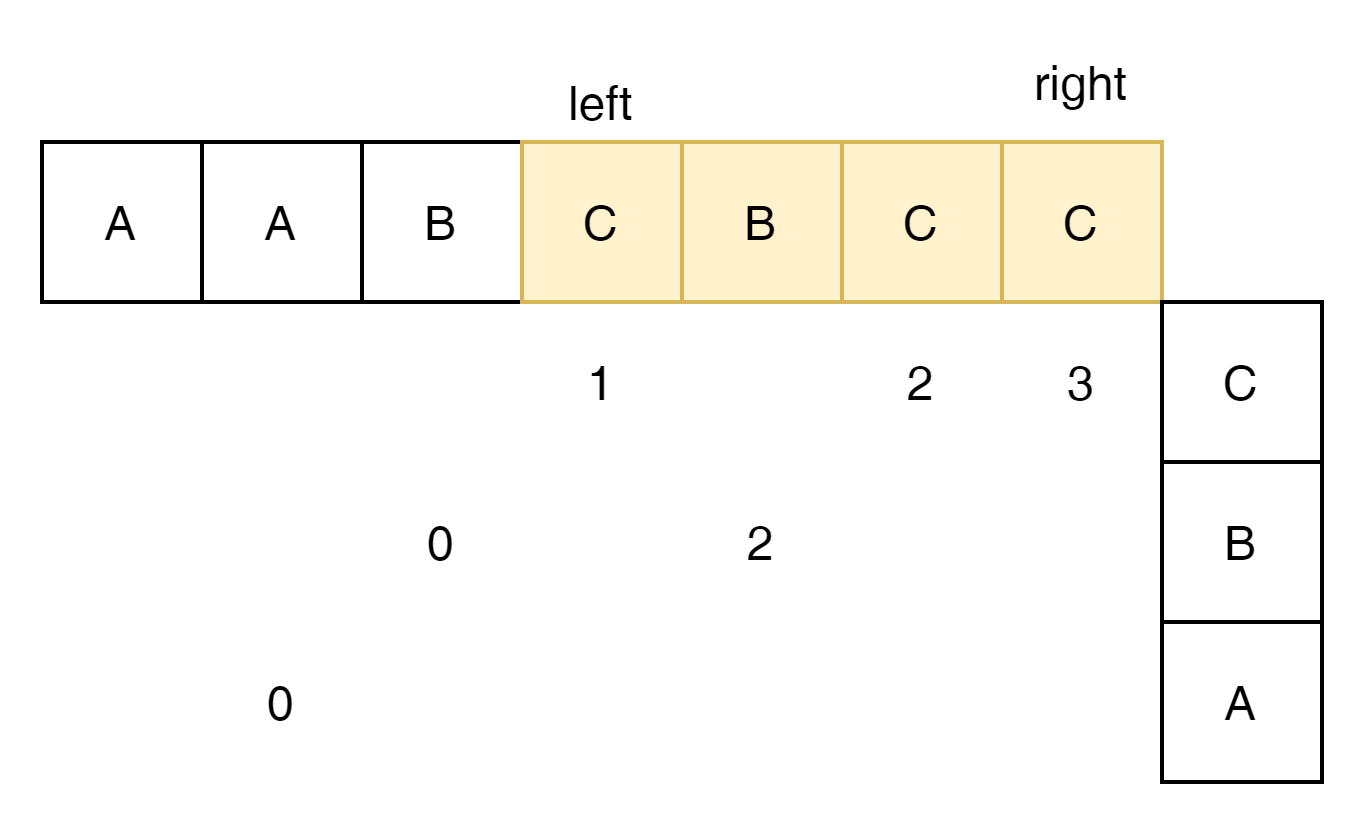
C가 3개이고 k가 1임으로 max 4가 답이 된다.
이 문제의 답은 subsequence 내의 가장 많이 발생하는 "문자의 횟수 + k" 가 답이 된다.
var characterReplacement = function(s, k) {
const arr = new Array(26).fill(0);
let left = 0;
let max = 0;
let result = 0;
for(let right = 0; right < s.length; right++){
max = Math.max(max,++arr[s.charCodeAt(right) - 'A'.charCodeAt(0)]);
result = Math.max(result, max + k);
if(max + k < right - left + 1){
arr[s.charCodeAt(left) - 'A'.charCodeAt(0)]--;
left++;
}
}
return Math.min(result,s.length);
};그런데 재미있게도
s.length - left를 해도 동일한 답이 된다.
var characterReplacement = function(s, k) {
const arr = new Array(26).fill(0);
let left = 0;
let max = 0;
for(let right = 0; right < s.length; right++){
max = Math.max(max,++arr[s.charCodeAt(right) - 'A'.charCodeAt(0)]);
if(max + k < right - left + 1){
arr[s.charCodeAt(left) - 'A'.charCodeAt(0)]--;
left++;
}
}
return s.length - left;
};시간복잡도는 $$ O(N) $$ 이다
Maximize the Confusion of an Exam
위와 동일한 방식의 문제가 출제 되었다.
참고하자.
'Problem Solving' 카테고리의 다른 글
| Sparse Matrix Multiplication (0) | 2021.08.17 |
|---|---|
| Javascript 32bit 이상 Number&Integer 계산하기 (BigInt) (1) | 2021.08.14 |
| Power of Four (0) | 2021.08.13 |
| Data Stream as Disjoint Intervals (0) | 2021.08.10 |
| Hamming Distance (0) | 2021.08.09 |
