Remove Max Number of Edges to Keep Graph Fully Traversable
Remove Max Number of Edges to Keep Graph Fully Traversable - LeetCode
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com

- 문제 내용 : 3개의 타입이 주어지는 그래프이다.
- 1번 타입 : Alice 혼자 접근 가능한 Edges 그룹
- 2번 타입 : Bob 혼자 접근 가능한 Edges 그룹
- 3번 타입 : Alice와 Bob 양쪽다 접근 가능한 Edges 그룹
해당 그래프를 그리는 Edges 그룹을 Array로 제공한다.
해당 그룹에서 Alice와 Bob이 전체 Node를 Travel할 수 있는 최소한의 Edges만 남기고, 몇개의 Edges를 삭제 해도 되는지 결과를 내놓으면 된다.
- 접근
3번 타입으로 할 수 있는 최소 Node graph를 그리고, 1번 2번을 각각 자신의 Edges를 추가해서 모든 노드를 Travel 할 수있도록 한다.
나의 첫번째 접근 : Dijkstra Algorithm
- 3번 타입으로 Shortest Path 노드를 그리고 해당 Node에 포함 되지 않는 Edges를 삭제 한다.
- 삭제된 3번 타입 Shortest Path에 1번과 2번 Edges를 넣어서 Nodes에 포함 되지 않는 Edges를 삭제 한다.
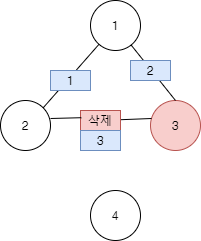
상기 이미지를 보면 [[1,2],[1,3],[2,3]] 이라고 했을 때, 3번 노드의 Edge Cost 최저가 1 -> 3 으로 1이다. 그런데 2 -> 3접근을 할때 3의 cost는 2가 된다. 당연히 Shortest이기 때문에 2는 무시 된다. 이렇게 무시 되는 시점에 Result Count 를 1더하는 방식이다.
이 방식을 3번 타입 -> (1번 타입, 2번타입)을 처리 하면 된다.
Dijkstra Algorithm을 통해서 해당 행위를 하려고 했으나, 코드량이 많아 지면서 error를 많이 만들어 내서 포기 했다.
지금도 가능할 것이라 생각하는데... 쉽지 않았다.
Cost에 대한 대응 보다는 Travel 가능한 Point가 가능한지를 파악하는 Union Find로의 접근이 확실히 효과적이라고 생각한다.
두번째 접근 : Union Find
언제쯤 시간안에 Contest를 다 풀수 있을 지 모르겠다. 언젠가 그런날이 오면 기분 좋을 거 같다.
다른 사람 풀이를 보고 본 문제를 풀었다.
[Python] Union Find - LeetCode Discuss
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
상기 풀이가 오리지널 이다.
Union Find는 아래와 같은 프로세스를 따른다.
- 각 Node의 Parent를 찾는다.
- 각 Parent 중 x 또는 y쪽으로 Parent를 정한다
아래의 경우 오른쪽 Node Point를 중심으로 Parent를 정한 것이다. - Node의 Parent를 찾을때는 find를 사용한다
- find를 찾을 때 반듯이 Parent를 정렬해 준다.
아래 그림에서 보자면 1의 Parent를 찾기 위해 2,3을 지나서 Parent 4를 찾게 되는데, 최종적으로 1,2,3은 4를 Parent로 대응 하게 한다. 이러한 행위는 find를 하면서 한번에 처리 해줘야 한다.
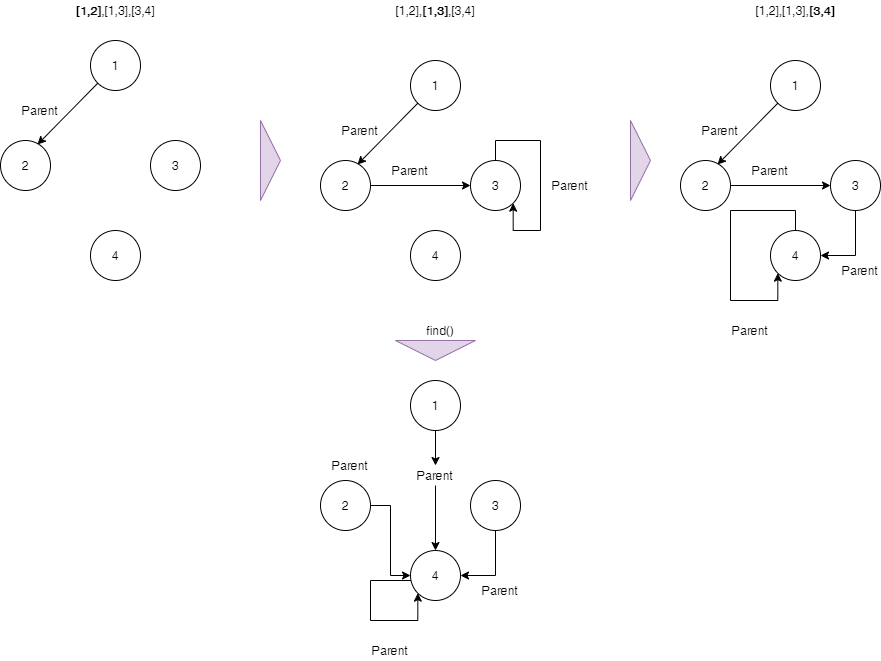
상기 프로세르를 완성 한후 이미 지정된 포인트에 대한 Edge가 다시 들어오게 된다면 그때부터 Ignore 하면된다.
가령 [2,3]이 들어온다면 2의 Parent는 4이고 3의 Parent도 이미 4이다. 두 포인트는 이미 Union이 된 상태임으로 [2,3] Edge는 불필요 하다.
var maxNumEdgesToRemove = function(n, edges) {
let root = new Array(n + 1);
let alice = 0;
let bob = 0;
let result = 0;
for (let i = 0; i < n + 1; i++) {
root[i] = i;
}
for (let i = 0; i < edges.length; i++) {
let [idx, x, y] = edges[i];
if (idx == 3) {
if (union(x, y)) {
alice++;
bob++;
} else {
result++;
}
}
}
let copy = JSON.stringify(root);
root = JSON.parse(copy);
for (let i = 0; i < edges.length; i++) {
let [idx, x, y] = edges[i];
if (idx == 1) {
if (union(x, y)) {
alice++;
} else {
result++;
}
}
}
root = JSON.parse(copy);
for (let i = 0; i < edges.length; i++) {
let [idx, x, y] = edges[i];
if (idx == 2) {
if (union(x, y)) {
bob++;
} else {
result++;
}
}
}
return alice == n-1 && bob == n-1 ? result : -1;
function find(i) {
if(root[i] != i){
root[i] = find(root[i]);
}
return root[i];
}
function union(x, y) {
x = find(x);
y = find(y);
if (x == y) {
return false;
} else {
root[x] = y;
return true;
}
}
}'Problem Solving' 카테고리의 다른 글
| Word Pattern (0) | 2020.09.07 |
|---|---|
| 835. Image Overlap (0) | 2020.09.07 |
| 5509. Minimum Deletion Cost to Avoid Repeating Letters (0) | 2020.09.06 |
| 5508. Number of Ways Where Square of Number Is Equal to Product of Two Numbers (0) | 2020.09.06 |
| 5507. Replace All ?'s to Avoid Consecutive Repeating Characters (0) | 2020.09.06 |
