Minimum Cost to Connect Two Groups of Points
Minimum Cost to Connect Two Groups of Points - LeetCode
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
- 문제 내용 : A Group Points와 B Group Points 간의 연결시 Cost가 Array로 주어졌을 때 양쪽의 모든 Point가 서로 모두 연결 되었을 때의 최소값을 찾아라
- 접근 방법 : 전 탐색
늘 다른 사람 답을 보고 문제를 풀었지만, 이번 문제는 답을 보고도 몇시간을 헤매다가 답을 이해했다.
기본적인 문제 해결 방법은 문제 초기 생각 했었지만, 이를 코드로 옮긴다는게 굉장히 힘들었다.
- 초기 접근 방법 : A group에 있는 포인트들의 최소값으로 B Point를 찾고 B Point 중 연결되어있지 않은 포인트 대상으로 최소값 연결을 찾아 A를 연결한다.
그런데 상기 접근이 불가 했던게, 다중 포인트 연결의 경우 최소값을 찾을 수가 없었다.
다른 사람의 접근 방법을 보니 모두 전 탐색을 처리 하고 있었다.
전탐색 문제가 나오게 되면 이게 최적화 과정이 가능한지 여부를 알수가 없어서 어려움이 많다.
상기 링크에 있는 코드를 바탕으로 코드를 설명 하고자 한다.
- A Group의 첫번째 포인트 부터 마지막 포인트까지 Permutation 처리 하면서 전탐색을 처리 한다.
- A Group 전 탐색 처리가 완료 되면 B Group에 연결되지 못한 포인트를 찾아 최소값을 더해준다.
상기 1번과 2번을 그림으로 보면 다음과 같다.
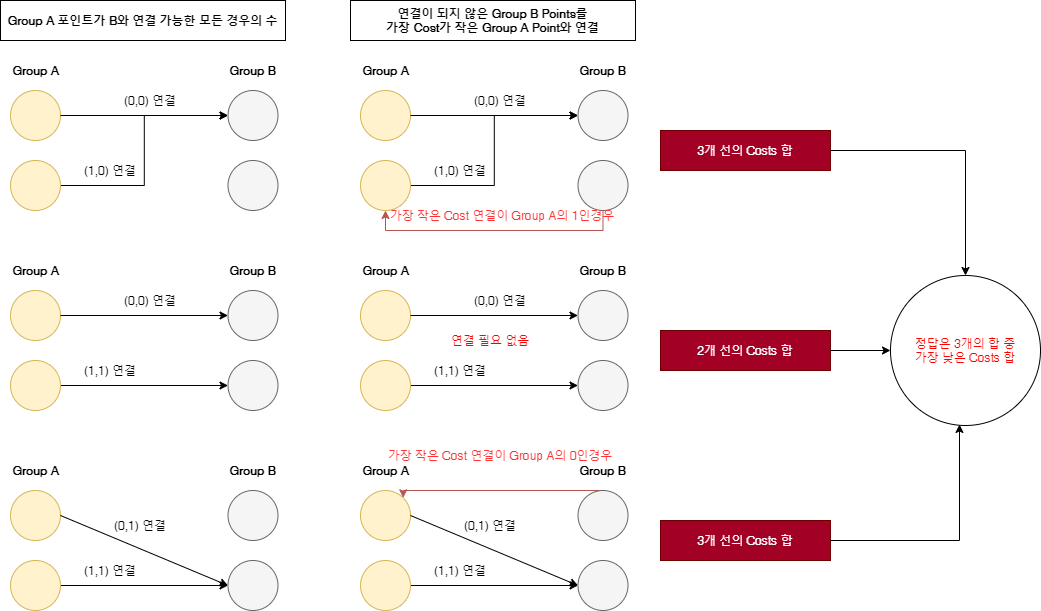
상기 그림을 예로 보자면 다음과 같다.
문제 [[1,2][3,4]]가 주어진다면
Group A는 포인트가 2개이고 Group B도 포인트가 2개이다.
이 2개의 포인트를 모든 경우의 수로 연결한다.
- Group A 포인트 0 과 Group B 포인트 0연결 (0,0) + Group A 포인트 1 과 Group B 포인트 0연결 (1,0) = [[1,2][3,4]]
- Group A 포인트 0 과 Group B 포인트 0연결 (0,0) + Group A 포인트 1 과 Group B 포인트 1연결 (1,1) = [[1,2][3,4]]
- Group A 포인트 0 과 Group B 포인트 1연결 (0,1) + Group A 포인트 1 과 Group B 포인트 1연결 (1,1) = [[1,2][3,4]]
- Group A 포인트 0 과 Group B 포인트 1연결 (0,1) + Group A 포인트 1 과 Group B 포인트 0연결 (1,0) = [[1,2][3,4]]
이때의 코스트는 각각 4,5,6,5가 된다.
이후 연결이 되지 않은 Group B의 포인트를 더하면 된다.
- 4 + Group B 포인트 1의 최소 연결 값 2 = 6
그림과 혼동이 될 수 있는데 Group B 1 포인트의 연결 값은 2와 4 Costs중에 하나이고 가장 낮은 값인 2를 선택 한다
- 5 + 빈 Group B 포인트 없음 0 = 5
- 6 + 빈 Group B 포인트 0의 최소 연결 값 1 = 7
- 5 + 빈 Group b 포인트 없음 = 5
결과 적으로 모든 포인트 연결에 가장 작은 값은 5가 답이 된다.
이를 코드로 나타내면 다음과 같다.
if (cost.length <= row) { //모든 group a를 순환 완료한 경우 연결되지 않은 group b의 cost를 add 한다
result = 0;
for (let col = 0; col < cost[0].length; col++) { //Group b인 컬럼을 순환한다
let is = 0;
if((mask & (1 << col)) === 0) is = 1;
result += minArr[col] * (is);//broup b의 mask가 0이라면 아직 연결되지 못한 node 임으로 해당 노드에서 가장 낮은 값을 연결해 준다.
}
} else {
for(let col = 0; col < cost[0].length; col++){ //모든 group a의 경우의 수를 순환한다
// a group의 0번이 b group의 1번, 2번, 3번 과 mapping 시키고 맵핑 결과를 mask에 저장한다
result = Math.min(result, cost[row][col] + dfs(cost, minArr, row + 1, (mask | (1 << col))));
}
}- else 문이 Group A 포인트의 모든 경우의 수 처리 이고
- if 문이 Group B 포인트의 빈 경우 최소의 값 처리 이다.
상기 코드에서 2가지를 중요하게 봐야하는데,
result = Math.min(result, cost[row][col] + dfs(cost, minArr, row + 1, (mask | (1 << col))));
이 코드에서 mask 처리와
result += minArr[col] * (is);
여기에서 minArr이다.
우선 minArr는 Group B에서 빈 Point 값이 있을 때 해당 포인트에서 가장 낮은 Cost 연결 값을 갖어오는 코드이다.
이 부분에 대한 전처리는 아래와 같이 미리 수행이 필요하다.
for (let col = 0; col < cost[0].length; col++) {
for (let row = 0; row < cost.length; row++) {
minArr[col] = Math.min(minArr[col], cost[row][col]);
}
}컬럼 기준(Group B의 포인트)으로 가장 낮은 값을 미리 저장해 놓는다면 빠르게 Group B의 빈 포인트의 최소 연결값을 얻어 올 수 있다.
이제 가장 어려운 부분이 남았다. mask 처리이다.
모든 경우의 수를 처리 해야 함으로
result = Math.min(result, cost[row][col] + dfs(cost, minArr, row + 1, (mask | (1 << col))));
이 코드를 처리 할때 현재 Group A의 포인트가 어떤 Group B의 포인트와 연결 되었는지 다음 포인트로 정보를 넘겨 줘야 한다. 그래야 마지막으로 Group B의 남은 포인트를 확인 할 수 있다.
dfs(cost, minArr, row + 1, (mask | (1 << col))));
이 부분에서 row +1은 다음과 같은 의미를 갖는다.

마스크의 의미는 Group B의 어떤 점이 연결 되어있는지를 저장해서 dfs로 다음으로 넘겨주는 역할을 한다.

상기 그림처럼 Group A 0번째 포인트가 Group B 0번째 포인트와 연결이 되었음으로
다음 dfs는
dfs(cost, minArr, 0 + 1, 0 | 1 << 0) 이 되고 이는
dfs(cost, minArr, 1, 1) 과 같아진다.
이를 전체 코드로 나타내면 다음과 같다.
var connectTwoGroups = function(cost) {
let minArr = new Array(cost[0].length).fill(Infinity);
let dp = new Array(cost.length+1).fill(0).map(_=> new Array(Math.pow(2, cost[0].length)).fill(-1)); //캐슁 처리용으로 사용한다
for (let col = 0; col < cost[0].length; col++) {
for (let row = 0; row < cost.length; row++) {
minArr[col] = Math.min(minArr[col], cost[row][col]);
}
}
let result = dfs(cost, minArr, 0, 0);
return result;
function dfs(cost, minArr, row, mask) {
// console.log(row,mask.toString(2),dp[row][mask]);
if(0 < dp[row][mask]) return dp[row][mask];
let result = Infinity;
if (cost.length <= row) { //모든 group a를 순환 완료한 경우 연결되지 않은 group b의 cost를 add 한다
result = 0;
for (let col = 0; col < cost[0].length; col++) { //Group b인 컬럼을 순환한다
let is = 0;
if((mask & (1 << col)) === 0) is = 1;
result += minArr[col] * (is);//broup b의 mask가 0이라면 아직 연결되지 못한 node 임으로 해당 노드에서 가장 낮은 값을 연결해 준다.
}
} else {
for(let col = 0; col < cost[0].length; col++){ //모든 group a의 경우의 수를 순환한다
// a group의 0번이 b group의 1번, 2번, 3번 과 mapping 시키고 맵핑 결과를 mask에 저장한다
result = Math.min(result, cost[row][col] + dfs(cost, minArr, row + 1, (mask | (1 << col))));
}
}
dp[row][mask] = result; //캐슁처리
// console.log('결과', row,mask.toString(2),dp[row][mask]);
return result; //가장 낮은값
}
};
// console.log(connectTwoGroups([[15, 96], [1, 2]]));
// console.log(connectTwoGroups([[1, 3, 5], [4, 1, 1], [1, 5, 3]]));
console.log(connectTwoGroups([[54,94,80,78,26,57],[94,65,77,44,24,73],[49,49,73,32,86,3],[58,26,40,77,57,25],[41,85,16,49,91,77],[72,0,8,72,92,63],[12,88,58,5,19,34]]));
마지막으로
let dp = new Array(cost.length+1).fill(0).map(_=> new Array(Math.pow(2, cost[0].length)).fill(-1));
dp를 정의 하는데 있어서
Array(Math.pow(2, cost[0].length)
이 부분에 대해서 설명 하고자 한다.
Group B의 포인트가 3개라고 하면 Mask로 000, 111,100 등으로 표시 할 수 있다.
dsp 입장에서는 입력값으로 들어오는 Row와 Mask 값에 따라서 결과값이 달라지게 되기 때문에
Group A 포인트가 5개이고 Group B의 포인트가 3개라고 하면
- Row로 들어올 수 있는 경우의 수 6 : Group A 포인트 5개를 다 순환 하고 마지막은 6으로 넘어오게 된다.
- Mask : 최대 들어올수 있는 값은 111 = 2^3 + 2^2 + 1 = 13가지 경우의 수가 가능하다.
총 dfs에 진입 할 수 있는 경우의 수는 6 * 13가지가 가능해 진다.
- 시간 복잡도를 보자면 다음과 같다.
- Group B 최소값 처리 : row * col
- Group A 전체 순환 : row * 2^col
- Group B에서 빈칸 처리 : col
이를 합치면 row * col + (row * 2^col) * col 이 된다.
Memory 하용량은 dp로 Gruop A를 전체 순환 함으로
row * 2^col
이다.
'Problem Solving' 카테고리의 다른 글
| Largest Number (0) | 2020.09.26 |
|---|---|
| Gas Station (0) | 2020.09.24 |
| Maximum Non Negative Product in a Matrix (0) | 2020.09.20 |
| Split a String Into the Max Number of Unique Substrings (0) | 2020.09.20 |
| Rearrange Spaces Between Words (0) | 2020.09.20 |
