Maximum Number of Visible Points
Maximum Number of Visible Points - LeetCode
Level up your coding skills and quickly land a job. This is the best place to expand your knowledge and get prepared for your next interview.
leetcode.com
- 문제 내용 : 주어진 x,y 포인트에서 주어진 angle 만큼의 view 범위를 주었을 때, 해당 View범위에 담아 둘수 있는 목표 포인트의 최대 갯수는?
- 접근 방법
주어진 모든 포인트를 대상으로 각도를 만들어내고
Sorting 후 Window Sliding을 통해서 최대 포인트 갯수를 찾는다.
우선 2개의 주어진 포인트로 부터 각도를 찾아내야 한다.
이는 탄젠트를 사용하면 된다.

tanθ = 높이 / 밑변
역함수
θ = arctan(높이 / 밑변)
이걸 코드로 바꾸면 다음과 같다.
function getAngel(location, target) {
let x = target[0] - location[0];
let y = target[1] - location[1];
return Math.atan2(y, x) * 180 / Math.PI + 180;
}atan2 함수는 radian으로 결과 값이 나온다. 이를 degree로 변경해 주기 위해서
radian * (180도 / 파이)를 해주면 된다.
1π = 180도 임으로 radian으로 들어온 값을 degree로 변경 하고 위해서는 0.0174533라디안당 1도를 곱해 주면 degree 변환이 된다.
여기서 생각해 봐야 할께 Math.atan와 Math.atan2의 차이점이다.
atan의 경우 값의 표현 범위가
-π/2 ~ π/2 까지이다.
이를 그림으로 나타내면 아래와 같다.
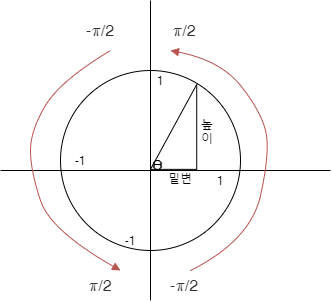
상위 내용을 code로 확인해 보면 다음과 같다.
console.log(Math.PI / 2);
console.log(Math.atan(-1/0.1));
console.log(Math.atan(-1/1));
console.log(Math.atan(-1/2));
console.log(Math.atan(0));
console.log(Math.atan(1/2));
console.log(Math.atan(1/1));
console.log(Math.atan(1/0.1));
1.5707963267948966
-1.4711276743037347
-0.7853981633974483
-0.4636476090008061
0
0.4636476090008061
0.7853981633974483
1.4711276743037347최대 범위 1.57~-1.57을 최대 최소로 해서 라디언이 결과 값으로 나오는 것을 볼 수 있다.
이를 통해서 확인 할 수 있는 것은, 제 1,4 사분면과 제 2,3사분면이 분리 되지 못한다는 것이다.
360도 전체에 대한 처리를 위해서는 arctant2를 사용 해야 한다.
arctant2의 범위는 다음과 같다

0에서 180
그리고 0에서 -180도의 범위를 갖게 됨으로써 360도를 표현 가능하게 된다.
코드로 보면 다음과 같다.
주의 해야할 것은 atan2(y, x) 라는 것이다
console.log(Math.atan2(0, -1)* 180 / Math.PI);
console.log(Math.atan2(1, 0)* 180 / Math.PI);
console.log(Math.atan2(0, 1)* 180 / Math.PI);
console.log(Math.atan2(-1, 1)* 180 / Math.PI);
console.log(Math.atan2(-1, 0)* 180 / Math.PI);
console.log(Math.atan2(-1, -1)* 180 / Math.PI);
180
90
0
-45
-90
-135상위 결과를 보면 0도에서 180도 그리고 0도에서 -135(-179도)도까지 표현 되는 것을 확인 할 수있다.
여기에 마이너스를 없애고 360도로 표현하고자 하면 +180을 더하면 된다.
console.log(Math.atan2(0, -1)* 180 / Math.PI + 180);
console.log(Math.atan2(1, 0)* 180 / Math.PI + 180);
console.log(Math.atan2(0, 1)* 180 / Math.PI + 180);
console.log(Math.atan2(-1, 1)* 180 / Math.PI + 180);
console.log(Math.atan2(-1, 0)* 180 / Math.PI + 180);
console.log(Math.atan2(-1, -1)* 180 / Math.PI + 180);
360
270
180
135
90
45tan를 이용한 각도를 구하기 위한 것이기 때문에 4분면의 회전이 0부터 360까지 연속적으로 일어나진 않는다.
이점을 유의해야 한다.
각 포인트 별 각도를 구했다면, 각도를 작은수 부터 큰수로 sorting 한 후
2회에 걸쳐서 Sliding window를 Angle 사이즈로 처리해 주면 된다.
- 2회 처리 이유는 360를 기점으로 0도로 다시 순환이 이루어지는 부분을 check해야 하기 때문이다.
전체 코드는 아래와 같다.
var visiblePoints = function(points, angle, location) {
let angles = new Array();
let universalCount = 0;
for (let point of points) {
if(point[0] === location[0] && point[1] === location[1]){
universalCount++;
continue;
}
angles.push(getAngel(location, point));
}
angles.sort((a, b) => a - b);
let getVal = (idx) => {
if (idx < angles.length) {
return angles[idx];
} else {
return angles[idx % angles.length] + 360;
}
};
let left = 0;
let result = 0;
for (let right = 0; right < angles.length * 2; right++) {
while((getVal(right) - getVal(left)) > angle) left++;
result = Math.max(result, right - left + 1);
}
return result + universalCount;
function getAngel(location, target) {
let x = target[0] - location[0];
let y = target[1] - location[1];
return Math.atan2(y, x) * 180 / Math.PI + 180;
}
};universal Count라고 하는 것이 있는데 이게 있는 이유는 location과 point의 위치가 동일한 경우가 있는데, 이 경우는 agle과 상관 없이 모두 볼수 있다고 보기 때문이다.
'Problem Solving' 카테고리의 다른 글
| Complement of Base 10 Integer (0) | 2020.10.05 |
|---|---|
| Remove Covered Intervals (0) | 2020.10.04 |
| Even Odd Tree (0) | 2020.10.04 |
| Special Array With X Elements Greater Than or Equal X (0) | 2020.10.04 |
| Minimum One Bit Operations to Make Integers Zero (2) | 2020.10.04 |
