앞서 Segment Tree를 알아 보았다.
2021.05.02 - [Problem Solving] - Segment Tree
그런데 생각보다 개발량도 많고 필요할때 바로 만들어서 쓴다는게 쉽지 않다.
그래서 Binary Indexed Tree를 알아보고자 한다.
Binary Indexed Tree는 크게 2개의 Array가 필요하다.
- N+1 Size의 오리지널 Array
- N+1 Size의 Fenwick Tree Array
오리지널 Array는 입력하고자 하는 Array 그 자체라고 생각하면된다.
[1,3,5,7,9,11,13,15]
라는 배열이 있다면 이것을
Original Array = [NA,1,3,5,7,9,11,13,15]
로 유지 하는 것이다.
NA가 들어가는 이유는 첫번째 Value를 1이라는 Index와 맞춰주기 위해서 필요하다.
다음으로 필요한것은 Fenwick Tree이다.
이 Fenwick Tree는 DP라고 생각하면 편하다.
미리 Sum을 해놓는다고 생각하면 된다.
단, 일반적인 Prefix Sum과는 차이가 있다.
우리가 생각하는 Prefix Sum은 다음과 같다.
Prefix Sum Array = [NA,1,4,9,16,25,36,49,64]
5번 6번 Index의 Sum을 찾기 위해서는
$$ 36 - 16 = 20 $$
을 사용해야 한다.
Query를 하는데 있어서는 O(1)의 속도로 해결이 된다.
그러나 Update에서 $ O(N^2) $ 이 필요하다.
예를 들어서 Index 1번의 1이라는 Value가 2로 변경 되었다고 생각해 보자.
Index 1번 이후의 모든 값들은 업데이트 되어야 한다.
만약 빈 Array에 [0,0,0,0,0,0,0,0,0] Update를 순차적으로 진행 할 경우
$$ \frac{N(N+1)}{2} $$
의 업데이트 횟수가 필요하다.
그래서 Update도 $ O(\log_2 n) $ Query도 $ O(\log_2 n) $ 이 가능한 Binary Indexed Tree가 필요하다.
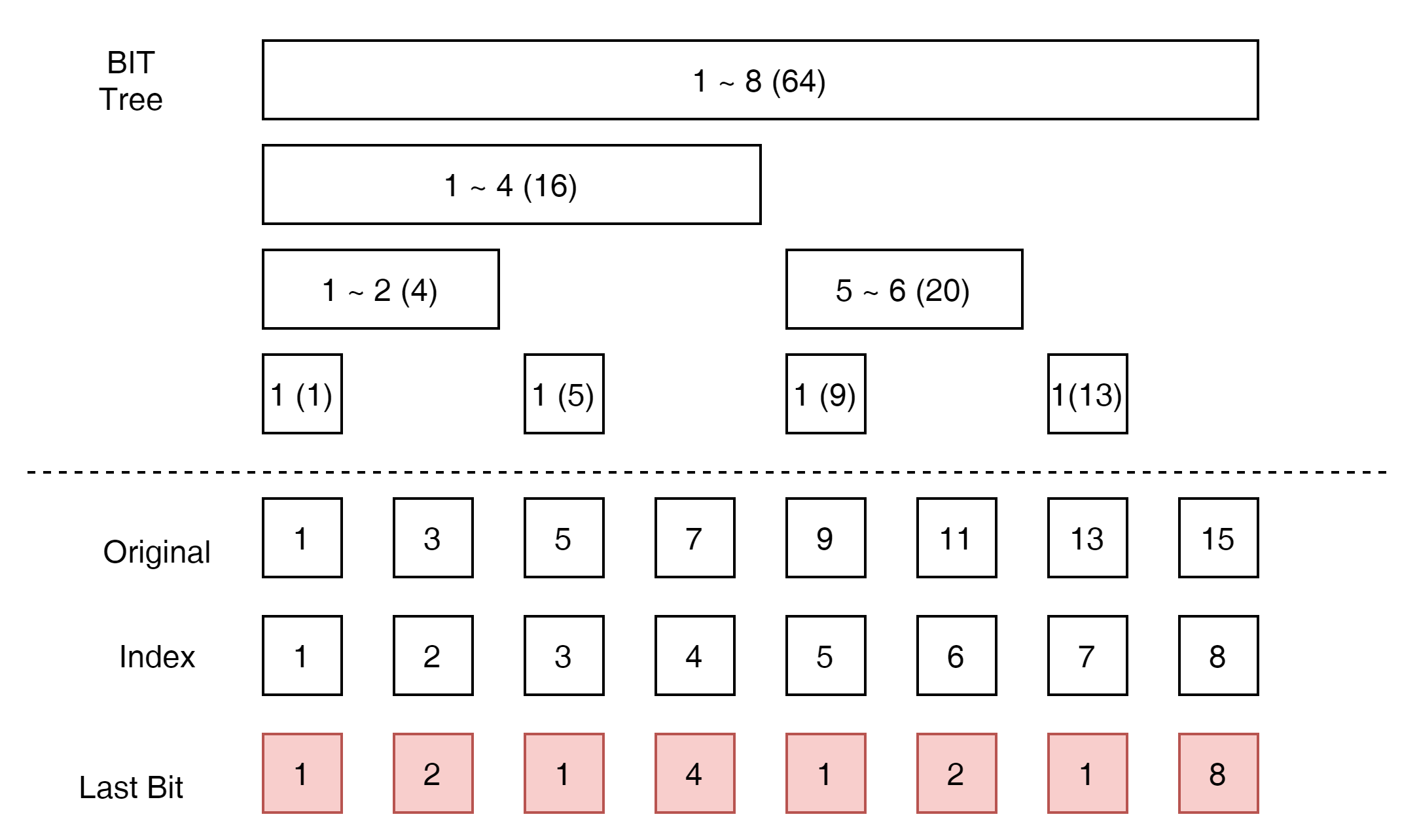
상기 그림에서 Last Bit에 대해서 알아보자
- 2의 이진수는 $ 10 $
- 3의 이진수는 $ 11 $
- 4의 이진수는 $ 100 $
- 5의 이진수는 $ 101 $
- 6의 이진수는 $ 110 $
- 7의 이진수는 $ 111 $
- 8의 이진수는 $ 1000$
이다. 이중에서 마지막 비트의 위치만을 확인 하면 Last Bit가 된다.
이 Last Bit를 상대적으로 다음과 같이 생각해 보면 된다.
1은 Original 값그대로 유지
2는 해당 Position의 바로 앞에 유지한 Original 값과 자기자신의 값 Sum
4는 상대적으로 1에서 부터 자기자신 4까지의 Sum
8은 상대적으로 1에서 부터 자기자신까지 8의 Sum이 된다.
Last Bit를 구하는 방법은 $ i & -i $ 를 사용하면 된다.
2021.05.02 - [Problem Solving] - 2진수 최 우측 1의 자리 찾아내기
이를 이용해서 Update와 query가 가능한데, 우선 Update를 알아보자.
만약 Index 1이 2로 변경된다면 다음과 같이 Update를 처리하면 된다.

Original 값 1에서 차이값이 1을 Index 1에 Plus 처리하고 해당 Index의 Last Bit인 1을 더한다.
그러면 Index 2로 그 자리를 옴기고 차이값 1을 다시 더한다.
Index 2의 라스트 값이 2를 한번 더하고 Index 4로 자리를 옮긴다.
Index 4에 + 1을 더하고 다시 라스트값 4를 더함으로써 1~8 sum을 대표하는 Index 8의 값을 65로 업데이트 한다.
절반씩 줄여서 Node를 업데이트 함으로 $ O(\log_2 n) $ 이다.
Interval Sum도 같은 방식으로 해결 가능하다.
만약 Index 1번에서 Index 7번의 Sum을 구한다고 해보자.

Index 7번의 값은 13
라스트 값인 1을 마이너스 한다.
Index 6의 값은 20
라스트 값인 2을 마이너스 한다.
Index 4의 값은 17
라스트 값인 4를 마이너스 하면 0으로 더이상 갈수 있는 곳이 없다.
모든 Sum을 하면 $ 50 = 13 + 20 + 17 $ 이 된다.
만약 1이 아닌 곳에서 부터 시작하는 Interval Sum이라고 하면 아래와 같이 2개의 Sum값을 빼주면 된다.
- Interval (7) - Interval (3)
Last Bit에 대한 알고 있다고 하면 코드는 굉장히 짧다.
var BinaryIndexedTree = (function(){
function BinaryIndexedTree (width){
this.with = width + 1;
if(width%4) this.with+=(4-(width%2));
this.origin = new Array(this.with).fill(0);
this.tree = new Array(this.with).fill(0);
}
BinaryIndexedTree.prototype.update = function(index, value){
index = index + 1; // 1 base array
let diff = value - this.origin[index];
this.origin[index] = value;
while(index < this.with){
this.tree[index] += diff;
index = index + (index & -index);
}
};
BinaryIndexedTree.prototype.prefixSum = function(index){
let sum = 0;
while(0 < index){
sum += this.tree[index];
index = index - (index & -index);
}
return sum;
};
BinaryIndexedTree.prototype.intervalSum = function (start, end) {
return this.prefixSum(end+1) - this.prefixSum(start);
};
return BinaryIndexedTree;
}
)();
'Problem Solving' 카테고리의 다른 글
| Alien Dictionary (0) | 2021.05.11 |
|---|---|
| Maximum Profit in Job Scheduling (0) | 2021.05.06 |
| 2진수 최 우측 1의 자리 찾아내기 (0) | 2021.05.02 |
| Segment Tree (0) | 2021.05.02 |
| Create Sorted Array through Instructions (0) | 2021.05.02 |
