Shortest Path Visiting All Nodes
문제 내용
주어진 Node를 모두 Visite하는데 얼마의 step이 필요한가?
각 Node는 중복으로 방문이 가능하다.
접근 방법
개인적으로 이해하는데 시간을 오래 끌었다.
Youtube나 google을 조회해 봐도
Floyd-Warshall 알고리즘이나 Dijkstra 를 이용한 방법이 검색되었다.
한마디로 이해하기 어렵고 주어진 시간내에 개발하기도 어려웠다.
그래서 Discussion을 찾아보는데 Smart BFS를 사용한 방법으로 본 문제를 풀었다는 이야기를 많이 보았다.
그래서 여기서 말하는 Smart BFS가 무었인지 알아보고 이를 통해서 문제를 풀어보고자 한다.
BFS 접근 방법
BFS는 queue를 이용해서 접근 범위를 넓혀가는 방식이다.
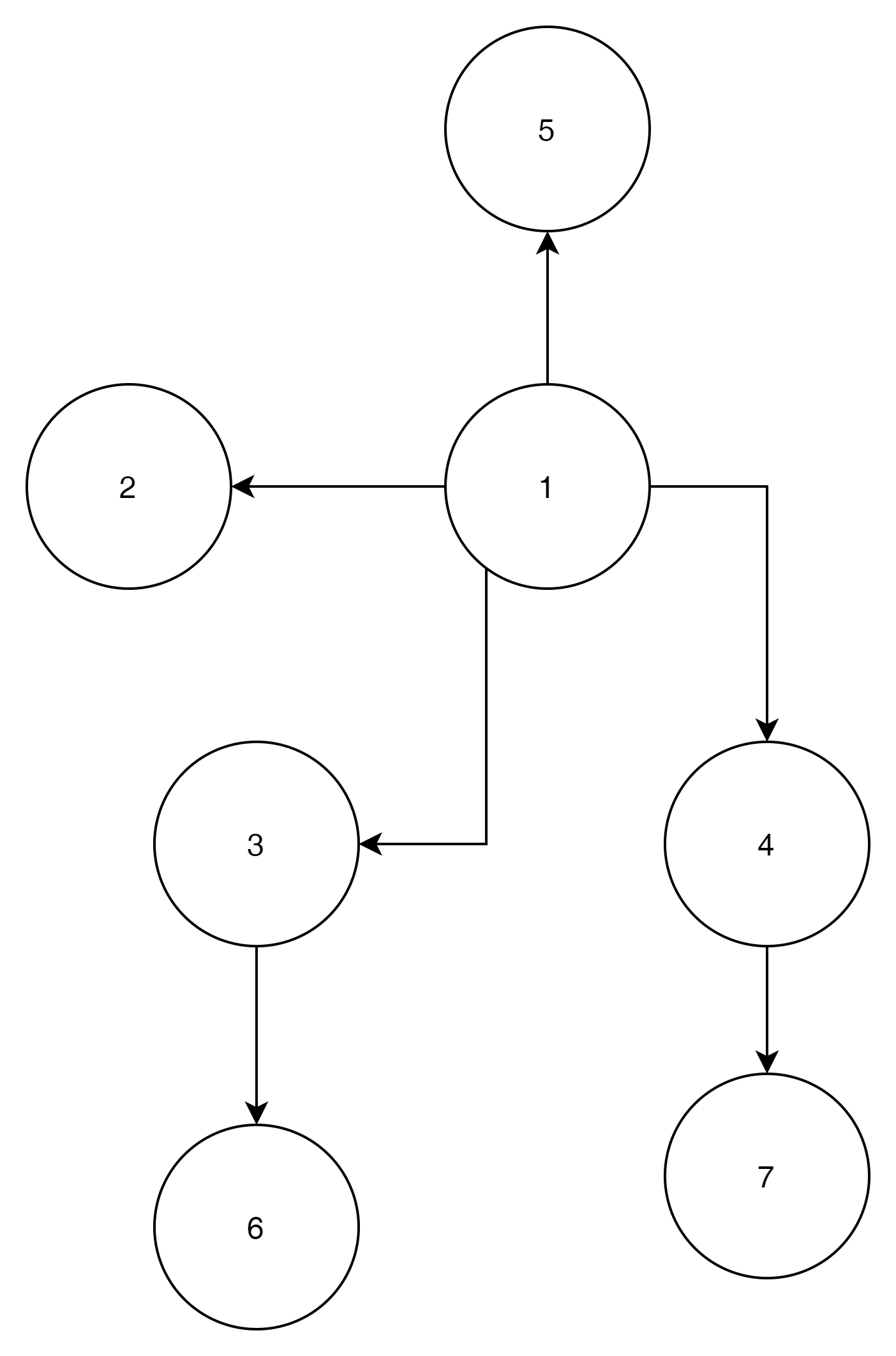
이런 문제가 주어졌고 1번 노드를 중심으로 해서 BFS를 접근하면 아래의 순서로 BFS를 처리하게 된다.

- 1번 Node를 Queue에 담는다
- while 문에서 Queue의 length를 확인한다
- Queue의 길이만큼 Node를 뺀다
- 여기서는 1 하나임으로 1 Node만 뺀다
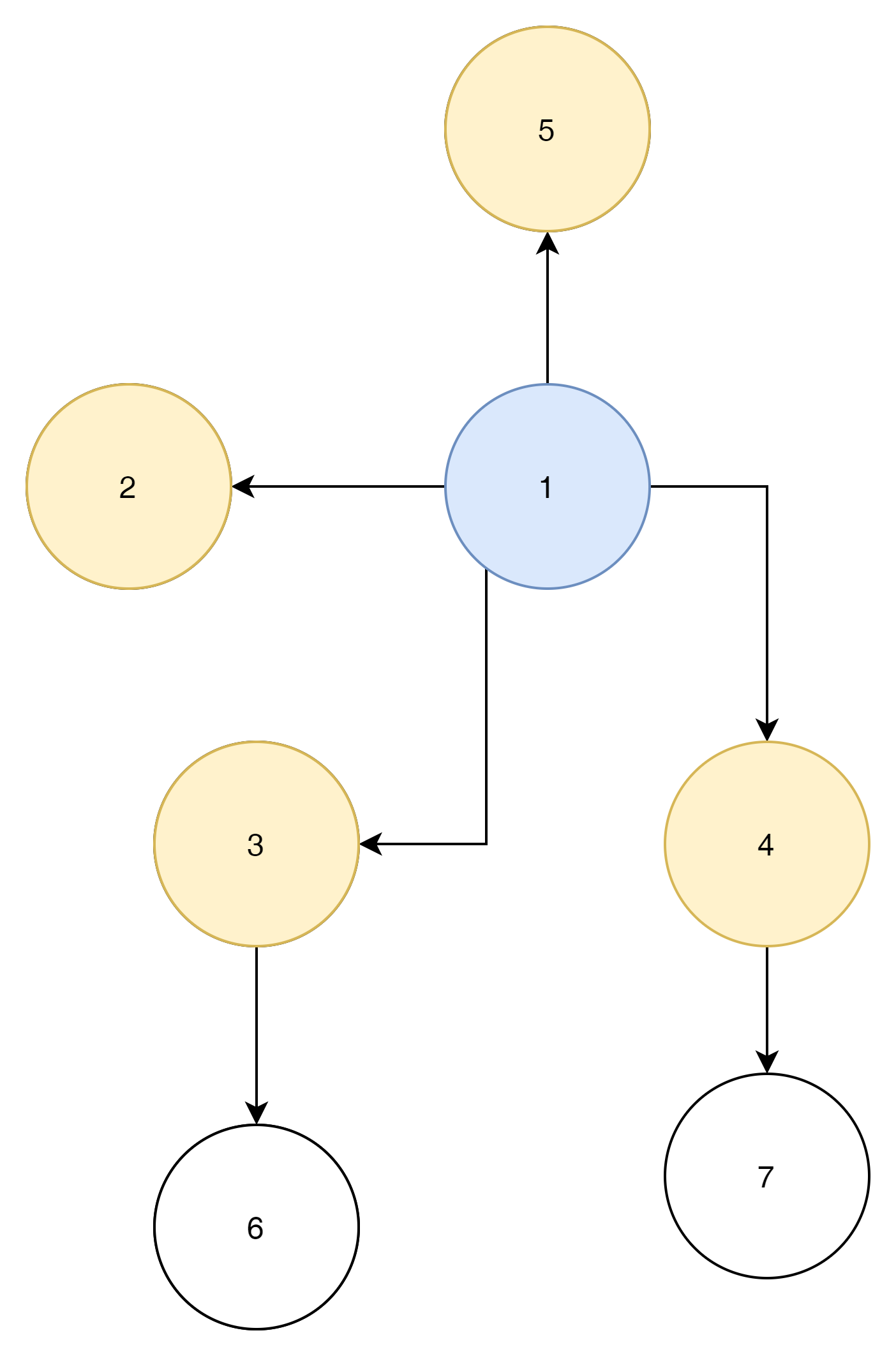
- 1 Node에서 근접한 Node를 Queue에 담는다 ->2,3,4,5 번 Nodes를 큐에 담는다
- while 문에서 Queue의 length를 확인한다
- Queue의 길이만큼 Node를 뺀다
- 2번 Node -> child 없다
- 3번 Node -> 6번 Node를 담는다
- 4번 Node -> 7번 Node를 담는다
- 5번 Node -> child 없다

- while 문에서 Queue의 length를 확인한다
- Queue의 길이만큼 Node를 뺀다
- 여기서는 6번 7번 Node를 뺀다
- 6번 Node -> child 없다
- 7번 Node -> child 없다
- while 문에서 Queue의 length를 확인한다
- Queue가 비었음으로 종료한다.
위의 경우는 모두 4번의 while을 통해서 모든 Node를 순회 하였다.
이를 통해 알 수 있는 것은
- Node의 깊이는 4 depth이다
- Node는 7개로 이루어져 있다.
그러나 Path를 확인할 수는 없다.
그 path가 얼마나 길지 또는 짧을지 알 수 없다.
알기위해서는 모든 경우의 수를 확인하는 방법 밖에는 없다.
Smart BFS 접근
1이 시작점이라고 가정하자.

1에서 선택할 수 있는 Node는 2,3,4,5가 된다. 이중 어디를 선택하든 각각의 Path는 독립적이다.

각각이 독립적인 Path임으로 위의 Path는 모두 각가의 상태를 저장할 수있다.
예를 들자면 visited로 나타낼 수 있다.
가장 쉬운 Mask를 사용해서 이를 처리하자.
2021.09.12 - [Problem Solving] - Masking을 활용한 DP 문제 풀기 (Partition to K Equal Sum Subsets)
Mask 활용 법은 위를 참고하자.
위의 4가지 Case는 모두 한가지의 상태로 시작했다.
(0번째 index를 1번 Node라고 하겠다.)
'1111111' -> '1111110'
1번 Node(0번 Index)를 무조건 visited한 상태가 된다.
이 상태에서 위의 4가지는 각각의 상태로 전이된다.
맨 좌측 부터 Node와 Status를 표시하면,
5 '1101110', 2 '1111100', 3 '1111010', 4 '1110110'
이런 상태를 갖게 된다.
이 상태에서 각각의 노드는 다시 선택을 하게 된다. (위에 그림을 잘못 그렸는데 무방향성 그래프이다)

맨 좌측은 5번에서 1번 노드를 선택해야 한다.
1번 노드는 2번을 3번 노드는 1번아니면 6번을, 4번 노드는 7번 아니면 1번을 선택해야 한다.
여기서 일반적인 BFS와 다른점이 나타나는데, 한번 visited한 Node를 다시 또 접근한다는 것이다.
모든 Node를 순회해야 하기때문에, 어쩔수 없이 돌아와야 한다.
- 이 때문에 순환이 발생하게 된다. -> DFS를 쉽게 사용할 수 없는 이유가 된다.
그럼 어떻게 visited를 check 해야하는지 좀더 알아보자.
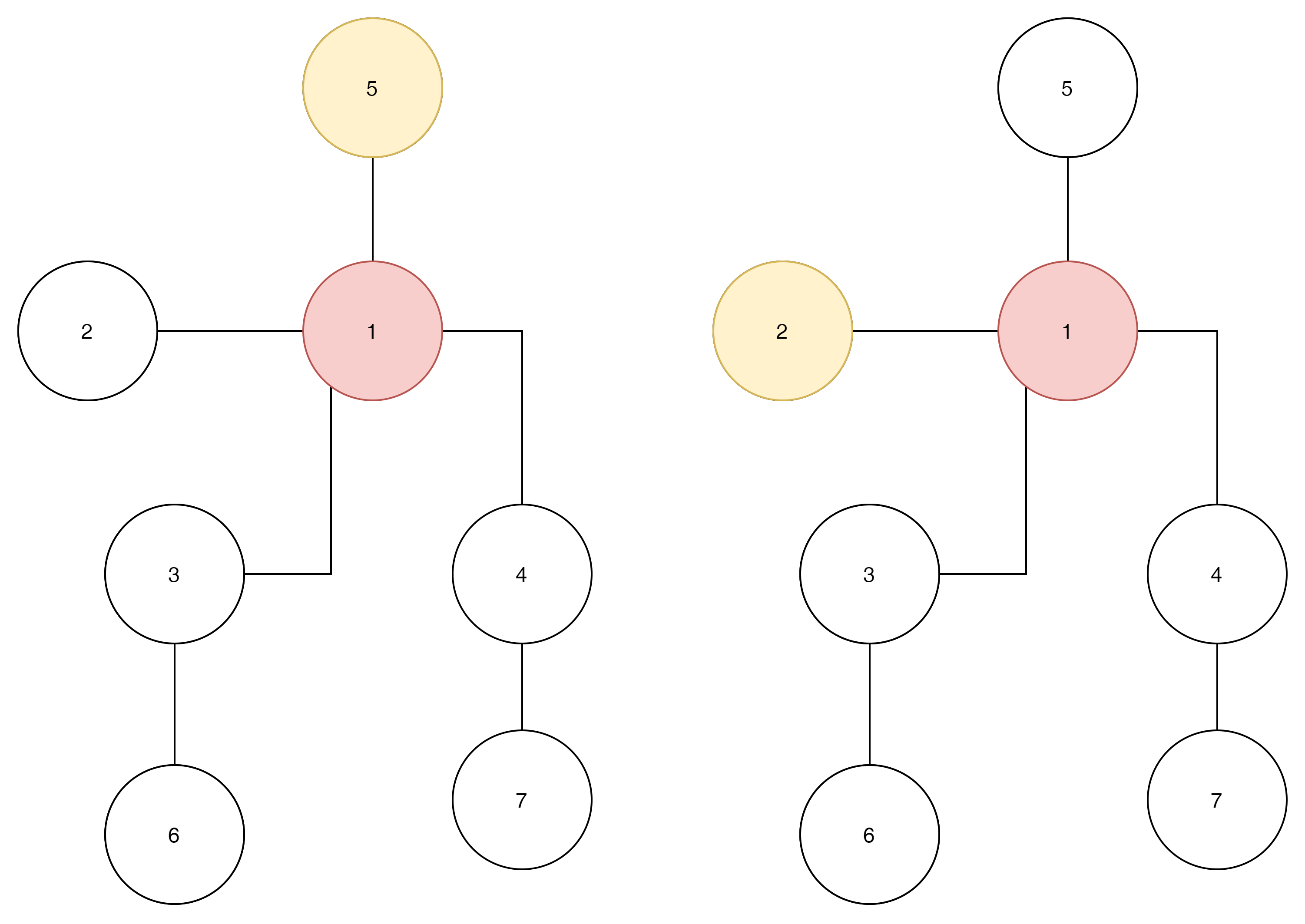
맨 좌측 두개만을 대상으로 각각 [1번 노드, 5번노드, 1번노드], [1번노드, 2번노드, 1번노드]를 선택했다고 생각해보자.
이경우 mask는 1 '1101110', 1 '1111100' 가 된다. 비록 다시 1로 돌아 왔지만 mask는 변화가 없다. 변한것은 현재 노드번호와 mask의 관계이다.
즉 1번 노드를 선택했을 때, '1101110' / '1111100' 이렇게 서로 다른 상태를 갖는 상태가 된다는 것이다.
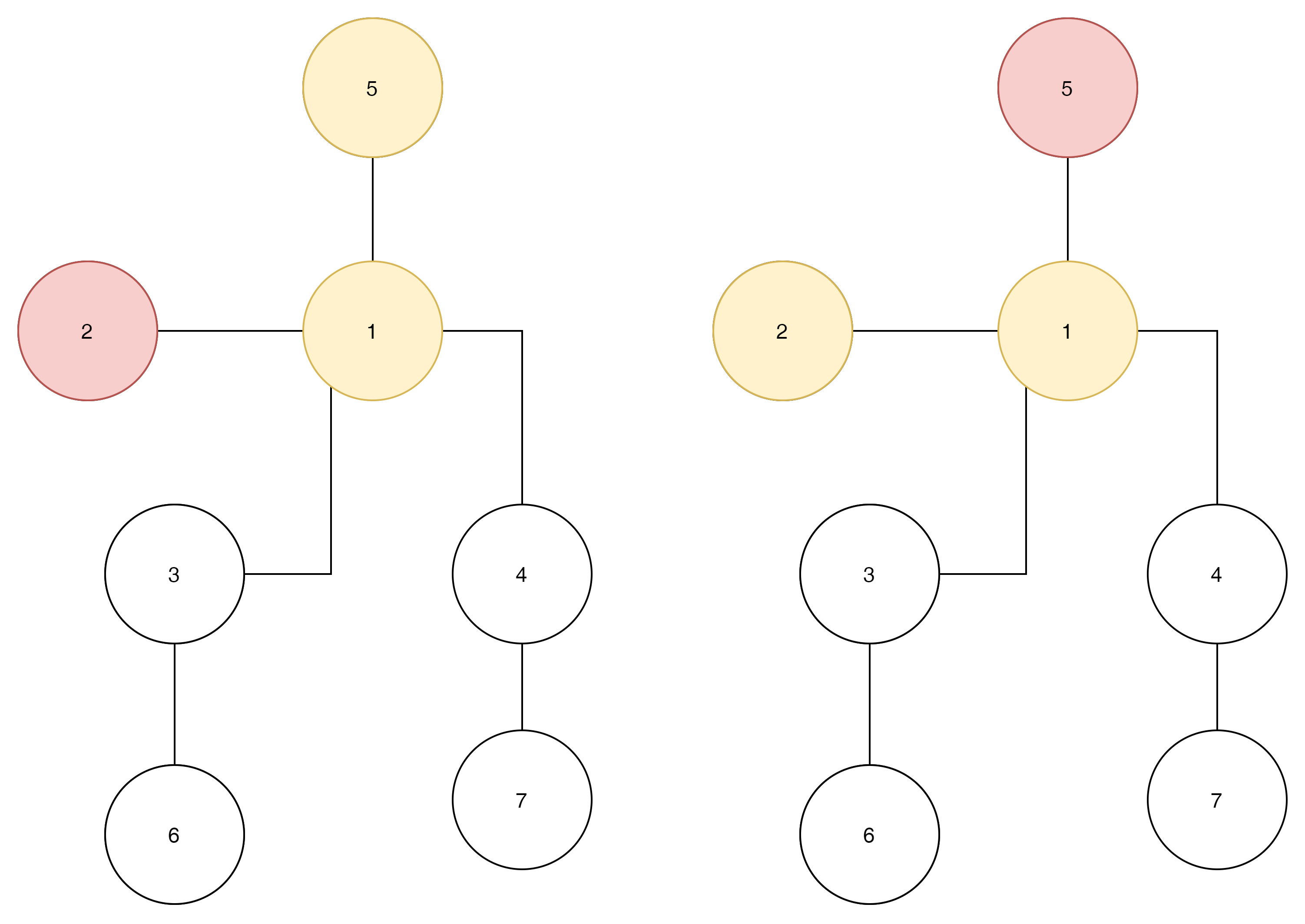
그럼 이제부터는 Node와 Mask를 같이 쌍으로 visit를 관리한다고 생각해 보자.
왼쪽은
1 '1111110'
5 '1101110'
1 '1101110'
을
오른쪽은
1 '1111110'
2 '1111100'
1 '1111100'
를 visited로 관리하게 된다.
같은 1번 node라고 해도 완전히 다른 상태가 된다는 것을 알 수 있다.
둘다 1번 노드 상태라고 생각해 보자.
왼쪽 1번 노드 상태에서 다시 5번 노드를 접근가능할까?
아니다 왜냐하면 이미 "5 '1101110'" 5번 노드에서 1번과 5번 노드 mask 가 visited되었음을 나타내고 있기 때문이다.
그래서 왼쪽은 2번, 3번, 4번의 선택사항이 있다.
이런 의문이 있을 수 있다. 오른쪽에서 이미 3번을 visited했는데?
맞다 하지만 mask가 서로 다르다.
- 왼쪽의 2번 노드 마스크 : 2 '1101100'
- 오른쪽의 2번 노드 마스크 : 2 '1111100'
이와 같은 방식을 통해서 좌측과 우측이 서로 충돌하지 않고 각가의 path를 갈 수 있다.
그럼 아래의 경우는 어떻게 될가?

왼쪽과 오른쪽 모두 2번노드와 5번 노드를 visit 하고 1번 노드로 와있다면?
- 왼쪽의 1번 노드 마스크 : 1 '1101100'
- 오른쪽의 1번 노드 마스크 : 1 '1101100'
위의 2노드는 같게 된다. 둘중에 하나만 남기고 계산을 이어가면 된다.

여기서는 다시 3번 혹은 4번 노드를 선택하는 것으로 분기해서 2가지 Path가 만들어 질수 있다.
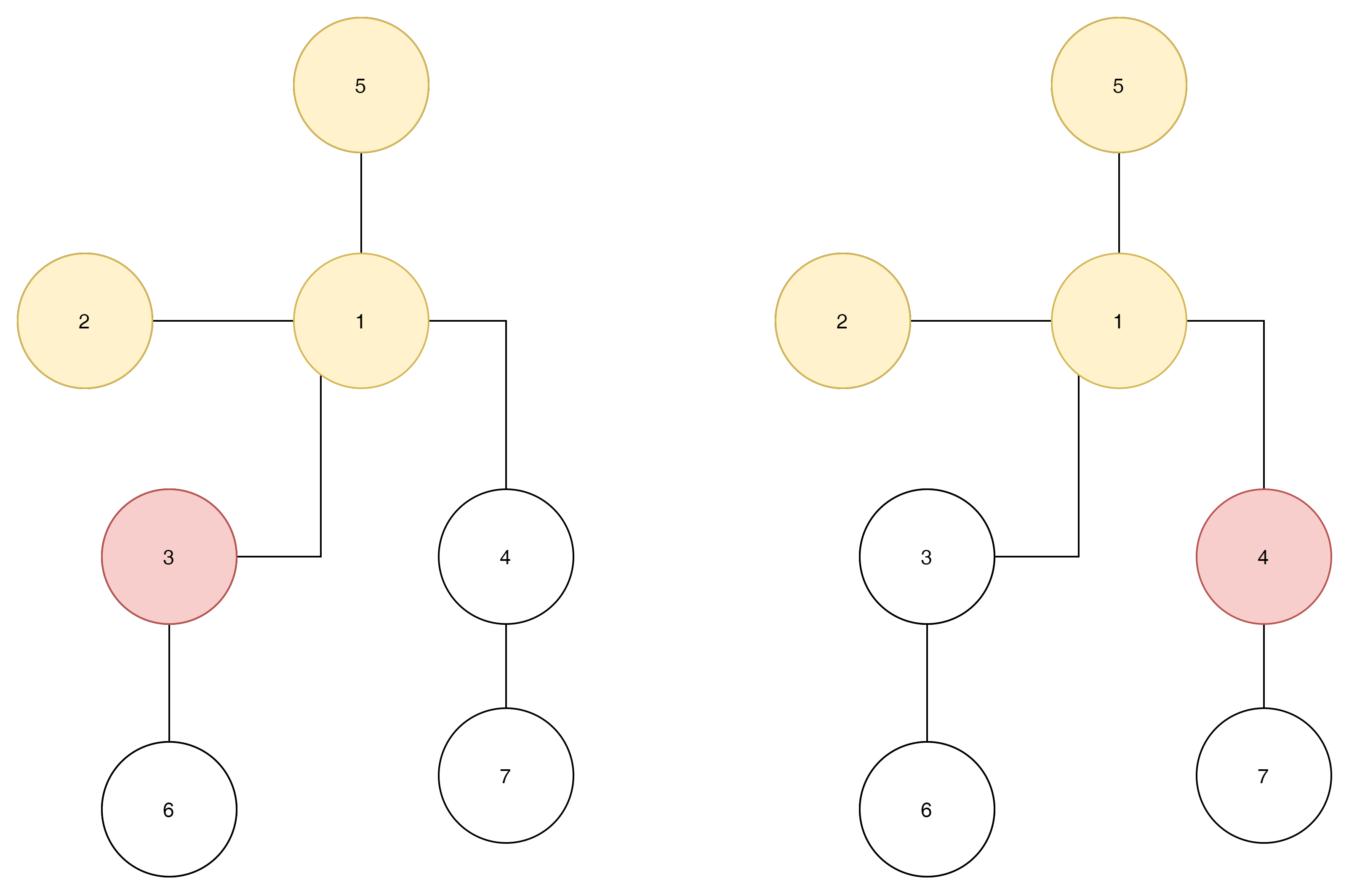
이런방식으로 각각의 Node가 전이되는 Count(step)을 계산하다가, 하나의 Path라도 mask가 0이 되면 계산을 종료하고 해당 count값을 return하면된다.
여기서 mask 0을 따지는 이유는 mask가 0이 될때 모든 node가 순환했다는 것을 말할 수 있기 때문이다.
위의 설명은 1번 node가 시작점이라고 정해줬는데, 실제 문제에서는 이 시작점이 정해져 있지 않다.
- 모든 Node를 시작점으로 위의 path순환을 모두 진행해야 한다. (완전검색)
코드 분석
설명이 난잡한데, 깔끔하게 설명하기가 쉽지 않다.
코드를 설명하는 것으로 말하고자 하는 의도를 보완하고자 한다.
var shortestPathLength = function(graph) {
let queue = new Array();
let dp = new Map();
const targetMask = (1 << graph.length) - 1;
for (let i = 0; i < graph.length; i++) {
let mask = targetMask ^ (1 << i);
queue.push([i, mask]);
dp.set(`${i}_${mask}`, true);
}
let count = 0;
while (0 < queue.length) {
let len = queue.length;
for (let i = 0; i < len; i++) {
const [position, mask] = queue.shift();
if(mask === 0) return count;
for(let next of graph[position]){
let nextMask = mask & (1 << next) ? mask ^ (1 << next) : mask;
if(dp.has(`${next}_${nextMask}`)) continue;
dp.set(`${next}_${nextMask}`, true);
queue.push([next, nextMask]);
}
}
count++;
}
return count;
};
full code는 위와 같다.
우선 시작하고자하는 모든 node를 큐에 담는다.
그와 관련된 상태도 큐에 담자.
- dp의 key는 "node 번호 _ 마스크" 이다.
물론 node array에 map을 이용해서 mask를 dp할 수도 있지만 설명하기 직관적이어서 이렇게 작성했다.
for (let i = 0; i < graph.length; i++) {
let mask = targetMask ^ (1 << i);
queue.push([i, mask]);
dp.set(`${i}_${mask}`, true);
}
모든 경우의 수의 seed points를 큐에 넣었다. 이제 이 큐를 빼서 path를 진행 시켜야 한다.
while (0 < queue.length) {
let len = queue.length;
for (let i = 0; i < len; i++) {
......
}
count++;
}while을 통해서 queue가 비었는지 확인하고, empty가 아닌 경우에만 while을 실행한다.
bfs이기때문에 들어온 queue의 값이 모두 소진될때까지 for문을 돌리자.
이때 queue는 하나의 node의 상태전이를 뜻함으로 count를 하나씩 늘려간다.
count의 위치가 중요한다. for문 안에서 queue가 소진될때 node를 visit한다고 생각하기 때문에, 꼭 count는 for이후에 위치시켜야 한다.
이 부분에서 오해를 하면 안되는데

이와같은 bfs방식으로 depth를 알고자 하는 것이아니다.

위와 같이 어떤 node에서 파생된 독립된 다음 node 상태를 한 단계씩 쫒아가는 방식이다.
- 여기에서 count는 node하나에서 다음 node로 한칸 욺직인 것을 나타내는 것이다.
for (let i = 0; i < len; i++) {
const [position, mask] = queue.shift();
if(mask === 0) return count;
for(let next of graph[position]){
let nextMask = mask & (1 << next) ? mask ^ (1 << next) : mask;
if(dp.has(`${next}_${nextMask}`)) continue;
dp.set(`${next}_${nextMask}`, true);
queue.push([next, nextMask]);
}
}이제 queue에서 node를 하나 갖어와서 다음 next로 갈수있는 node를 찾는다.
이미 node번호와 mask가 visited되었다면 다른 path가 이미 선점한 것으로, 본 노드를 통한 path진행은 의미가 없다. 큐에 push를 하지않고 끝낸다.
만약에 다음 node가 visited된적이 없는 mask를 갖고 있다면 큐에 push한다.
마지막으로 mask가 가장먼저 0을 만나게 되면,
const [position, mask] = queue.shift();
if(mask === 0) return count;더이상 path를 진행 시키는 것이 무의미 함으로 현재에서 종료한다.
Time Complexity는 쉽게 떠오르지 않는데, 다른 틀리더라도 남겨보고자 한다.
Node의 Path를 뽑을 수 있는 경우의 수는 factorial이 될것 같다.
3개의 node가 있을때,
첫번째 node 선택 수는 3번째 선택 노드 수는 3번, 다음은 2번, 1번 임으로
1,2,3
1,3,2
2,1,3
2,3,1
3,1,2
3,2,1
$ 3! = 6 $ 가지 경우의 수가 나온다.
물론 동일 노드를 한번더 접근이 가능함으로 (예를 들자면 1 -> 2 -> 1 이런식으로 되돌아 오는 경우가 있을 수 있음. 하지만 한번 하고 나면 다시는 못함)
$ O(Node! * 2) $의 time complexity가 생기는것으로 생각이 든다.
물론 이것을 masking 방식으로 계산하면 또 다른 방식으로 가능할 수 있다.
만들어낼 수 있는 최대 path길이를 Node * 2라고 하면, 이 길이만큼 11111 <- 이럼 masking이 생길 것이고 이 masking은 선택하고나 미선택 하는 방식으로 $ O(2^{Node * 2}) $ 으로 나타낼 수 있을 것 같기도 하다.
혹시 정확히 하시는 분을 알려주세요. 모르겠네요 ㅎㅎㅎ
'Problem Solving' 카테고리의 다른 글
| Decode Ways (0) | 2021.09.22 |
|---|---|
| Arithmetic Slices (0) | 2021.09.22 |
| Masking을 활용한 DP 문제 풀기 (Partition to K Equal Sum Subsets) (0) | 2021.09.12 |
| Jump Game II (0) | 2021.08.30 |
| Sparse Matrix Multiplication (0) | 2021.08.17 |
