문제 내용
주어진 숫자 Array가 있다.
해당 Array index 0에서 출발한다고 할때, Jump가 가능한 범위는 arr[i]라고 할 수 있다.
예를 들어 arr[0]이 3이면 arr[1], arr[2], arr[3]으로 자리를 옮길 수 있게 된다.
Array의 마지막 Index까지 갈수 있는 최소의 Jump 횟수를 구하시오.
접근 방법
DP를 이용해서 문제를 풀면 된다.
그런데 이렇게 간단히 최적화 되는 문제가 아니다 보니 글을 남기게 되었다.
DP로 접근하고 이후 Greedy로 접근해 보겠다.
DP 접근
다음과 같은 문제가 주어졌다고 생각해 보겠다.
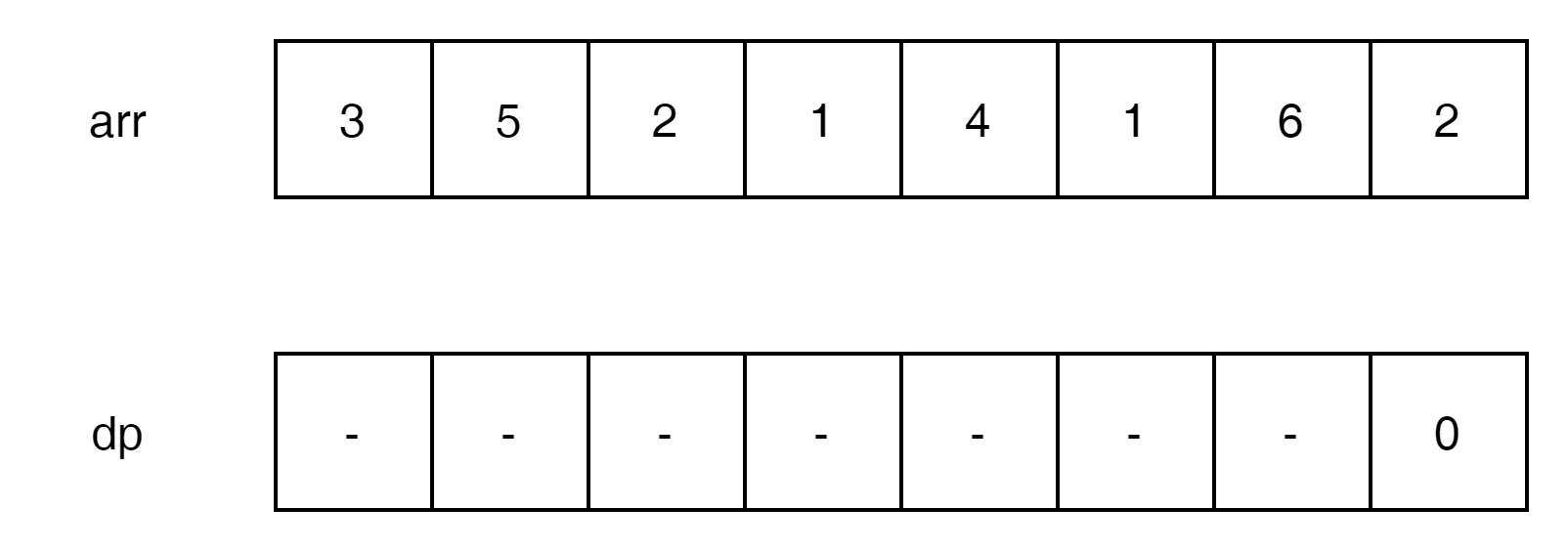
dp는 현재 index에서 마지막 index 7인 '2'까지 최소한의 jump를 기록 한다고 정의하자.
뒤에서 부터 접근해 보겠다.
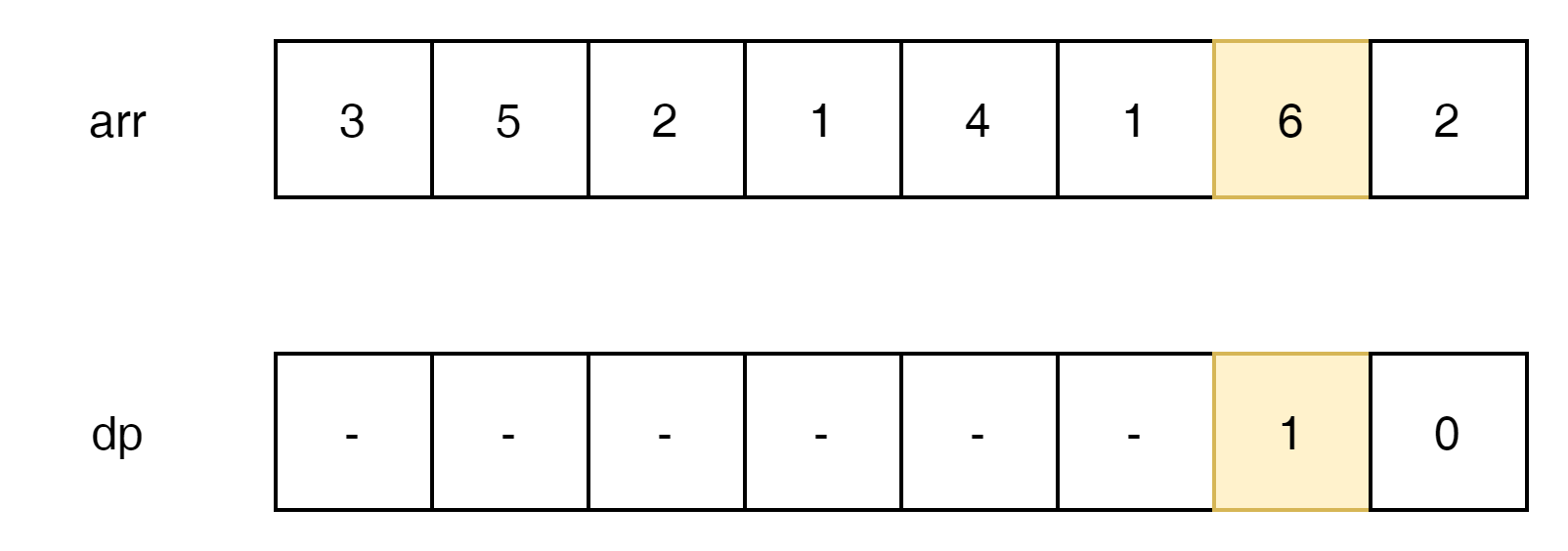
6 index는 1번의 jump로 접근 가능하다.

5번 index는 6으로 한번 Jump해야함으로 2가 된다.

4번 index는 바로 접근 가능함으로 1번
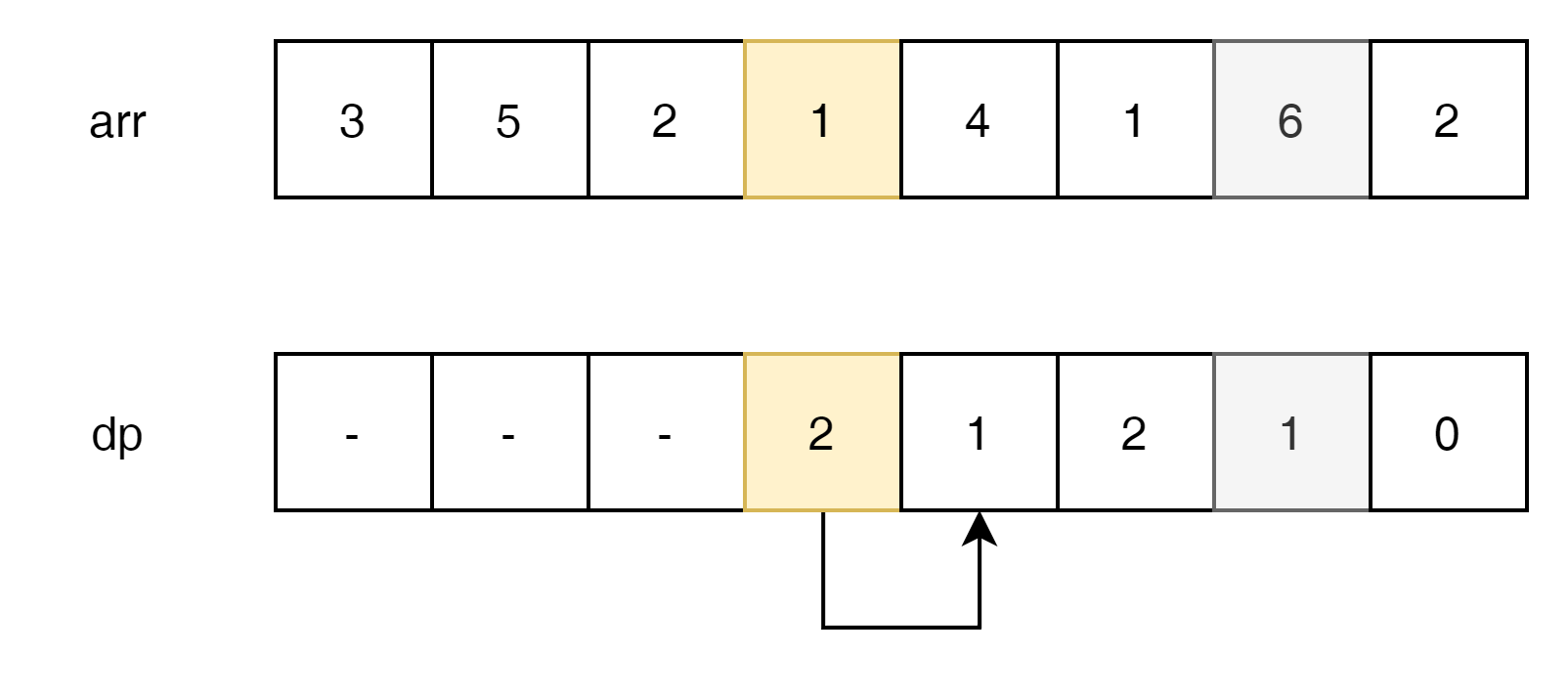
같은 방식으로 계속 해보겠다.
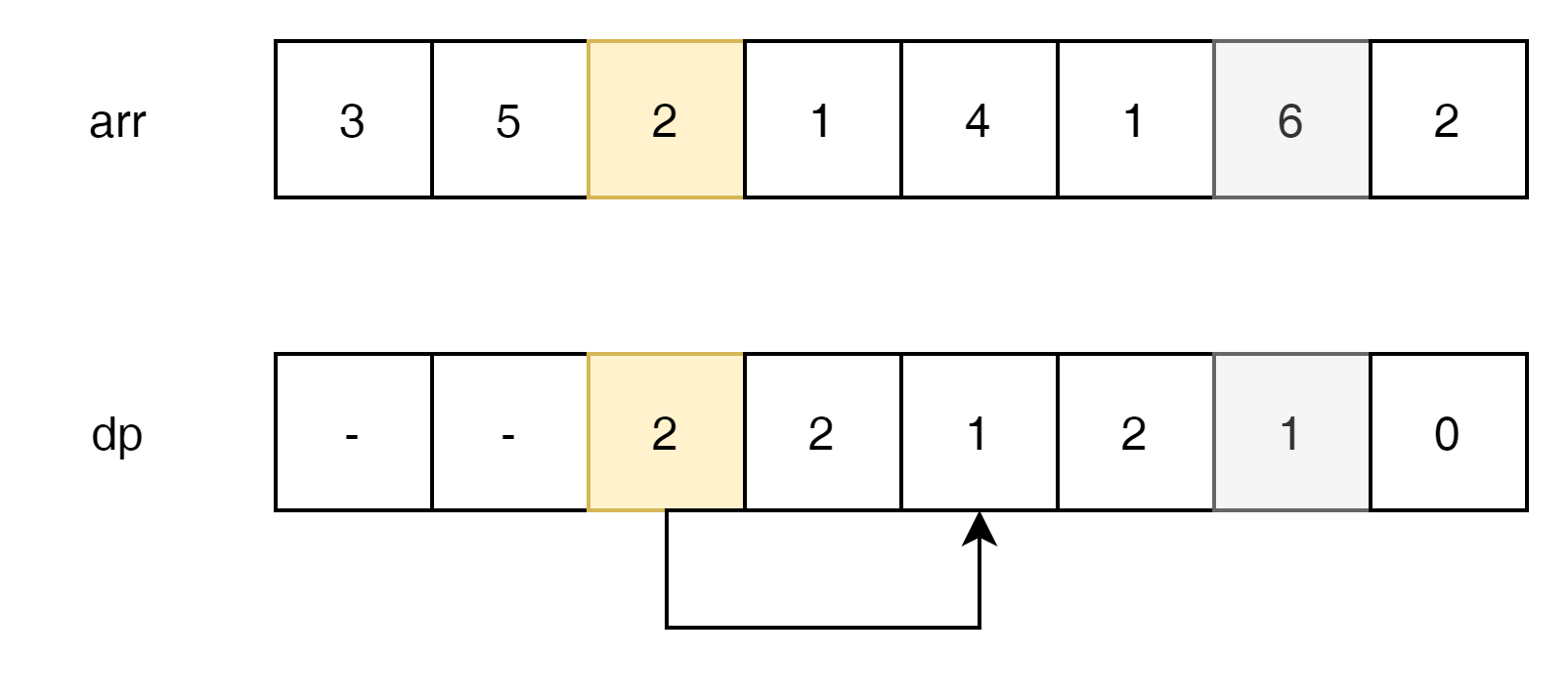
2번 index는 3번과 4번중에 선택 가능한데, 가장 작은 jump를 갖는 4번 index를 선택했다.
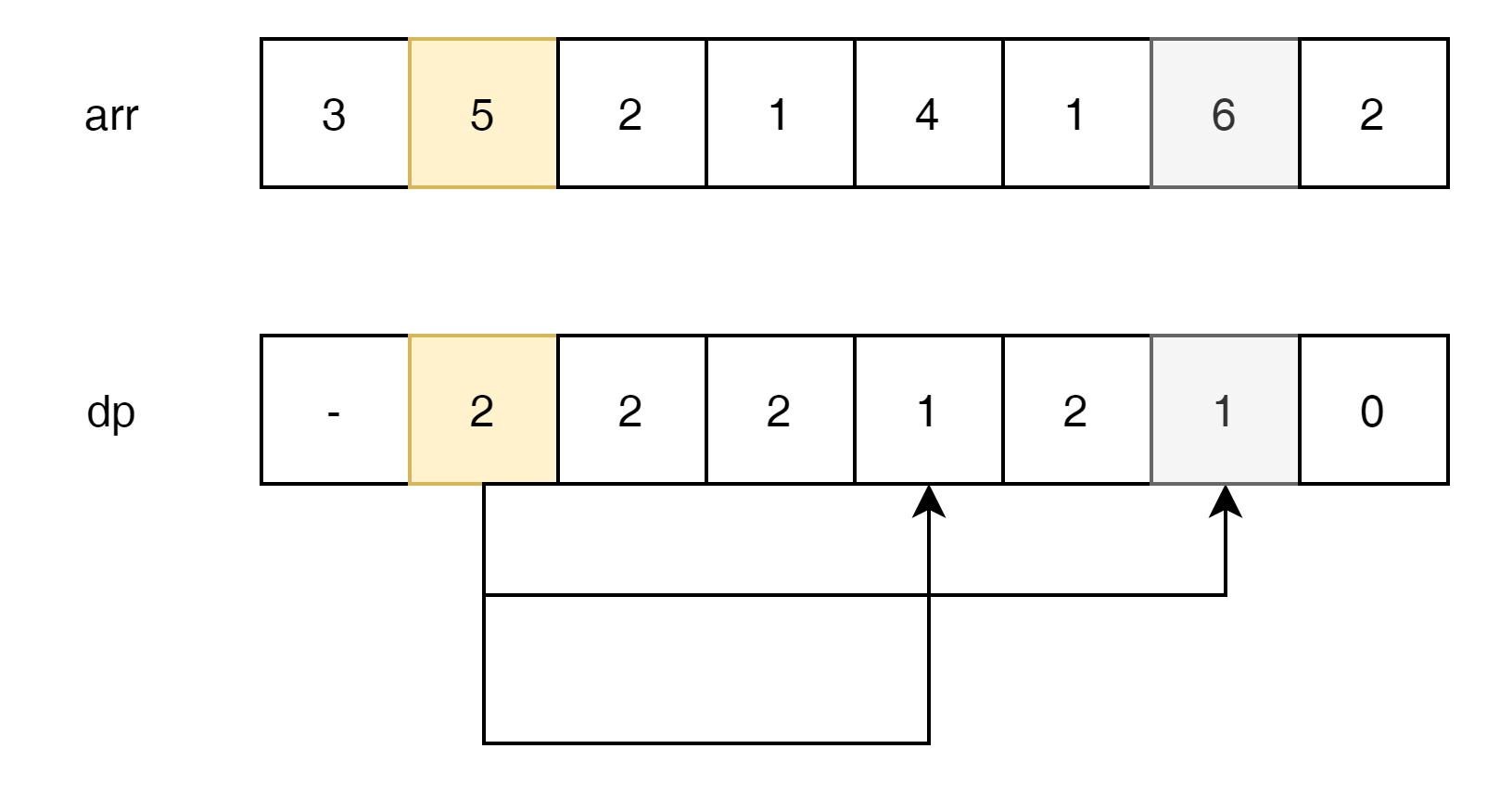
1번 index는 4번과 6번 아무것이나 선택 가능하다.

최종적으로 0번 index는 jump 2를 골라야 함으로 3이 답이된다.
이 행위를 0번에서 부터 end index가지 dfs search를 하게 되면 아래와 같다.
class Solution:
def canJump(self, nums: List[int]) -> bool:
@lru_cache(None)
def helper(position, move):
print(position, move)
if position == (len(nums) - 1): return True
if len(nums) <= position: return False
for idx in range(position + 1,position + move + 1):
if helper(idx, nums[idx]):
return True
return False
return helper(0, nums[0])복잡도는 $ O(N^2) $이 된다.
그 이유는 하나의 index에서 길이만큼 오른쪽을 search해야 하는데 최악의 경우
4,3,2,1,0 <- 이런식으로 두번 search가 가능하기 때문이다.
Greedy 접근
이 접근때문에 본 글을 쓰게 되었다.
처음에 아무리 봐도 이게 무슨 말이 안되는 방법인가 싶었는데, 한참 두고 보니 말이 되고 논리가 되는 듯 해서 적어 본다.

Farthest Range라는 개념을 설명하고자 한다.
가정 먼저 시작하는
- index 0는 무조건 접근해야하는 선택가능한 범위이다. 이것은 피할 수 없다.
이 Range의 범위는 자기 자신으로 끝나게 된다.
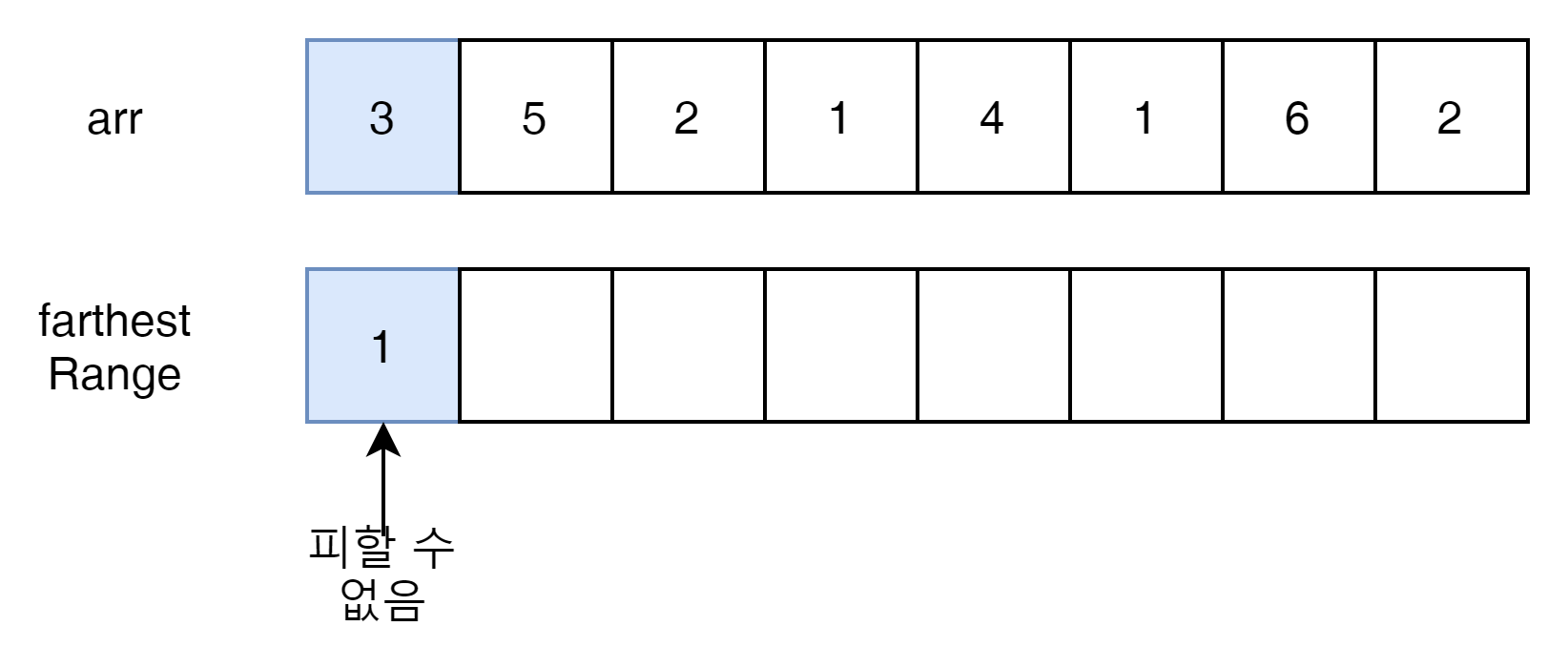
그럼 다음 Move는 어디에서 이루어질까?

1번, 2번, 3번 index의 range는 역시 피할 수 없다.
위의 어떤 값을 선택하든 2번째 Jump를 이 녹색안에서 일어나야 한다는것은 명확하다.

그럼 3번째 Range는 어디가 될까?

5로 인해서 5,6,7번 index가 선택 되게 된다. 2번 1번 index도 해당 범위 내임으로 변하는 것은 없다.
이제 피할 수 없는 jump의 위치는 어디인가?
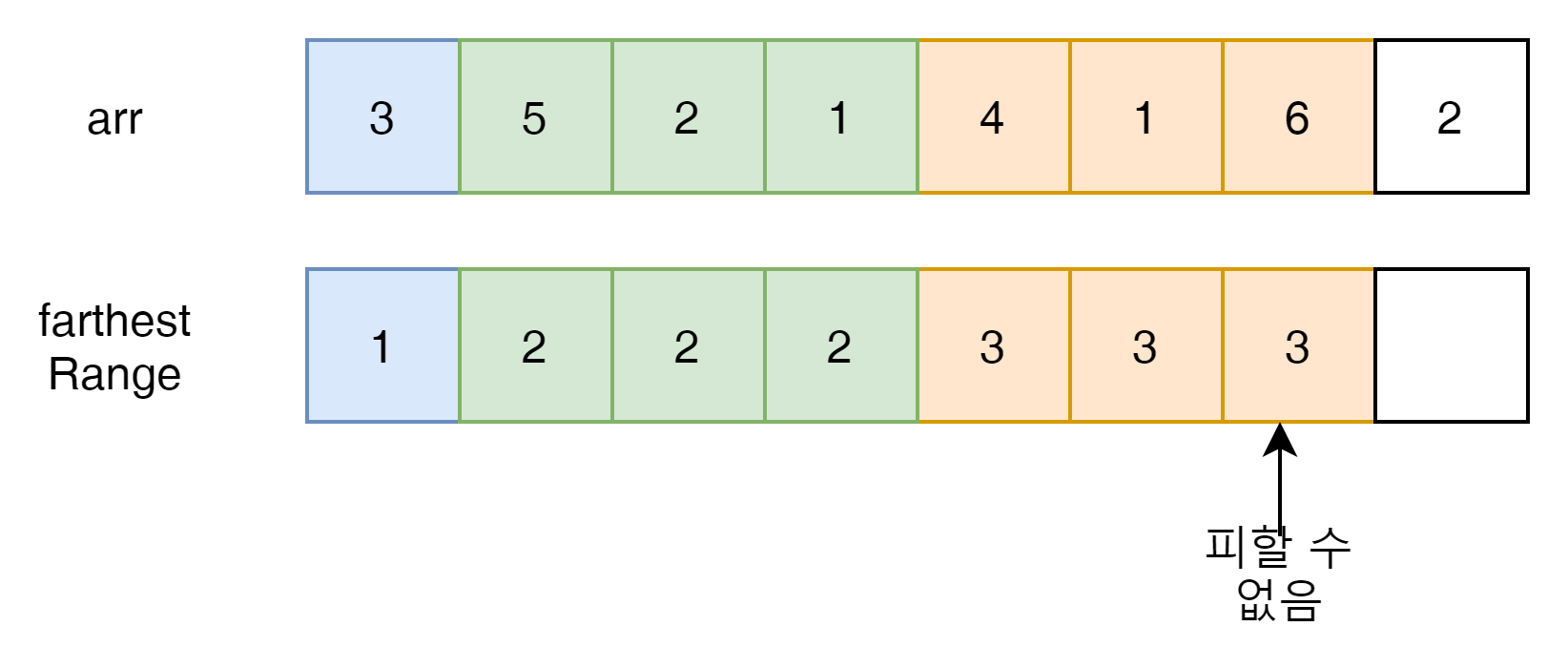
3번째 jump는 어떤한 경우에라도 통과해야 한다.
마지막 index는 jump의 횟수에 넣을 필요 없음으로

최소 jump 횟수는 3이된다.
이러한 Range 방식의 Greedy가 가능한 이유는 전제사항에
- 반듯이 end에 접근할 수 있다
라는 전제가 있기 때문에 가능하다.
물론 다음 Range 범위가 1 이상 늘어나지 않는다면 false처리 하는 방법도 있을꺼 같긴 하다.
class Solution:
def canJump(self, nums:List[int]) -> bool:
lastIdx = len(nums) - 1
for i in range(len(nums)-1, -1, -1):
if lastIdx <= i + nums[i] :
lastIdx = i
return True if lastIdx == 0 else False복잡도는 $ O(N) $ 이 된다.
'Problem Solving' 카테고리의 다른 글
| Shortest Path Visiting All Nodes (0) | 2021.09.16 |
|---|---|
| Masking을 활용한 DP 문제 풀기 (Partition to K Equal Sum Subsets) (0) | 2021.09.12 |
| Sparse Matrix Multiplication (0) | 2021.08.17 |
| Javascript 32bit 이상 Number&Integer 계산하기 (BigInt) (1) | 2021.08.14 |
| Longest Repeating Character Replacement (0) | 2021.08.13 |
