문제 내용
주어진 m x n 문자 배열이 있고, Dictionary가 주어진다면 해당 문자배열에서 조합가능한 모든 Dictionary내 words를 찾아라.
접근 방법
이런 board가 주어 졌다고 생각해 보자

가장 쉬운 접근 방법은 하나씩 조회해 보는 것일것 같다.
가령 'o'가 있이니까 Dictionary내에서 'o'가 있는 모든 words를 1회 search한다.
그리고 다음으로 a또는 e로 이동한다. 다시 앞서 조회된 o의 words에서 a또는 e가 있는 words를 찾는다.
이렇게 찾다가 words의 마지막 char와 board의 char가 동일해지는 순간 결과 값으로 등록 하면 된다.
그리고 다시 (0,1)인 'a'부터 다시 조회를 시작하면 된다.
이 방법을 최악의 경우로 가정해 본다고 한다면 모든 board는 'a'로 이루어져 있고 $$ [a,aa,aa,aaa,aaaaa ..... a^n] $$ 으로 이루어 져있다고 생각하면 board는 한 cell당 $$ a^n $$ 길이 또는 $$ m x n $$ 길이만큼 모든 모드를 계산하게 된다.
그래서 생각되는 시간복잡도는 $$ O( m*n^{max(a^n, mxn)} $$ 이 될 것이다.
이 경우는 좋지 않음으로 최적화하기 위해서 Trie와 Backtracking을 조합하고자 한다.
우선 Trie 구성은 2가지 방향에서 가능하다.
- Board의 글자를 Trie로 만든다
- Dictionary의 words를 Trie로 만든다.
Board의 글자를 Trie로 만들기 위해서는 최대 길이 m * n 의 word를 만들어야 해서 비효율 적이다.
Trie는 Node의 Depth가 늘어날 수록 search하는데 시간이 오래 걸린다.
그래서 Dictionary의 words를 Trie로 우선 만들어 보자
주어진 words는 ['oath','pea','eat','rain'] 이다

이런식으로 Trie가 생성된다. Child Node에서 분리되는 예제가 더 좋을 것 같지만 설명에서 나온 문제 임으로 그냥 쓴다.
이제 board를 아래와 같이 Backtracking 해 나간다.

(0,0)에서 지가하는 것이 하나의 dfs 주기라고 생각하자.
o에서 node가 있는가? o의 sub node 중에 'e' 또는 'a'로 시작하는 node가 있는가?
이런식으로
- node에 word가 존재하는 순간까지 내려가면 된다.
그러기 위해서 Trie의 자료 구조는 아래와 같이 만들었다.
function Node(character){
this.character = character;
this.next = new Map();
this.end = false;
this.word = null;
}
let Trie = (function () {
function Trie(){
this.root = new Node();
}
Trie.prototype.push = function (word) {
let node = this.root;
for (let i = 0; i < word.length; i++) {
if (!node.next.has(word.charAt(i))) {
node.next.set(word.charAt(i),new Node(word.charAt(i)));
}
node = node.next.get(word.charAt(i));
}
node.end = true;
node.word = word;
};
Trie.prototype.find = function (word) {
let node = this.root;
for (let i = 0; i < word.length && node != null; i++) {
node = node.next.get(word.charAt(i));
}
if(node !== undefined && node.end && node.word === word) return true;
else return false;
};
return Trie;
})();Node에 end와 word가 있는걸 확인하자.
이런식으로 더 깊게 내려가 보자.
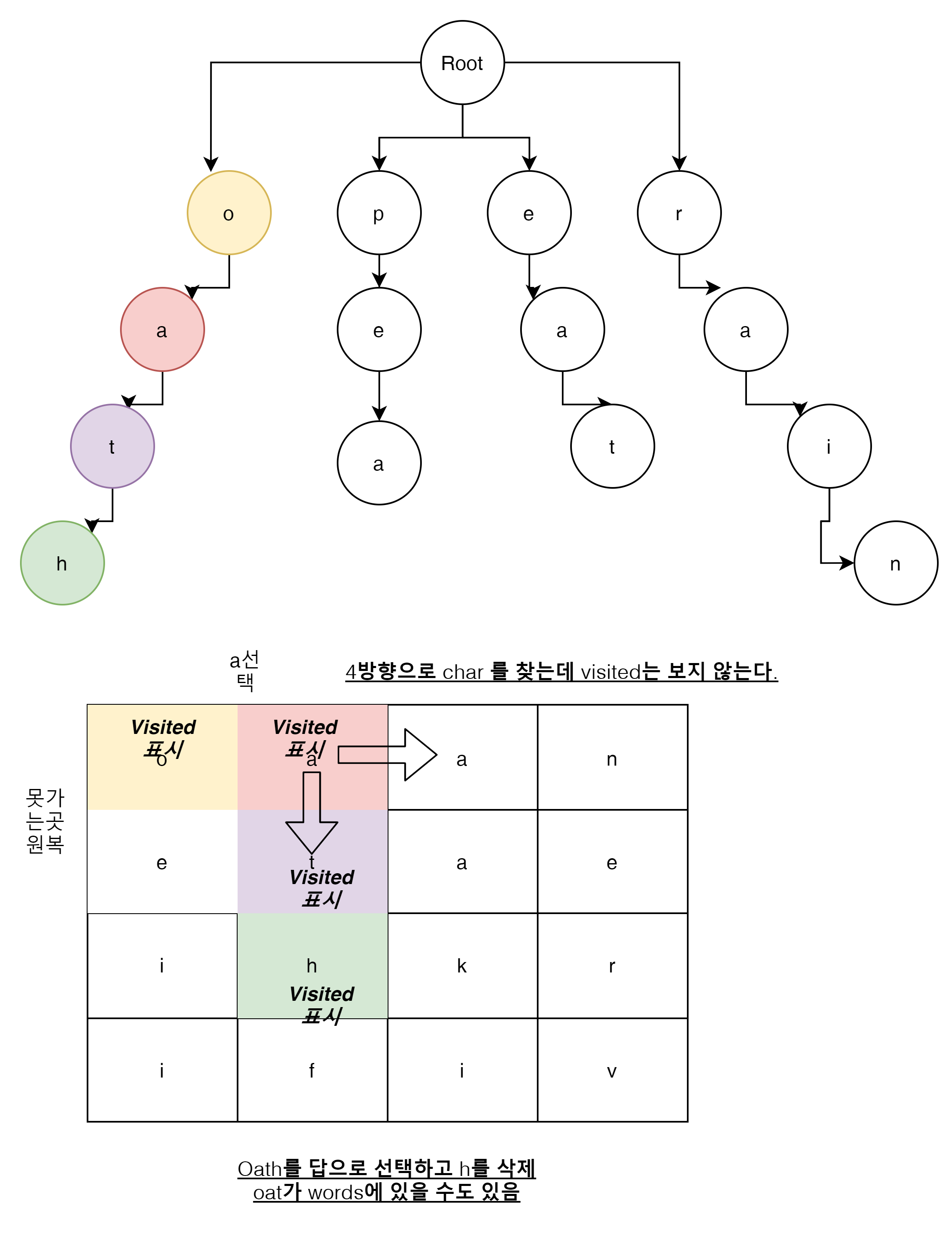
h Node에는 end가 true이고 word가 존재한다면 하나의 답이 된다.
같은 방식으로 h가 끝나고 t로 돌아 왔을 때 만약에 Dictionary에 'oat'가 있다고 하면 'oat'도 답이 된다.
이런식으로 계산 했을 때 최대 계산값은
$$ O(m * n^maxnodedepth) $$ 정도가 된다.
물론 여기서 빠진게 있다 바로 하나의 셀에서 주의의 셀로 dfs를 해나갈때 최대 3개의 cell로 분산이 될 수 있다는 것이다.
$$ O(m*n^{maxwordlength*3}) $$
이렇게 계산이 가능할 것으로 보인다.
그런데... 뭐 답은 $ O(M(4⋅3L−1)) $ 라고 하는데 잘 이해는 안된다. 혹시 아시는 분을 알려주세요~
var findWords = function(board, words) {
function Node(character){
this.character = character;
this.next = new Map();
this.end = false;
this.word = null;
}
let Trie = (function () {
function Trie(){
this.root = new Node();
}
Trie.prototype.push = function (word) {
let node = this.root;
for (let i = 0; i < word.length; i++) {
if (!node.next.has(word.charAt(i))) {
node.next.set(word.charAt(i),new Node(word.charAt(i)));
}
node = node.next.get(word.charAt(i));
}
node.end = true;
node.word = word;
};
Trie.prototype.find = function (word) {
let node = this.root;
for (let i = 0; i < word.length && node != null; i++) {
node = node.next.get(word.charAt(i));
}
if(node !== undefined && node.end && node.word === word) return true;
else return false;
};
return Trie;
})();
let trie = new Trie();
let result = new Array();
for (let i = 0; i < words.length; i++) {
trie.push(words[i]);
}
let tmpBoard = new Array(board.length).fill(0).map(_=> new Array(board[0].length).fill(false)); //visited check
for (let row = 0; row < board.length; row++) {
for (let col = 0; col < board[0].length; col++) {
backtracking(row, col, tmpBoard, trie.root);
}
}
function backtracking(row, col, visitedBoard, subTrie){
let rowDir = [-1, 0, 1, 0]; //up, right,down,left
let colDir = [ 0, 1, 0, -1];
if(subTrie.next.has(board[row][col])){
visitedBoard[row][col] = true;
let curTrie = subTrie.next.get(board[row][col]);
for(let i = 0; i < 4; i++){
let tmpRow = row + rowDir[i];
let tmpCol = col + colDir[i];
if (0 <= tmpRow && 0 <= tmpCol && tmpRow < visitedBoard.length && tmpCol < visitedBoard[0].length && !visitedBoard[tmpRow][tmpCol]) { //visited하지 않은 경우만 처리함
backtracking(tmpRow, tmpCol, visitedBoard, curTrie);
}
}
if (curTrie.end) {
result.push(curTrie.word);
curTrie.end = false;
}
visitedBoard[row][col] = false;
}
}
return result;
};
'Problem Solving' 카테고리의 다른 글
| Critical Connections in a Network (0) | 2021.06.11 |
|---|---|
| Sliding Window Maximum (0) | 2021.06.09 |
| Sudoku Solver (0) | 2021.05.23 |
| Minimum Window Substring (0) | 2021.05.22 |
| Binary Tree Maximum Path Sum (0) | 2021.05.21 |
