Critical Connections in a Network
문제 내용
노드와 nod-directed edges가 주어졌을 때, 어떤 edge가 없어지면 노드 그룹이 분리되게 되는 지 찾아라
접근 방법
이 문제는 하기 링크의 문제와 그 접근 방법이 같다.
2020.08.31 - [Problem Solving] - 1568. Minimum Number of Days to Disconnect Island
2가지의 문제 해결 방법이 있다.
- edge를 삭제하고 dfs를 순회한다.
- 타잔(tarjan) 알고리즘을 이용해서 critical edge를 찾는다.
우선 첫번째 방법을 알아보자
Edge를 삭제하고 dfs를 순회한다.
가장 접근 하기 쉬운 방법이다.
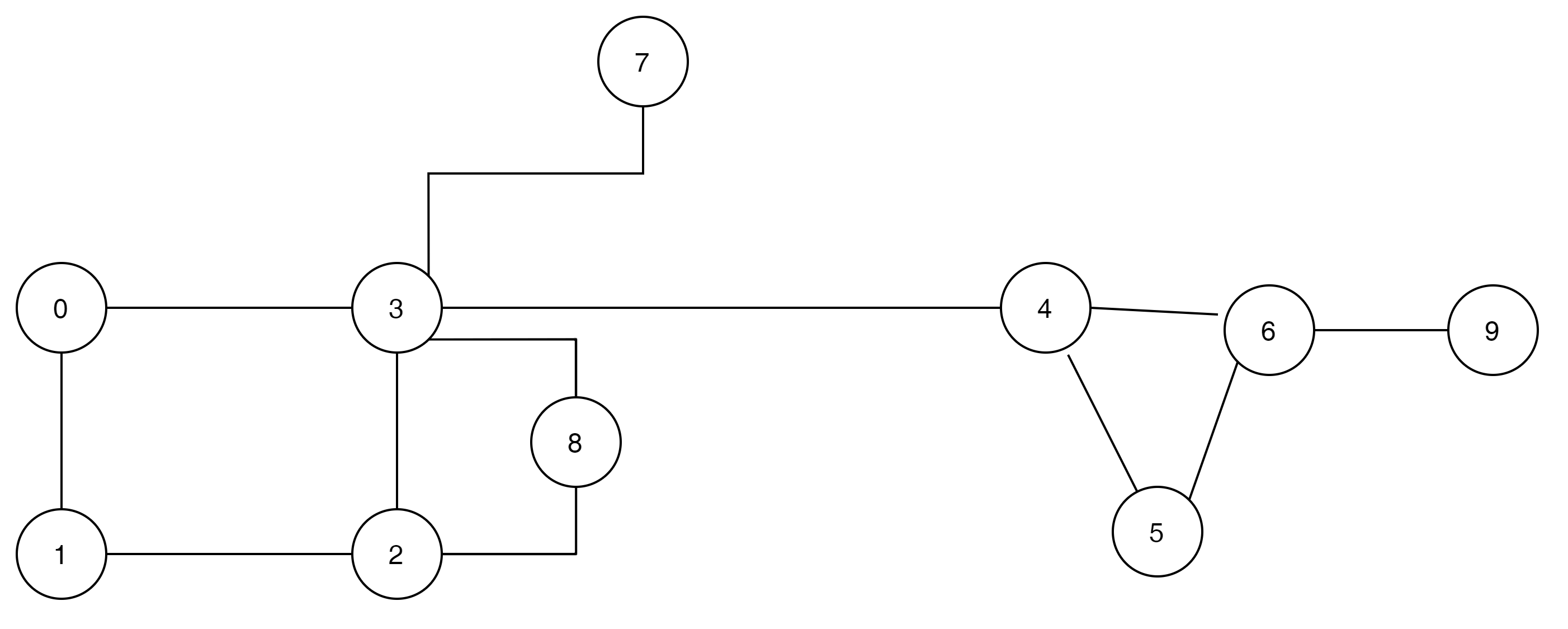
이렇게 생긴 문제가 주어졌다고 생각해 보자.
한눈에 보기에 답은

$ [3,7], [3,4], [6,9] $
가 답이된다.
이것을 알기위해 가장 쉬운 방법은 주어진 edge를 하나씩 자르고 dfs를 점검해 보는 것이다.

3과 7의 edge를 삭제한 후 0번 Node에서 DFS를 실행 시킬경우 7을 제외한 모든 노드를 순회할 수 있다.
즉, 이번에 삭제한 $ [3,7] $ edge가 답이 된다는 것이다.

만약에 $ [3,2] $ 가 삭제 되면 어떤가?
모든 Node를 순회할 수 있다.
즉, 이런식으로 모든 edge를 끊어가면서 순회를 하게 되면 정답을 찾을 수 있다.
이 경우의 Time complexity는
모든 노드 갯수 Vertex * 순회가능한 Edge의 수가 됨으로
$$ O(VE) $$
가 된다.
그럼 이보다 더 빠른 방법은 없을까?
Tarjan(타잔) 알고리즘을 사용하자.
타잔 알고리즘을 사용하기 위해서는 다음과 같은 전제 사항을 이해해야 한다.

상기와 같이 3개의 노드가 있다고 생각해 보자.
1번은 2번노드를 갈수 있고 2번 노드는 3번 노드를 갈수 있다. 3번 노드는 최종적으로 1번 노드를 접근할 수 있다.
이렇게 모든 노드가 서로 연결되는 것을 Strongly Connected Component(SCC)라고 한다.
그럼 여기에 노드를 하나더 붙여 보겠다.
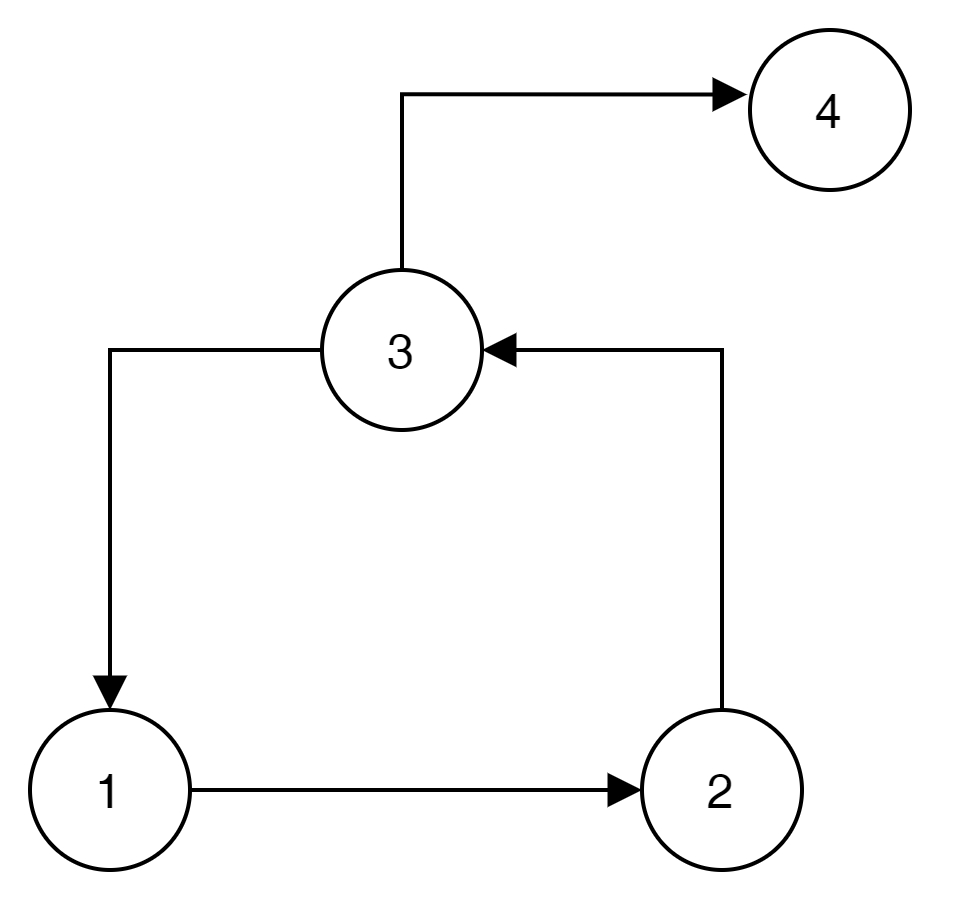
이 경우는 4번 노드가 3번 노드로 다시 돌아 갈수 없음으로 4번 노드는 SCC의 대상이 되지 않는다.
그렇다면, 상호 참조를 하게 되면 어떨까?

이 경우는 4번이 3번으로 와서 다시 1번으로 갈수 있는 길이 있음으로 SCC라고 불러도 된다.
그러나 모든 Edge에 방향성이 없다면 어떻게 될까?

3번과 4번을 연결하고 있는 2개의 edge는 하나로 생각해도 문제가 없게 된다.

이렇게 변경이 되는데 이렇게 된다면, 타잔알고리즘의 규칙으로는 [1,2,3,4]번 노드 모두 SCC의 Group 대상으로 본다.
우리가 찾아야 하는 것은 3번과 4번 라인이다. 이 부분이 SCC를 Grouping하는 방식과 다른 부분이라고 생각하면 된다.
이제 1번 Node부터 타잔 알고리즘으로 DFS를 Counting 해보도록 하겠다.
시작된 Node를 1이라고 생각하고 하나의 Edge를 지나갈때 마다 Count를 1씩 증가하는 방식이다.
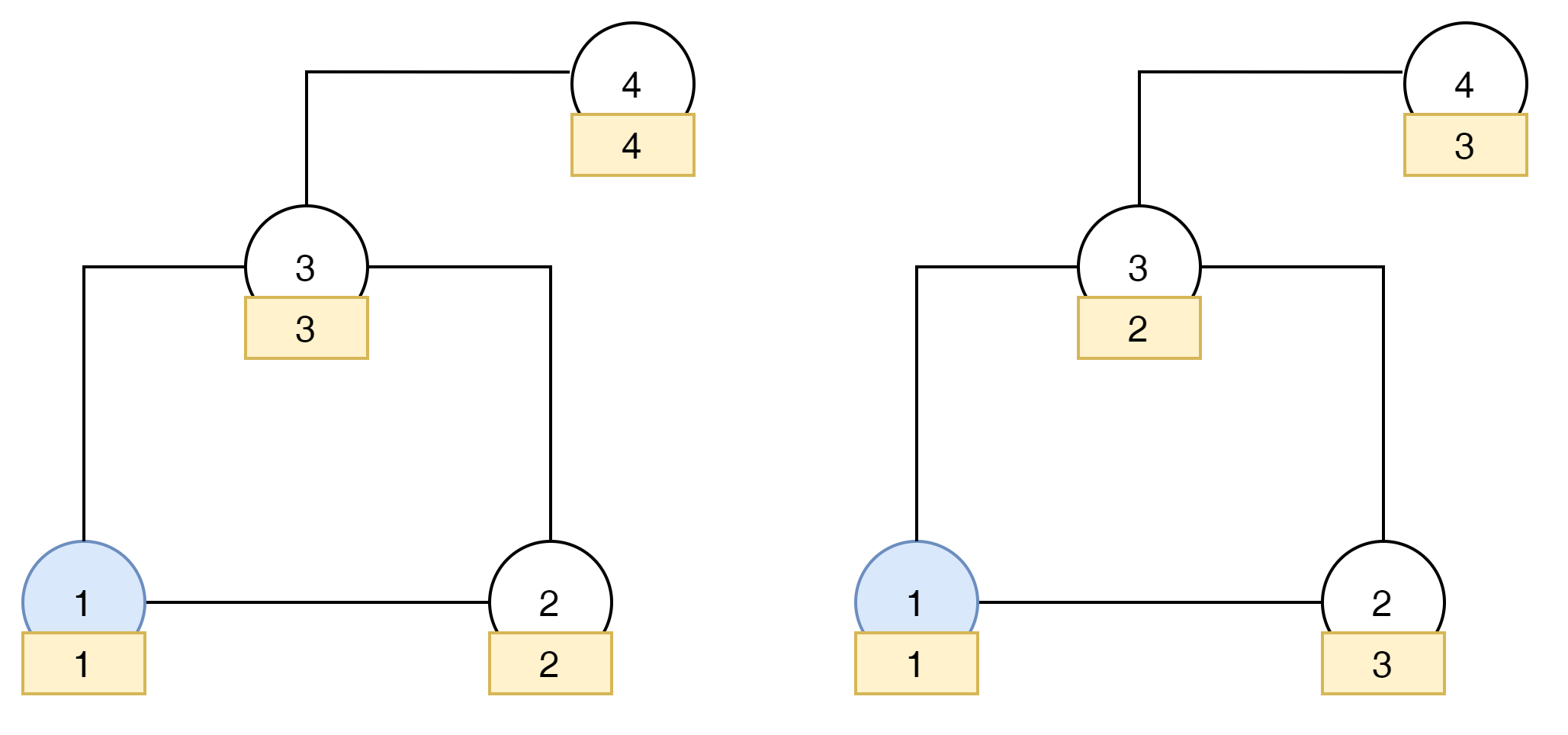
1번 노드에서 부터 시작된 카운트는 위의 2가지 경우로 나타낼 수 있다.
이 Counting을 할 때 다음과 같은 규칙을 갖는다.
- 나를 부른 Node를 Next Node로 갖지 않는다. (DFS 임으로)
- 나를 부르지 않고 내가 갈수 있는 Node에 이미 Count가 있다면 해당 Count가 내 Count보다 낮은 경우 적용
- 내 Count와 내가 부른 다음 Node의 Count가 같다면 DFS는 종료 되었고, 해당 DFS시 지나간 모든 Node는 SCC Group이다.
- 단, 내가 부른 다음 Node가 어떤 사유에서인지 내 Node의 Counter보다 높다면 Critical Edge이다.
이 규칙을 바탕으로 최종적 Label을 붙여 보겠다.

3번 노드는 1번 노드와 4번 노드로부터 Count를 받을 수 있다.
1번은 1, 4번은 4번 Count이다. 이 중에 가장 낮은 Count를 선택한다. 즉 1을 선택한다.
이때 4번 Node는 3번 Node보다 더 큰 count를 return한다. Critical Edge로 처리하자.
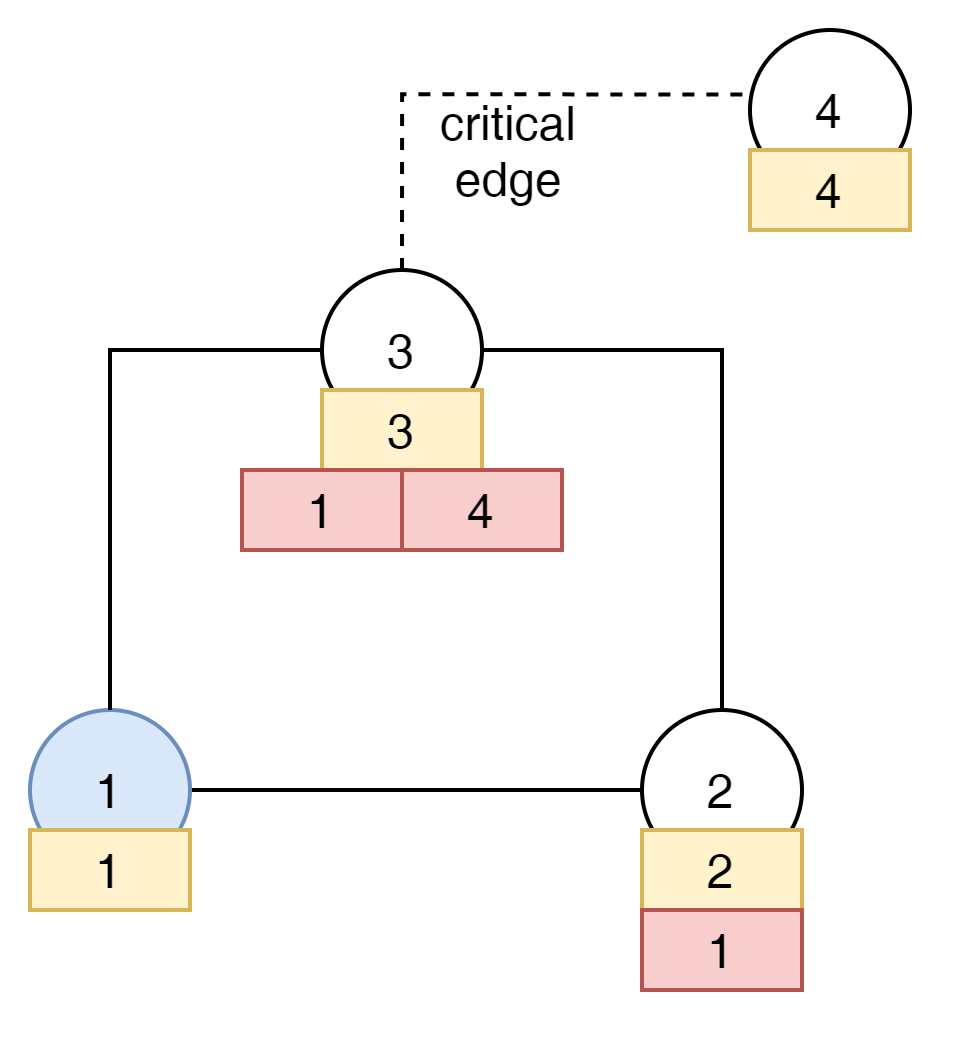
3번 노드는 가장 작은 Count인 1을 2번 노드로 보낸다.
다시 2번 노드는 1번 노드에게 가장 낮은 1번 노드를 돌려 보낸다.

1번 노드는 자신과 동일한 count가 회기 했기 때문에 이른 지나간 모든 Node를 SCC Group으로 생각하고 DFS를 종료한다.
상기 Case의 경우 답은 $ [3,4] $ 가 되게 된다.
다음으로는 2번 노드에서 4번 노드까지 DFS를 진행 하면 되지만 이미 Count가 정해진 상태이고 SCC로 묶였기 때문에 더이상 진행할 필요 없다.
즉 한번 Count가 Label로 고정된 Node들은 모두 Node Cut, 삭제 되어도 상관이 없는 상태가 된다.
앞서 예를 들은 문제 같은 경우는 아래 그림처럼 Count를 순회하게 된다.
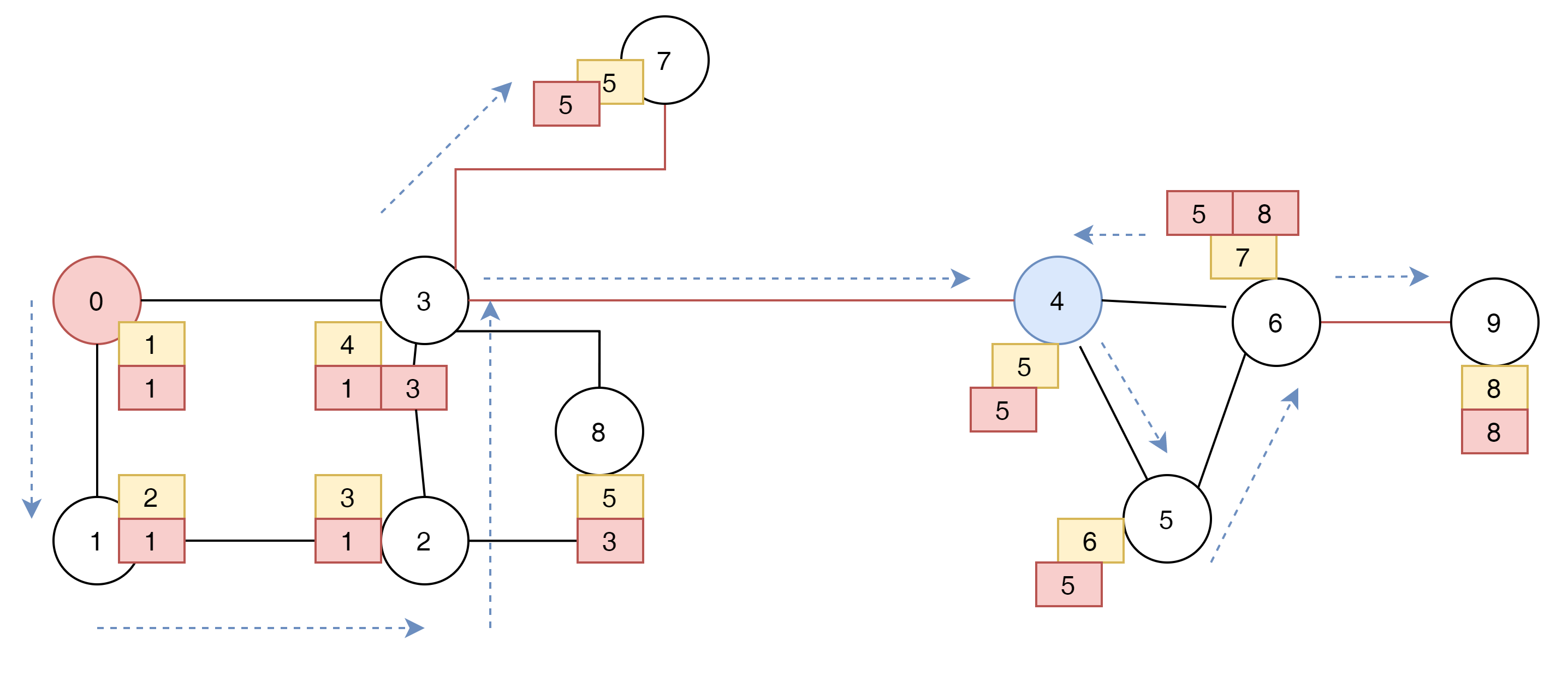
여기서 확인해야 할 것은 3번 노드와 7번 노드의 Count를 보면 7번 노드는 3번 노드 Count 보다 높은 값은 반환한다. 4번 노드는 3번 노드보다 높은 값을 반환한다. 9번 노드는 6번 노드보다 큰 값을 반환 함으로써 답은 $ [3,7],[3,4],[6,9] $ 가 되게 된다.
Time complexity는 한번 Node가 Edge를 타고 순환하고 나면 DP로 Label을 저장하게 되고, 한번 저장된 Node는 해당 Label을 재활용 하게 됨으로
$$ O(V + E) $$
가 되게 된다.
class Node {
constructor(){
this.next = new Array();
this.count;
}
}
var criticalConnections = function(n, connections) {
let nodes = new Array(n).fill(0).map(_=> new Node());
let dp = new Array(n).fill(-1);
let result = new Array();
for (let [start, end] of connections) {
nodes[start].next.push(end);
nodes[end].next.push(start);
}
// console.log(nodes);
for (let i = 0; i < n; i++) {
journey(-1, i, 1);
}
// console.log(dp);
return result;
function journey(start, end, count){
if (0 < dp[end]) return dp[end];
dp[end] = count;
let min = Number.MAX_SAFE_INTEGER;
for (let next of nodes[end].next) {
if(next != start){
let jourVal = journey(end, next, count + 1);
min = Math.min(min, jourVal);
if (count < jourVal) {
result.push([end, next]);
}
}
}
dp[end] = Math.min(count, min);
return dp[end];
}
};
// console.log(criticalConnections(5, [[0,1],[1,2],[2,0],[1,3],[3,4],[4,0]]));
'Problem Solving' 카테고리의 다른 글
| Remove Invalid Parentheses (0) | 2021.06.14 |
|---|---|
| Regular Expression Matching (0) | 2021.06.13 |
| Sliding Window Maximum (0) | 2021.06.09 |
| Word Search II (0) | 2021.05.25 |
| Sudoku Solver (0) | 2021.05.23 |
