문제 내용
1차원의 숫자 배열 Array가 주어졌을 때
일정한 범위의 widow size 만큼의 길이 안에서 최대 Number 값을 찾아라
접근 방법
2가지로 접근이 가능한다.
- Doubled Array List
- Dynamic Programming
Doubled Array List로 접근을 알아보겠다.
Doubled Array List는 java 경우 Deque이용해서 Head와 Tail을 O(1)의 시간으로 접근 가능하고 Head, Tail 삭제도 O(1)로 가능하다.
단, removeFirstOccurence 같은 경우는 값을 찾아야 해서 O(N)의 시간이 걸린다.
Deque를 사용하는 경우 javascript는 직접 구현을 해줘야 하는게 있어서 간단히 그림으로 아래 설명만 하고자 한다.

문제가 위와 같이 주어졌다고 하면,
Deque를 이용해서 항상 Head에는 가장 큰 값을 유지 하도록 한다.
최초값 1을 넣는다.

다음으로 3을 넣는다.

Head에 가장 큰값을 유지 한다고 했음으로 1의 값은 삭제되어야 한다.

다음으로 -1을 Queue에 넣게 되면

k사이즈인 3을 만족하게 된다. Head에 가장 큰값을 유지 함으로 이때 result는 3을 추가하게 된다.

다시 -3을 추가한다.

-3의 index가 3이고 Head의 첫번째 인댁스가 1임으로 size k를 만족하고 2번째 결과값도 3이된다.
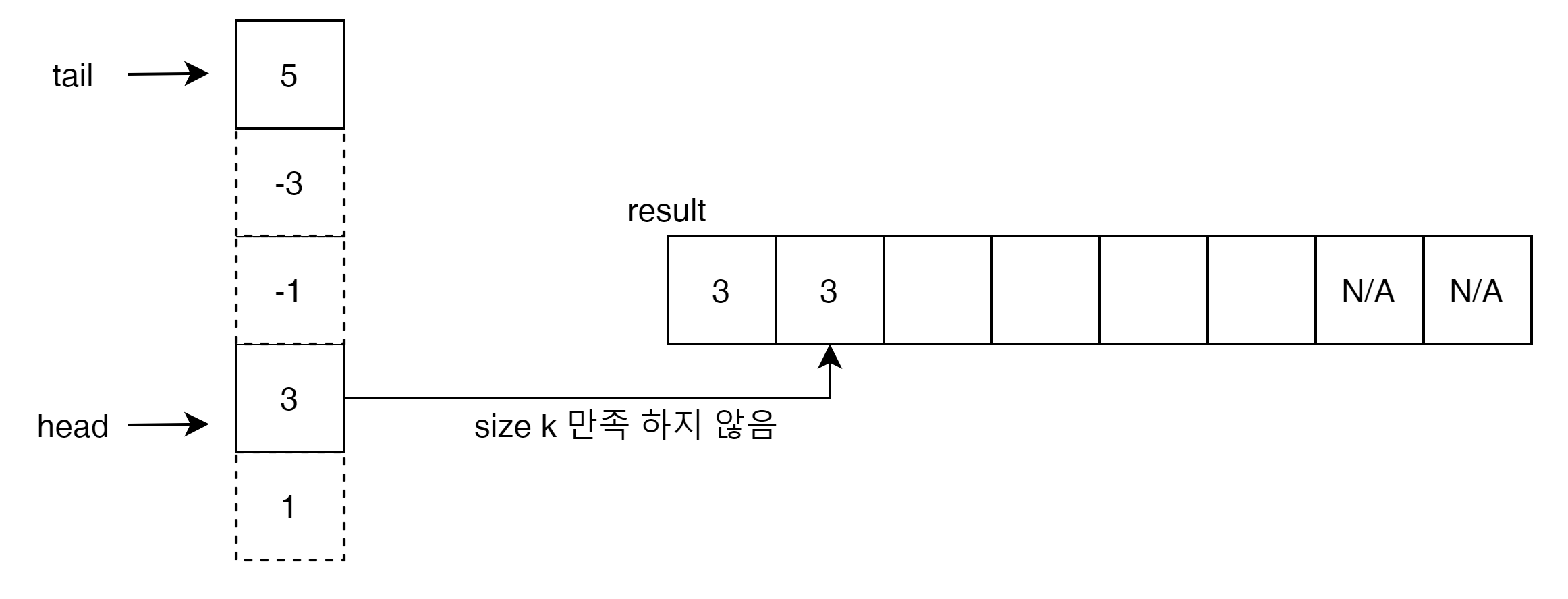
5가 들어오면 가장 큰값이 5가 됨으로 -3과 -1을 삭제 되게 된다. 현재 Head에 위치한 3의 index는 1로써 size의 범위를 벗어나게 된다. 물론 5보다도 작기 때문에 문제가 없겠지만, Size의 범위를 벗어난 값은 삭제 되어야 한다.

이런식으로 진행을 하면

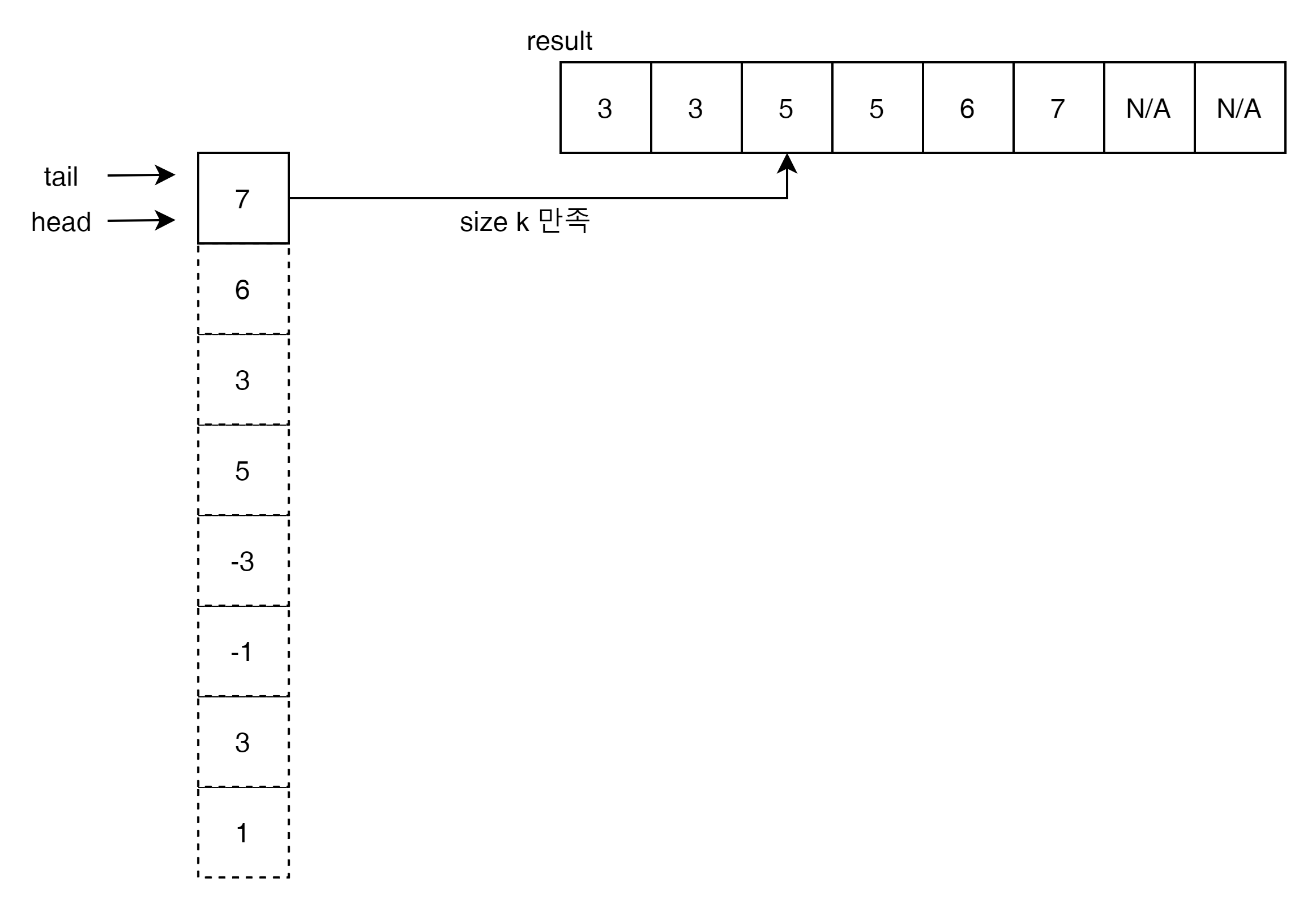
이렇게 진행을 하게 된다. Time Complexity는 O(N)으로 충분하다.
두번째로 Dynamic Programming을 살펴 보겠다.
기본적인 아이디어는 k라는 넓이를 이용한 Segmentation이라고 보는게 좋을 것 같다.
아래와 같이 문제가 주어졌을 경우 k의 size 만큼 Segmentation을 해주겠다.

아래 그림과 같은 형태가 된다.

가장 쉬운 형태로
1에서 -1까지의 가장 큰값은 3이된다.
-3에서 5사이의 가장 큰값으 5이다.
6에서 7은 7이다.
그렇다면 중간값은 어떻게 해야할까?
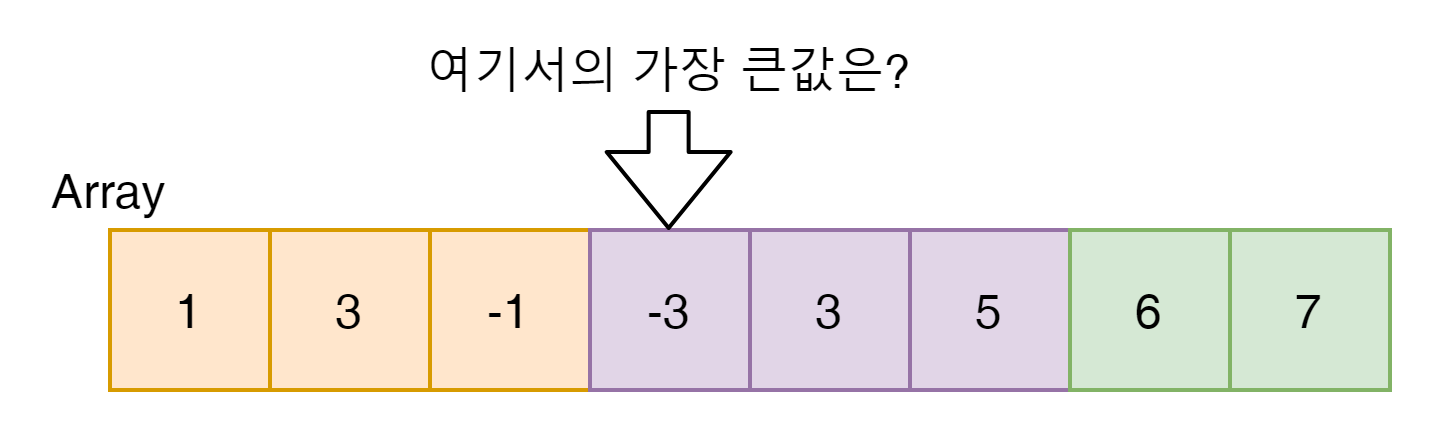
-1까지의 가장 큰 값은 3이라는 것을 알았는데 -3을 마지막 index로 하는 가장 큰값은 무었일까?
[3,-1,-3]에서 가장 큰값인 3이 될 것이다.
하지만 매번 Range 검색을 하는 것은 좋지 않다.
여기서 아이디어를 낼수 있는 것은
왼쪽 블럭범위에서 가장 큰값과 오른쪽 블럭에서 가장 큰 값을 찾으면 된다는 것이다.

3이라는 사이즈를 조금더 보기좋게 4라는 크기로 키워 보도록 하겠다.

이렇게 보면 주황색 n3, n2에서 가장 큰값과 보라색 n0와 n1사이의 가장 큰값을 찾으면 된다.
즉, 주황색 n3, n2 right에서 left로 누적된 max값을 저장하고
보라색 n0와 n1 left에서 right로 누적된 max값을 저장하면 된다.
원래 문제로 돌아가서 생각해 본다면
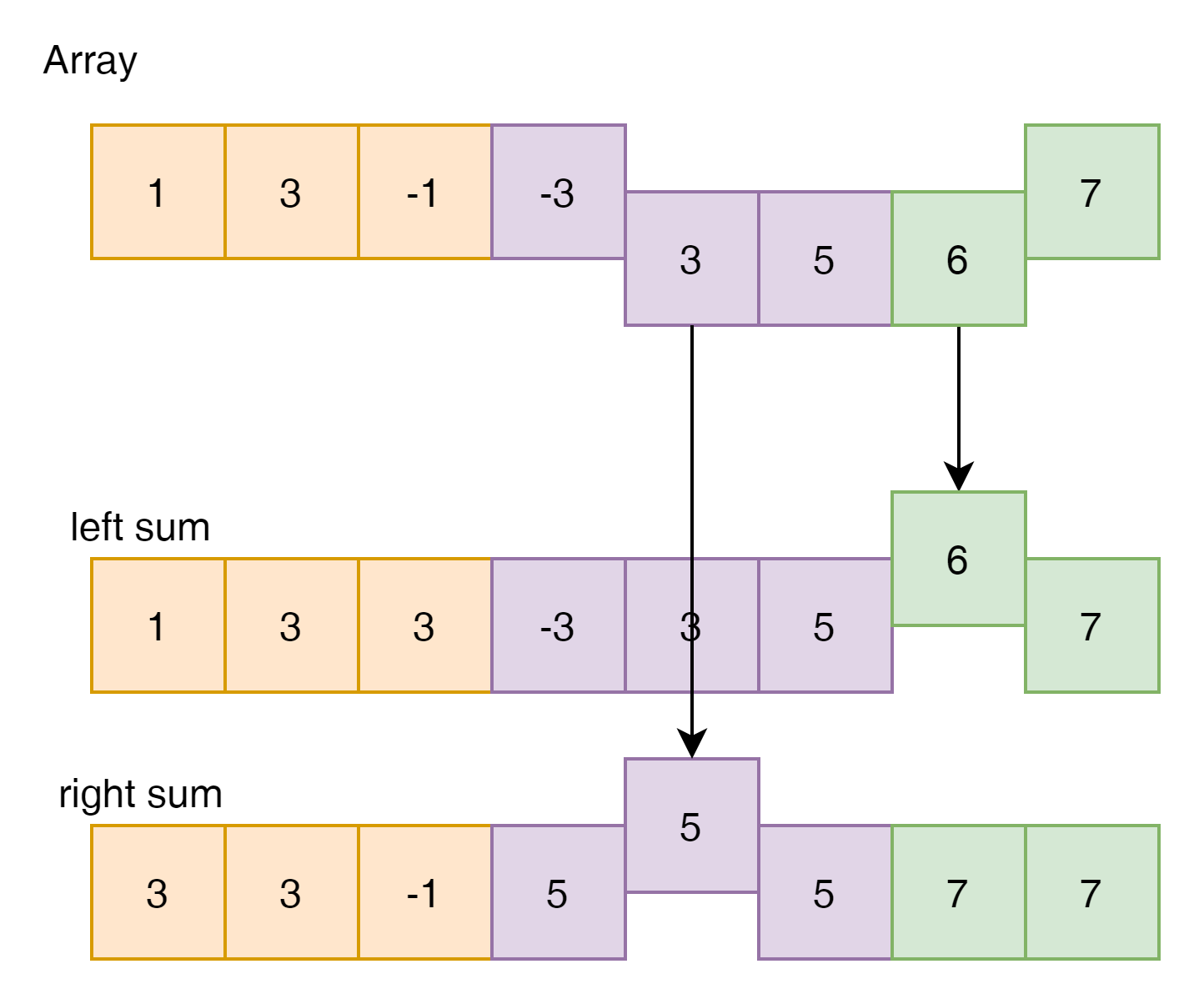
이렇게 오른쪽 블럭은 left sum에서 최고 값을
왼쪽 블럭은 right sum에서 최고 값을 찾아서
$$ Max(leftsum(size_0), rightsum(size_{k-1})) $$
을 처리하면 된다.
$$ O(N) $$
Time Complexity역시 Double Linked List와 같다.
var maxSlidingWindow = function(nums, k) {
let left2rightSum = new Array(nums.length);
let right2leftSum = new Array(nums.length);
let result = new Array(nums.length - k + 1);
let max = nums[0];
for (let i = 0; i < nums.length; i++) {
if (i % k === 0) max = nums[i];
if(max < nums[i]) max = nums[i];
left2rightSum[i] = max;
}
max = nums[nums.length-1];
for (let i = nums.length - 1; 0 <= i ; i--) {
if (i % k === k - 1) max = nums[i];
if(max < nums[i]) max = nums[i];
right2leftSum[i] = max;
}
for (let left = 0; left < nums.length - k + 1; left++) {
let right = left + k - 1;
result[left] = Math.max(right2leftSum[left], left2rightSum[right]);
}
return result;
};'Problem Solving' 카테고리의 다른 글
| Regular Expression Matching (0) | 2021.06.13 |
|---|---|
| Critical Connections in a Network (0) | 2021.06.11 |
| Word Search II (0) | 2021.05.25 |
| Sudoku Solver (0) | 2021.05.23 |
| Minimum Window Substring (0) | 2021.05.22 |
