문제 내용
s와 p라는 문자열이 주어진다.
p는 일반 영문자와 아래 2개의 char로 구성될 수 있다.
- `.` : 단 한개의 모든 char 종류와 동일하다
- `*` : * 직전에 오는 char가 0개 이상 존재 할 수 있다.
s와 p가 동일한 문자열이 가능한지 비교하라
접근 방법
가장 쉬운 방법 부터 생각을 해보자
`*` wildcard가 없는 경우를 생각하자.
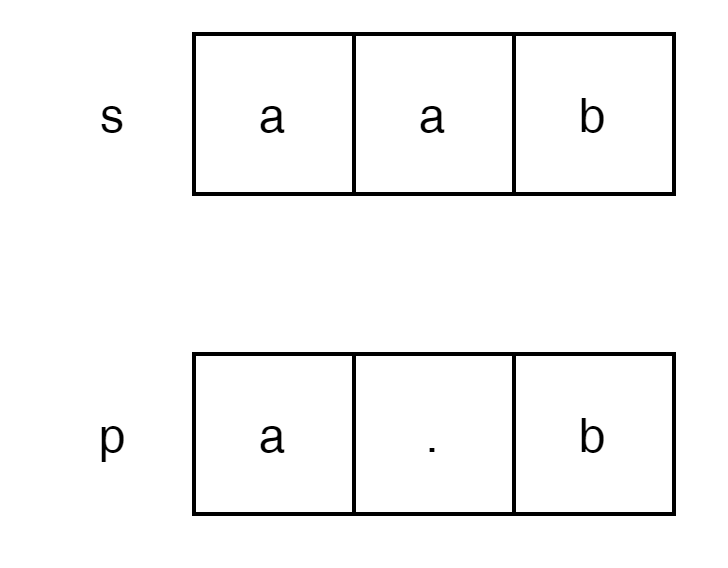
단순히 왼쪽에서 오른쪽으로 s와 p의 index를 하나씩 움직여 가면서 모든 문자열이 동일한지 확인 하고
만약에 동일하지 않은 것이 나오면 false를 return 하면된다.
주의 해야할 것은 `.`이 모든 문자열을 대치 할 수 있다는 것이다.
그러면 wildcard가 들어간다고 생각해 보자.

이 경우는 p가 다음과 같은 경우의 수로 만들어 질 수 있다.

즉 wildcard는 0개 이상의 char가 존재 가능한데 이중에서 가장 적절한 값을 matching 시키면 된다.

상기 그림에서는 a가 2개인 경우 답이 된다.
이와 같은 패턴을 이용해서 다음과 같이 Dynamic Programming 형태로 생각을 해보는 것이 가능하다.
Dynamic Programming

wildcard가 있는 a가 나올 수 있는 최대 횟수는 s의 길이를 넘지 못한다.
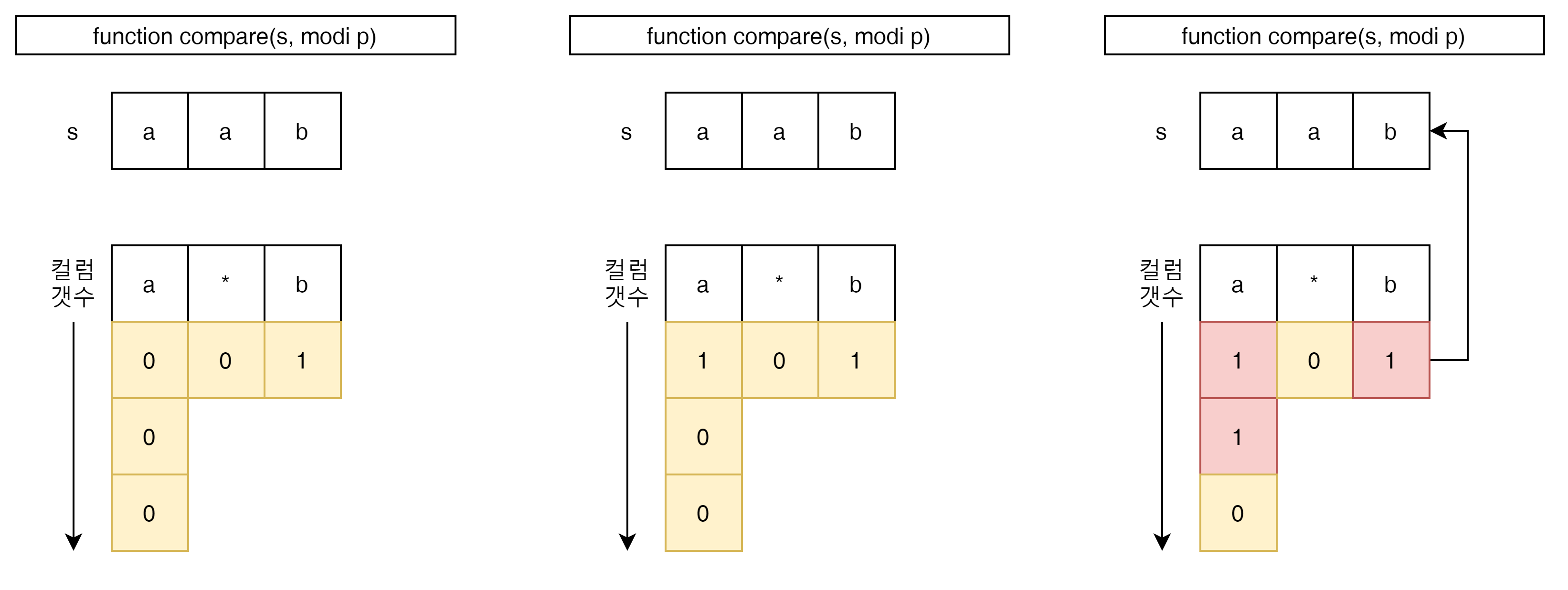
이 경우는 3번째 a가 2번 들어간 경우 compare가 성공하게 된다.
이런식으로 wildcard의 컬럼 갯수를 늘려가면서 특정 범위의 s와 pattern이 match하는지 확인해 볼 수 있다.
결과적으로 상위 그림으로 보자면
s의 길이가 0에서 2이고 dp가 0에서 2인 pattern match는 true라고 생각할 수 있다.
이것을 dynamic programming으로 저장을 해볼수 있다.

상기와 같은 식이다.
그럼 다시 상기 그림을 바탕으로 Top Down 으로 접근해보자.

a가 0회 사용되었다고 생각하고 p의 point를 b로 이동시키고 s와 비교해 보자.
비교결과가 다름으로 dp(0,2)는 false가 된다.
그럼 a를 한번 증가 시켜 보자.

여기서 1회 증가 시킬 수 있는 전제 사항은 s의 index값과 p의 index값이 서로 같다는 전제가 된다.
상기 와 같은 상태에서는 다시 한번더 a를 0회 또는 1회를 더 할지 선택을 할 수 있는 상태가 된다.
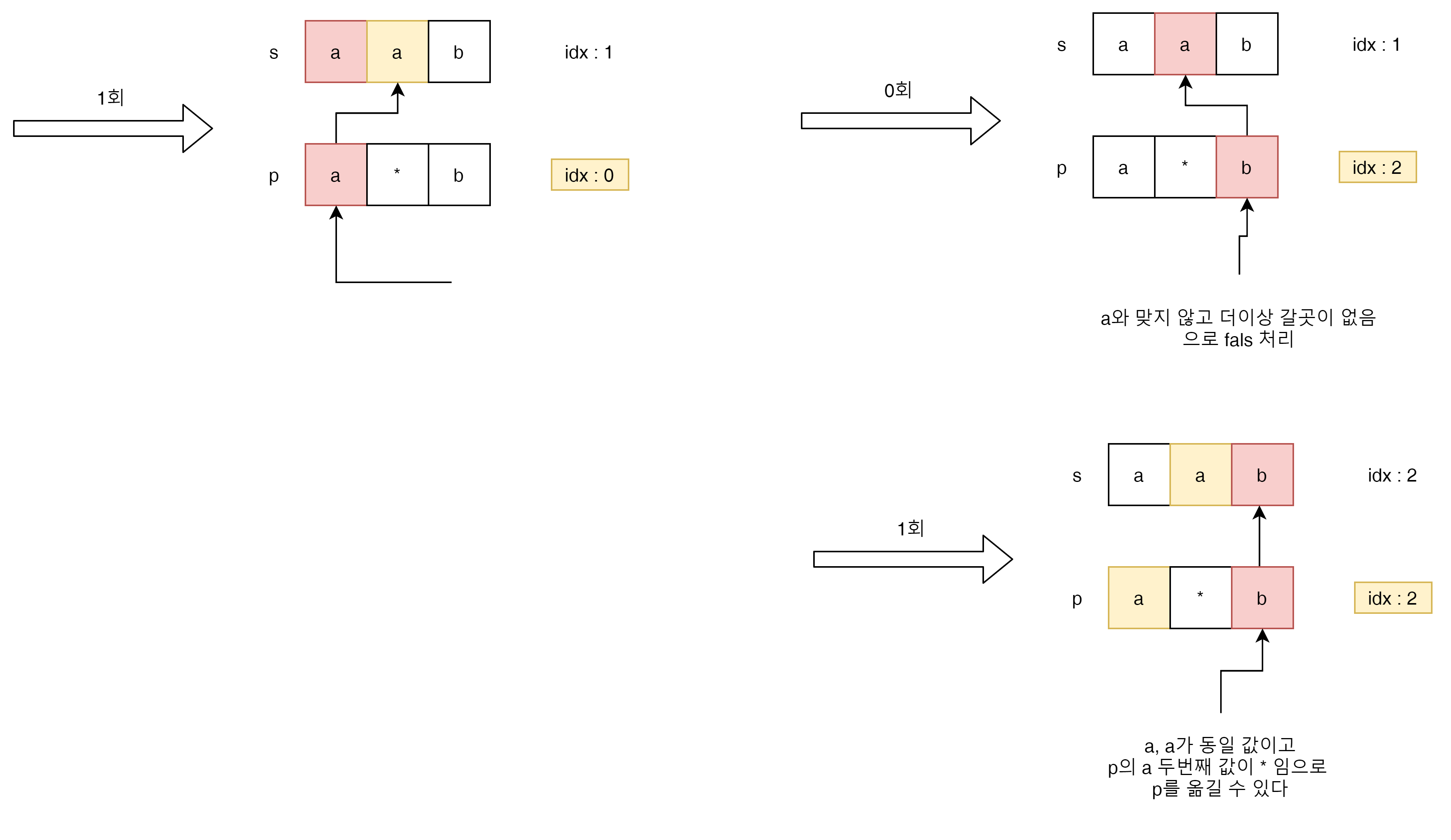
1회 a를 사용한 상태에서 다시 한번더 a를 활용 할 수 있거나 혹은 포기 할 수 있다.

한번더 활용하지 않는다면 s의 index는 1을 가르키고 p는 2를 가르킨다 두개의 값을 비교해보면 다름을 알 수 있다.

false가 되게 된다.

그럼 a를 한번더 활용해보자 index 1과 p index 1간에 'a'가 동일 값임으로 1회더 사용하고 index를 오른쪽으로 옮길수 있다.
그럼 상기 그림과 같이 'b'가 양쪽다 동일하게 되고 true가 된다.

그럼 dp(2,2)는 true가 되게 되고 backtracking을 하면서 dp(2,2)를 호출한 index는 true로 변경된다.

최종적으로 dp(0,0)이 true가 됨으로 해당 문제는 true가 되게 된다.
Time Complexity는 2D DP size를 채우는 만큼 일어 남으로 최대
$$ O(s length * p length) $$
가 된다.
이 방법 말고 한가지 방법이 더 있다.
Stack & Backtracking 을 사용하는 방법
가장 중요한 이 문제의 핵심은
- wildcard는 0번 이상이 나올 수 있다.
라는 것이다.
이를 이용해서 stack을 활용하는 것을 접근 하려고 하는데 그전에 다음과 같이 문제를 수정할 필요가 있다.
- `*` :
* 직전에 오는 char가 0개 이상 존재 할 수 있다. - `*` : * 직후에 오는 char가 0개 이상 존재 할 수 있다.
문제를 왼쪽에서 오른쪽으로 선형적으로 compare하기위해서 문제를 변경하였다. 그렇게 하지 않으면 위에 Dynamic Programming처럼 wildcard가 뒤에 있는 지를 확인하는 것이 불편한 부분이 있어서이다.

이렇게 문제를 변경하고 좌측에서 우측으로 position을 옮겨 가보자.
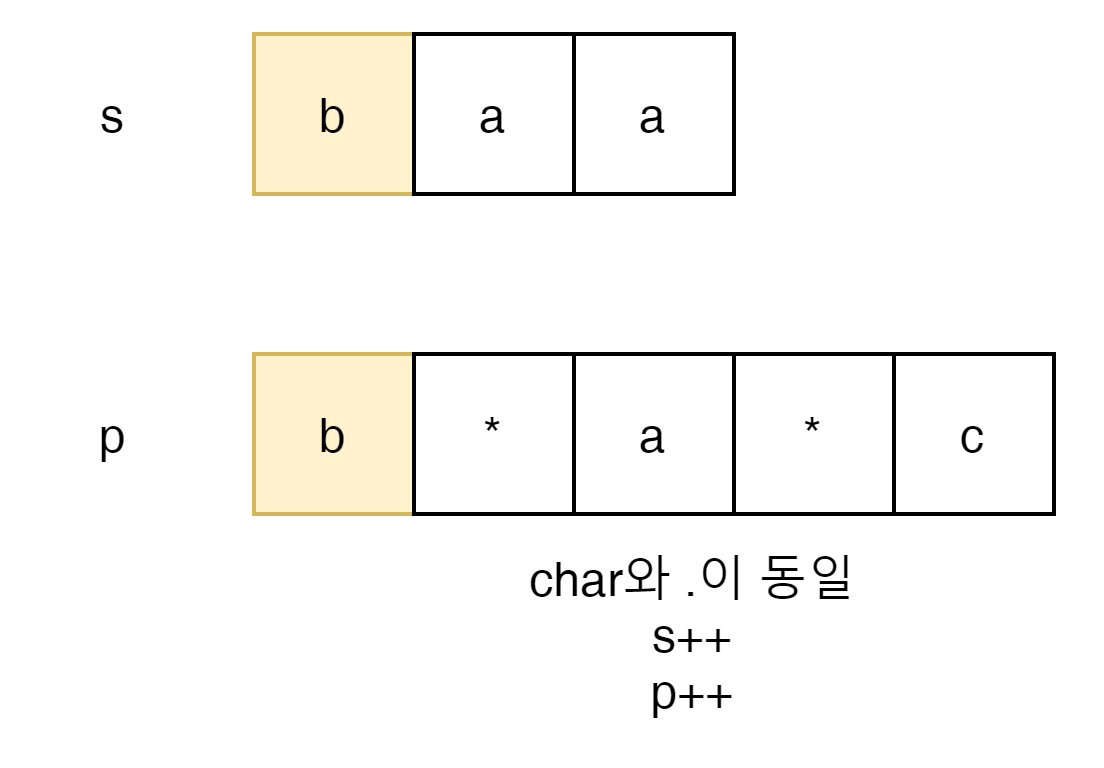
index의 값이 동일 하거나 `.` 일 경우 오른쪽으로 index를 이동 하면 된다.

p의 경우 `*`가 나오게 되면 이 wildcard의 상태를 저장해 놓아야 한다.
왜냐하면 이 부분부터 0개 이상의 a가 나올 수 있기 때문이다.
이때 저장해 놓아야 할 상태는 (s의 position, p의 position)이다.
첫번째는 무조건 0번 사용한다고 생각하고 상태를 넣어 놔야 한다.

0번 사용한다고 생각하고 p를 우측으로 옮겨 보자. 그런데 다시 한번더 wildcard가 나왔다.
여기서 wildcard 상태를 다시 저장하게 되면 앞서 저장해 놓은 `*a`의 상태가 사라지게 된다.
그래서 상태저장을 위해서 stack을 사용하였다.

즉 *a와 *c의 상태를 stack에 넣어놓고 필요에 따라서 사용하고자 하였다.

다시 돌아가서 *c 가 0회 사용된다고 생각하면, 더 이상 p index가 갈 곳이 없게 된다. 그럼으로 해당 비교는 false가 되게 되는데 wildcard stack에 남아 있는 값들이 있음으로 이를 최 상위부터 다시 활용 할 수 있다.
최상위 값인 s Position과 p Position을 다시 갖어와서 비교하자. 대신 현재 상태가 wildcard 상태라는 것을 꼭 저장해 놓자.
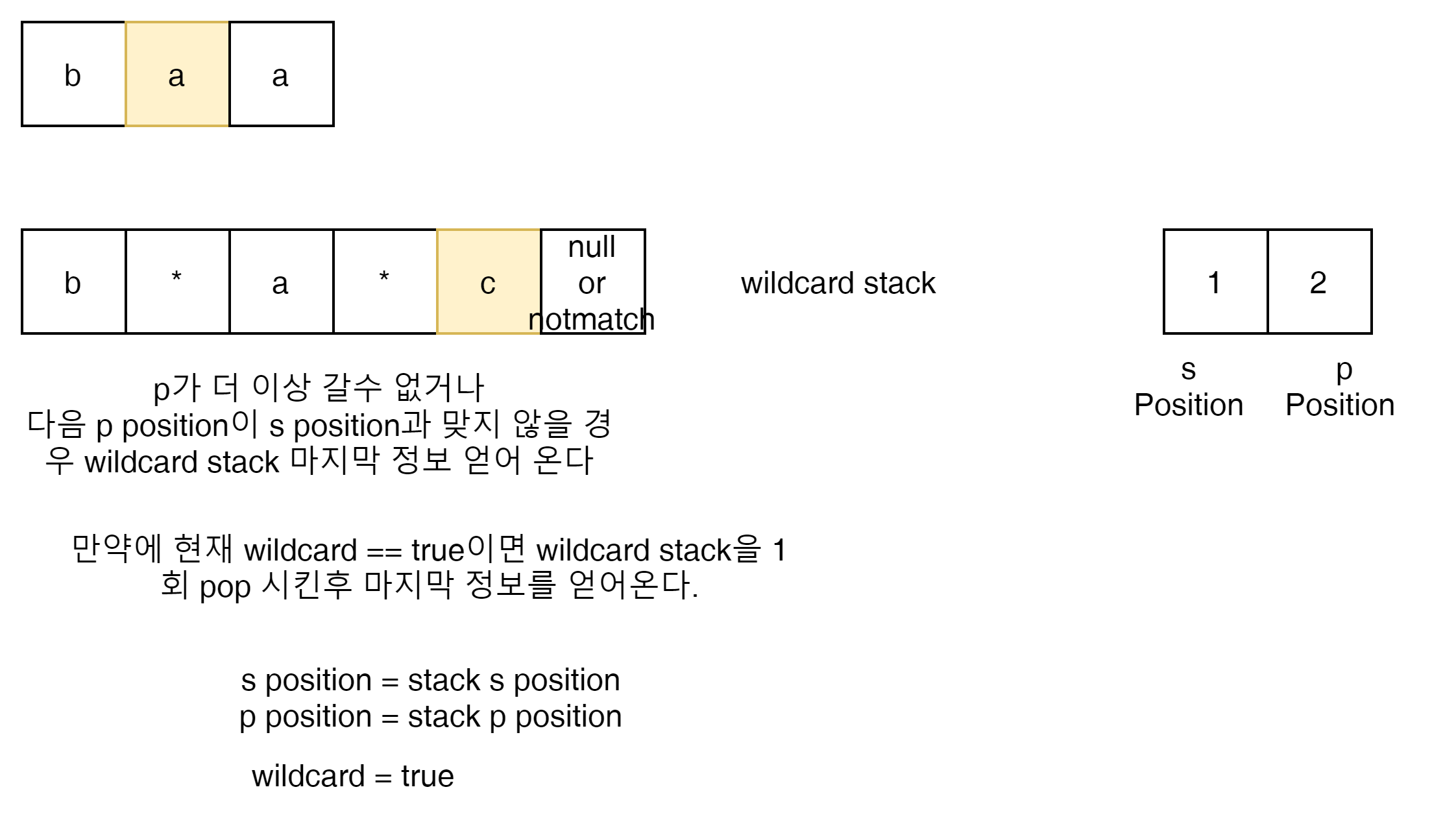
마지막 상태였던 'a'와 'c'를 비교했을 때 서로 같지 않음을 알 수있다. wildcard 상태에서 비교했을 때 같지 않음으로 해당 wildcard는 더이상 불필요 하다. 마지막 stack을 pop 처리 하자.
만약 stack에 더이상 값이 없다면 false를 return 할 수 있지만, 아직 한개의 wildcard가 남아있다.
상태를 다시 load 하자.

다행히 *a와 a가 동일하다. s의 포지션과 p의 포지션을 옮길 수 있게 되었다.
이때 주의해야 할 것은 wildcard의 상태 status를 꼭 업데이트 해줘야 한다.
기존 1이 었던 s Position을 2로 변경한 것을 확인 가능하다.
즉, 기존에 wildcard는 0회라고 생각하고 compare를 진행 했다면 이번에는 wildcard a가 1회 사용이 되고 오른쪽으로 옮겨졌다고 생각할 수 있게 된다.

다시 c의 wildcard가 나왔다. 상태 status를 stack에 넣어 준다.

더이상 갈곳이 없고 'a'와 'c'가 같지 않음으로 다시 stack을 pop한다.

다시 상태를 load하고 `a'와 `a`를 다시 비교하였다.
성공적으로 s의 값을 순회 하였다.
아직 남은것은 p의 문자열이 남았는데,
- 남은 문자열은 무조건 wildcard로만 구성이 되어있어야 한다.
그외의 값이 나머지 문자열에 있다고 하면 false를 return 해야 한다.
time complexity는 $$ O(s length * log P length) $$ 이다
이것은 증명이 필요한 문제로
https://arxiv.org/pdf/1407.0950.pdf
증명은 이곳에서 확인 가능하다.
var isMatch = function(s, p) {
s = s.split('').reverse().join('');
p = p.split('').reverse().join('');
let wildcardStack = new Array(); //[sIdx, pIdx]
let sIdx = 0;
let pIdx = 0;
let isWildcard = false;
while (sIdx < s.length) {
if (s.charAt(sIdx) === p.charAt(pIdx) || p.charAt(pIdx) === '.') {
sIdx++;
pIdx++;
if(isWildcard){
let [wsIdx, wpIdx] = wildcardStack[wildcardStack.length - 1];
wildcardStack[wildcardStack.length - 1] = [sIdx, wpIdx];
isWildcard = false;
}
} else {
if(p.charAt(pIdx) === "*"){
wildcardStack.push([sIdx, ++pIdx]);
pIdx++;
} else {
if(isWildcard){ //wildcard인데 맞지 않은 거면 stack pop
wildcardStack.pop();
isWildcard = false;
}
if (0 < wildcardStack.length) { //wildcard에 아직 남아 있는게 있다면
[sIdx, pIdx] = wildcardStack[wildcardStack.length-1];
isWildcard = true;
} else {
return false;
}
}
}
}
// console.log(wildcardStack);
if (pIdx < p.length) {
while(p[pIdx] === '*' && pIdx < p.length) pIdx += 2;
if (pIdx < p.length) return false;
}
return true;
};'Problem Solving' 카테고리의 다른 글
| Binary Search Lower Bound와 Upper Bound (0) | 2021.06.17 |
|---|---|
| Remove Invalid Parentheses (0) | 2021.06.14 |
| Critical Connections in a Network (0) | 2021.06.11 |
| Sliding Window Maximum (0) | 2021.06.09 |
| Word Search II (0) | 2021.05.25 |
