이진검색은 많은 곳에서 사용되는데 의외로 Lower Bound와 Upper Bound 문제가 나오면 정확한 코드를 만들지 못해서 쉬운 풀이임에도 틀리는 경우가 많고 오류가 많이 난다. 그래서 이번 기회에 Bound에 대해서 정리 하려고 한다.
Binary Search
이진 탐색은 가장 유명한 탐색 기법이다.
만들기도 쉽고 직관적이다.
아주 쉬운 내용이기 때문에 간단히만 설명 하겠다.
Target이 3이고 길이 6의 array가 있다. 3을 찾기 위해서는 $ O(N) $으로 왼쪽에서 오른쪽으로 값을 찾는 방법도 있지만 Binary Search를 하면 $ O(logN) $ 으로 처리가 가능하다.
이를 처리하기 위한 핵심은 mid를 찾는데 있다.
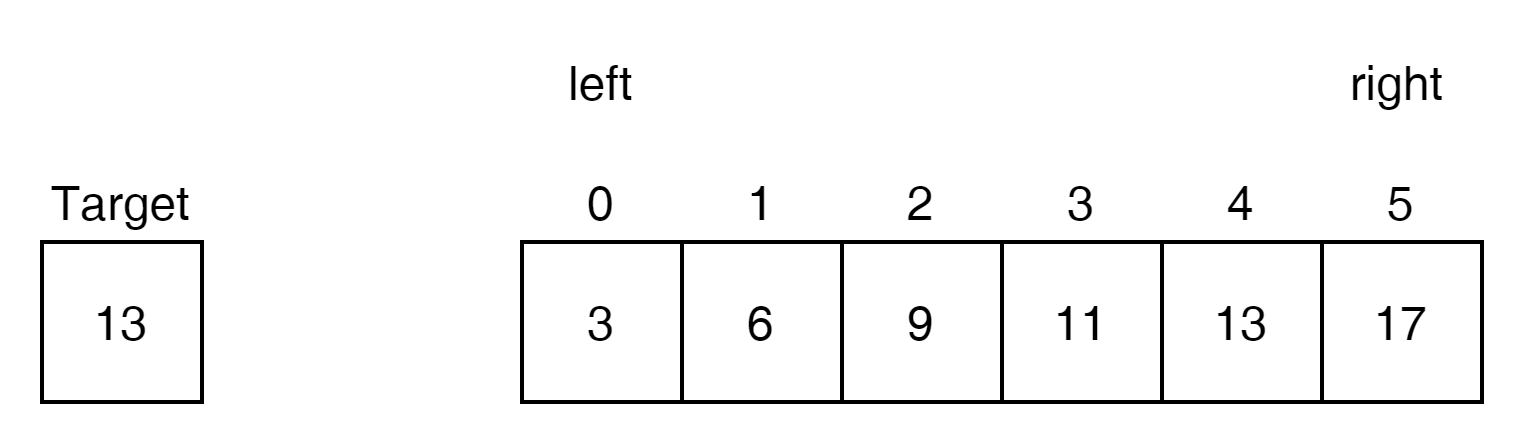
일반적인 mid를 찾는 기법은
let mid = Math.floor(left + (right - left) / 2);이다.
여기 나오는 mid와 Target이 같다면 결과값을 return 하면 된다.
결과 값이 나올수 있는 Target의 index 범위는
- 0 ~ length - 1 까지 이다.
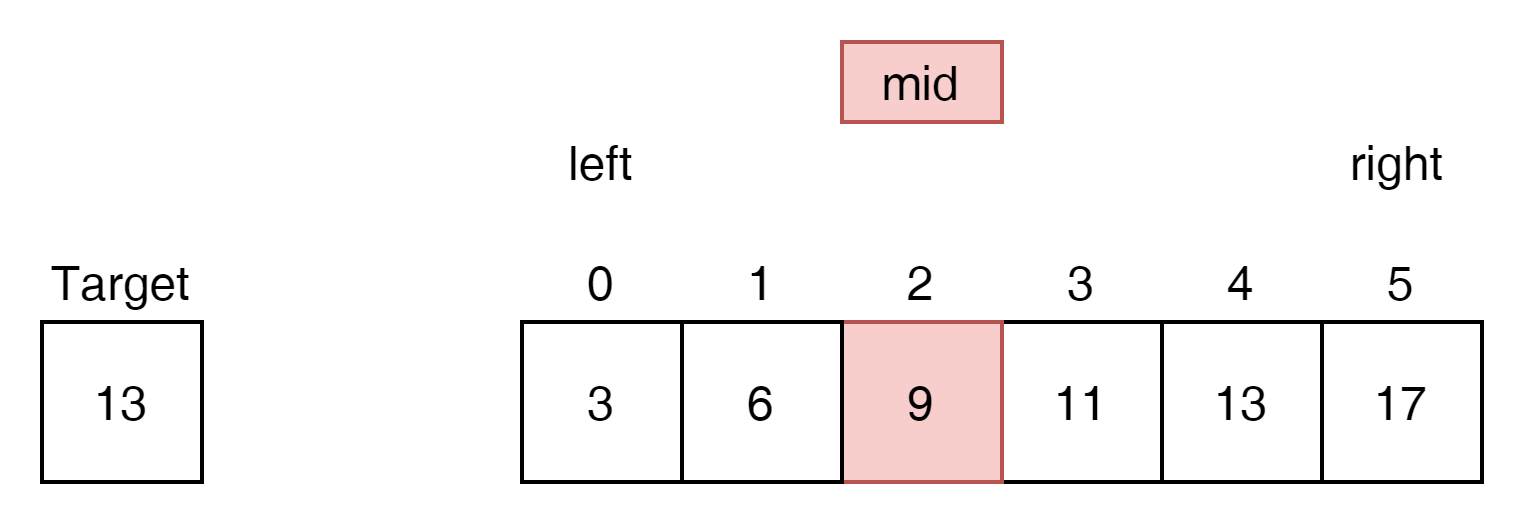
mid인 9는 13보다 작음으로 절대 답이 될 수 없다.
mid왼쪽으로는 답이 될 수 없는 영역임으로 left의 위치를 해당 영역밖으로 옮겨준다.
- left = mid + 1

5번째 index와 3번째 index 중간이 4번째 index에서 Target 값을 찾게 되었다.
Target을 좀 낮게 바꾸어 보자.

3을 찾아야 하는데 mid값인 9는 3보다 작음으로 9오른쪽은 모두 답이 될 수 없다.
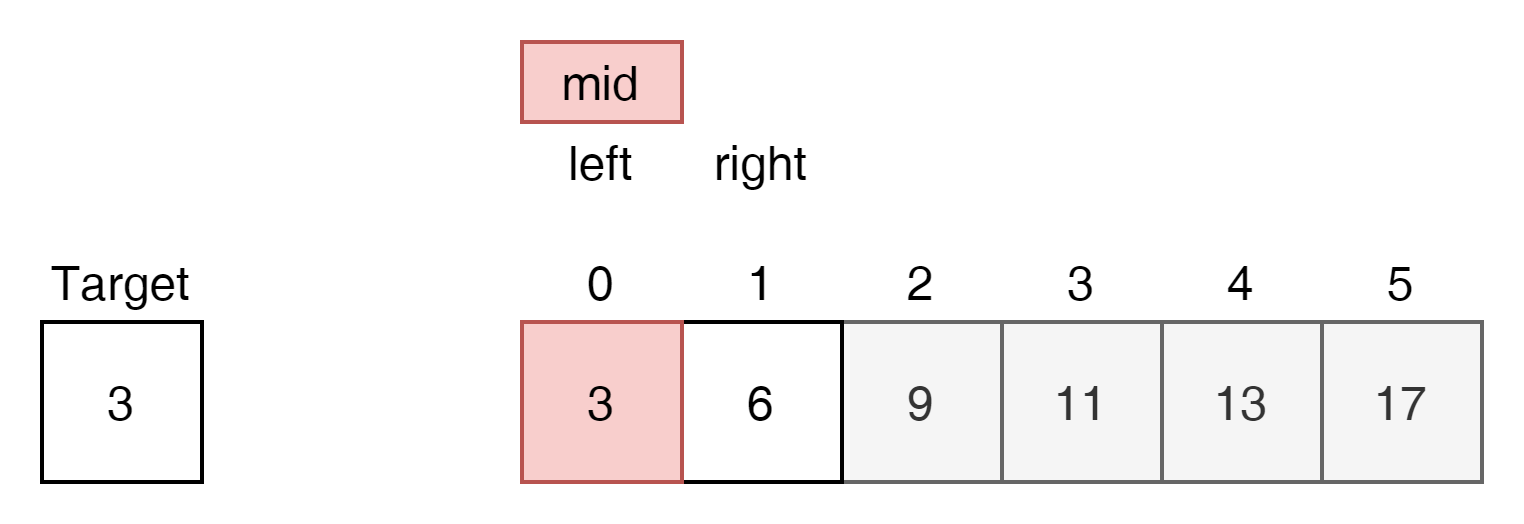
right를 mid 오른쪽 영역에서 벗어나게 하고 다시 mid를 찾아서 3이라는 value를 갖는 index를 찾았다.
- right = mid - 1
상기 내용을 코드로 바꾸어 보면 아래와 같다.
//같은 값 찾기
function binarySearchExat(target, arr) {
let left = 0;
let right = arr.length - 1; // right가 답이어도 out of index가 나지 않게
while (left <= right) {
let mid = Math.floor(left + (right - left) / 2);
if (arr[mid] < target) {// target이 더 큼으로 left를 mid로 올려야함
left = mid + 1; // left가 더 작다는게 확정임으로 + 1
} else if (arr[mid] > target) {
right = mid - 1; // right가 더 크다는게 확정임으로 - 1
} else {
return mid; //같은 값을 찾았음
}
}
return -1;
}
Binary Search Lower Bound
내가 목표하는 값이 들어갈 수 있는 가장 왼쪽 범위 index를 찾는게 문제이다.
Insertion Sort를 구현할때 자주 사용한다.
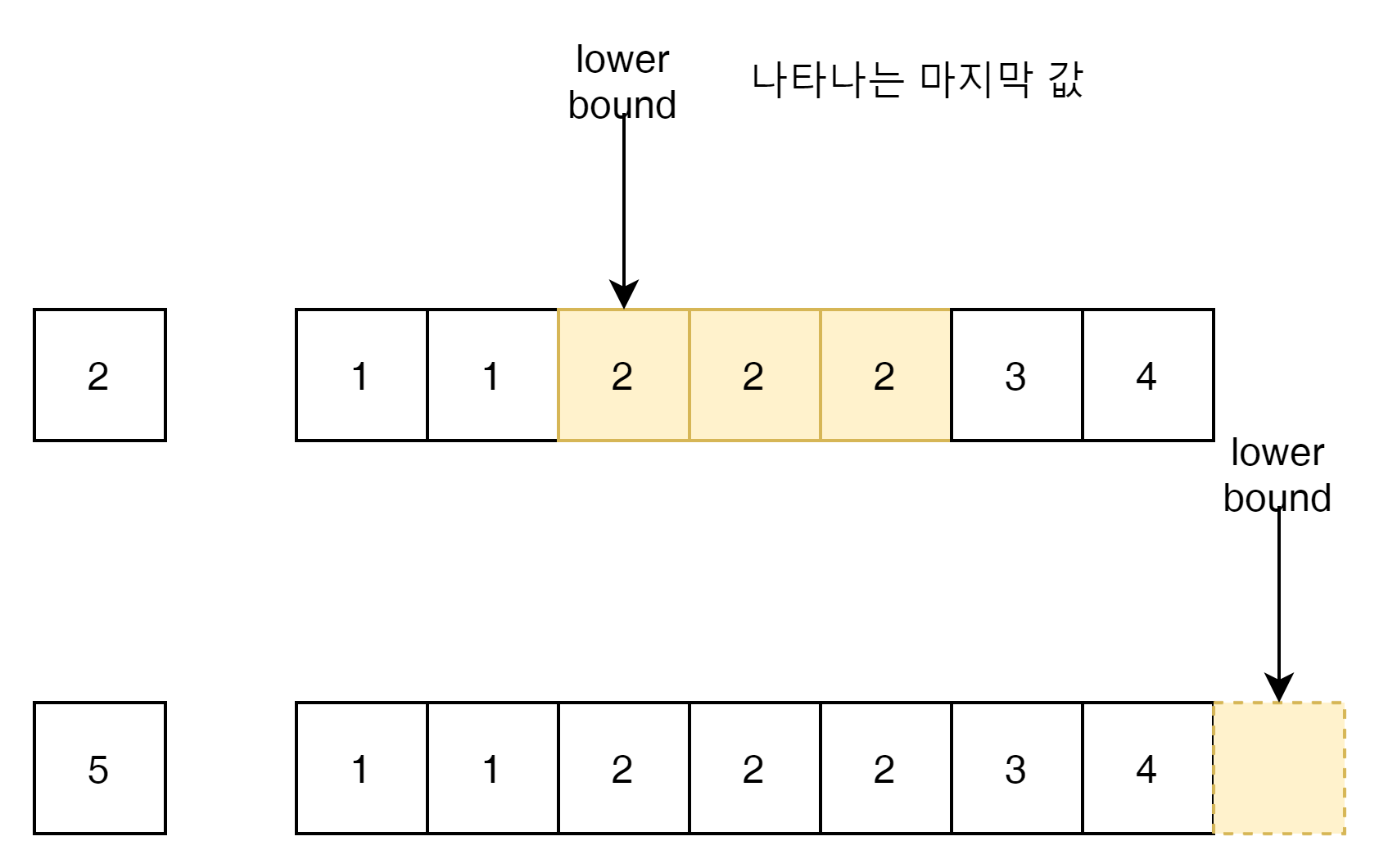
만약에 2라는 값을 Array에서 위치를 찾는다고 하면, 2보다 작은 값 바로 뒤에오는 직전 값이 목표 index가 된다.
위 그림에서는 3개의 2가 있는데 이중에서도 가장 왼쪽에 위치하는 2가 나와야 한다.
아래 그림은 5가 목표한 값인데 5가 없음으로 가장 직전의 낮은 값인 4뒤에 5의 위치가 나오게 된다.
이 그림을 보고 포인트를 몇가지 잡자면 다음과 같다.

- 답이 나올수 있는 범위는 0 ~ array length + 1 이다
즉 lower bound의 답이 array의 범위를 벗어 날 수 있다는 것이다.

답은 누가 되어야 할까?
최소한 되지 않아야 할것은 명확하다

- Target 값보다 낮은 값은 답이 될 수 없다.
- 즉, if array[mid] < target then left = mid + 1
그 외의 경우는 모두 답이 될수 있는 자격이 생기게 된다.
- if target <= array[mid] then right = mid
답이 절대로 되어선 안되는 범위와 답이 가능한 범위를 분리 해서 생각해야 한다.
마지막으로
- 목표 결과값은 left 이다
이 것을 코드로 만들면 아래와 같다.
//lower bound 찾기
function binarySearchLower(target, arr) {
let left = 0;
let right = arr.length; //lower bound가 arr의 길이를 넘어 갈 수 있음
while (left < right) { // left가 right와 같아 지게 되면 out of index가 될 수 있음
let mid = Math.floor(left + (right - left) / 2);
if (target <= arr[mid]) { //target과 같거나 target보다 딱 한단계 높은 mid를 찾음
right = mid; //같거나 한단계 높은것 자체가 답이 가능함 mid의 값을 옮길 순 없음
} else {
left = mid + 1; //target보다 낮은 값은 답이 될 수 없다 mid에서 늘려야 한다.
}
}
return left;
}
Binary Search Upper Bound
Target보다 큰 첫번째 위치를 찾는 것을 목표로 한다.

답이 될 수 있는 범위는
- 0 ~ array length + 1
이 된다.
즉, 위 예에서 보면 5가 target일때 해당 Array에 답이 없다면 마지막 위치인 array + 1의 위치가 답이 되어야 하기 때문이다.
그럼 절대로 답이 되어서 안되는 범위는 어디일까?

바로 자기 자신을 포함한 왼쪽은 모두 답이 될 수 없다.
- if array[mid] <= target then left = mid + 1
반대로 target보다 큰 값은 답의 대상이 된다.

- if array[mid] > target then right = mid
마지막으로
- left가 결과 값이다.
//upper bound 찾기
function binarySearchUpper(target, arr) {
let left = 0;
let right = arr.length; //upper bound가 arr의 길이를 넘어 갈 수 있음
while (left < right) { // left가 right와 같아 지게 되면 out of index가 될 수 있음
let mid = Math.floor(left + (right - left) / 2);
if (target >= arr[mid]) { //target보다 높은 값이 답이기 때문에 target이 더 크거나 target과 같다면 답이 될 수 없다.
left = mid + 1; //mid보다 커야한다.
} else {
right = mid; //mid가 target보다 커야 답이 가능함으로 mid는 답이 가능함으로 right를 욺지 이지 않는다
}
}
return left;
}
매번 비슷한 문제가 나올때마다 상위 Bound 계산으로 많이 혼동이 되는데 다음 3가지만 기억하자.
- Array의 범위를 넘어선 index가 답이 될 수 있는가?
- 절대로 답이 되어서 안되는 범위는 어디인가?
- left의 값을 증가 시켜라.
- median을 만드는 범위가 1,2 일경우 1을 선택함으로 무한 루핑에 빠지는 것을 피해라.
- 결과 값으로 return되는 것은 left 이다.
이렇게 기억하면... 좀 도움이 되겠지...
문제 풀이에 적용하기
Find First and Last Position of Element in Sorted Array
이 문제는 특정 Target값의 Upper Bound와 Lower bound를 찾는 문제이다.
문제 내용
Input: nums = [5,7,7,8,8,10], target = 8
Output: [3,4]위와 같이 문제가 주어 졌을때, 8은 3번 Position에서 시작해서 4번 Position으로 끝나게 된다.
접근 방법
Lower Bound 구하기
이건 완전히 위에 설명한 코드와 동일하게 작성하면 된다.
left = 0;
right = nums.length;
while(left < right){
int median = left + (int)Math.floor((right - left)/2);
if(target > nums[median]){
left = median + 1;
} else {
right = median;
}
}
Upper Bound만 조금 다른다.
우리가 찾기로한 대상은 Target 값이 된다. Target값보다 하나 더 높은 경계를 찾는 목적은 아니다.
그래서 Target보다 높은곳을 찾고 그곳보다 바로 아래 한단계가 답이 될 수 있다.
int left = 0;
int right = nums.length;
int[] result = new int[2];
while(left < right){
int median = left + (int)Math.floor((right - left)/2);
if(nums[median] <= target){
left = median + 1;
} else {
right = median;
}
}
if(0 == left || nums[left-1] != target) return new int[]{-1,-1};이 두개를 하나로 합치면 정답을 만들 수 있다.
class Solution {
public int[] searchRange(int[] nums, int target) {
if(nums.length <= 0) return new int[]{-1,-1};
int left = 0;
int right = nums.length;
int[] result = new int[2];
while(left < right){
int median = left + (int)Math.floor((right - left)/2);
if(nums[median] <= target){
left = median + 1;
} else {
right = median;
}
}
if(0 == left || nums[left-1] != target) return new int[]{-1,-1};
result[1] = left-1;
left = 0;
right = nums.length;
while(left < right){
int median = left + (int)Math.floor((right - left)/2);
if(target > nums[median]){
left = median + 1;
} else {
right = median;
}
}
result[0] = left;
return result;
}
}'Problem Solving' 카테고리의 다른 글
| Longest Increasing Path in a Matrix (0) | 2021.06.23 |
|---|---|
| Count of Smaller Numbers After Self (0) | 2021.06.23 |
| Remove Invalid Parentheses (0) | 2021.06.14 |
| Regular Expression Matching (0) | 2021.06.13 |
| Critical Connections in a Network (0) | 2021.06.11 |
