Longest Increasing Path in a Matrix
문제 내용
Matrix에서 오름차순으로 갈수 있는 최대의 길이를 구하라
접근 방법
음... 오랫만에 쉬운문제라 행복했다.
dfs만으로 해결이 된다.
Matrix가 M x N 이라고 할때 하나의 cell을 한번만 순환하게 만들면 된다.
예를 들어보면

상기 문제에서 $ (1,0) $에는 4가 들어있다. 4에서 오름차순이 가능한 cell은? 없다.
dp로 보면 자기 자신만이 가능함으로 1의 길이를 갖는다.

이 길이는 확정이 된다.
그럼 $ (1,1) $ 은 어떤가?
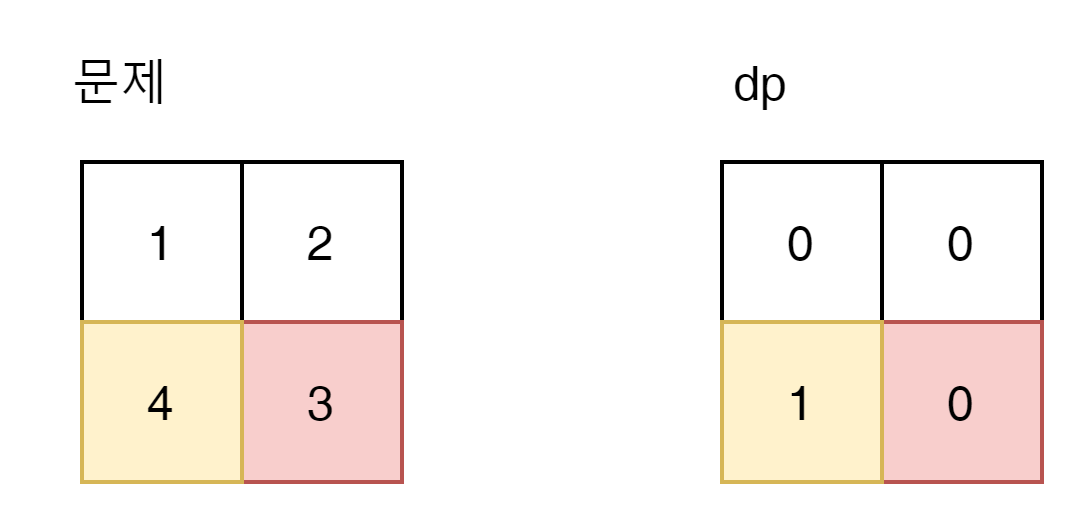
4로만 오름차순으로 올라갈 수 있다. 하지만 4는 이미 dp의 값이 확정이다. 4로 순회 할 필요 없이 4의 dp 값 1에 자기 자신 1을 더하면 된다.
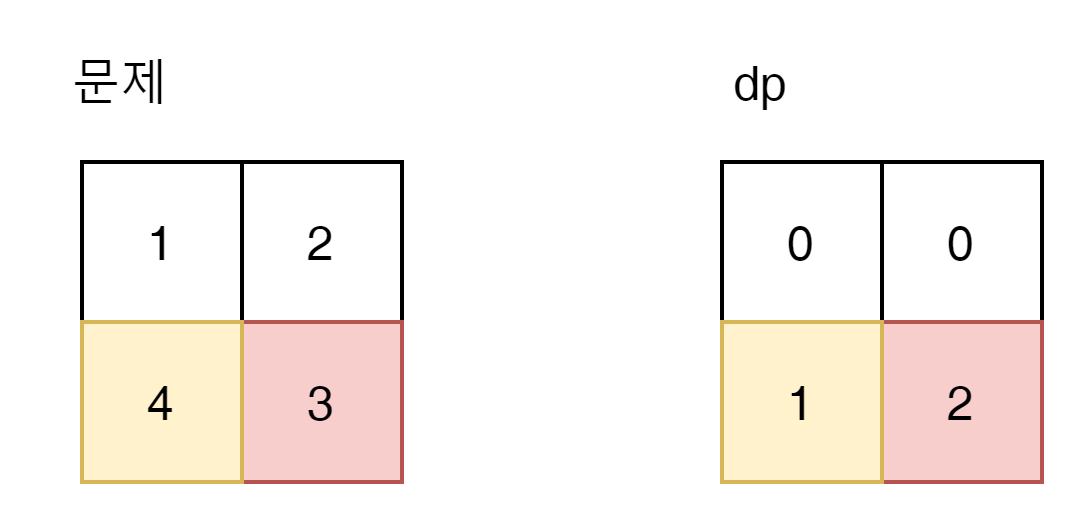
2는 어떤가? 3으로밖에 갈수 없다.

dp는 3이된다.
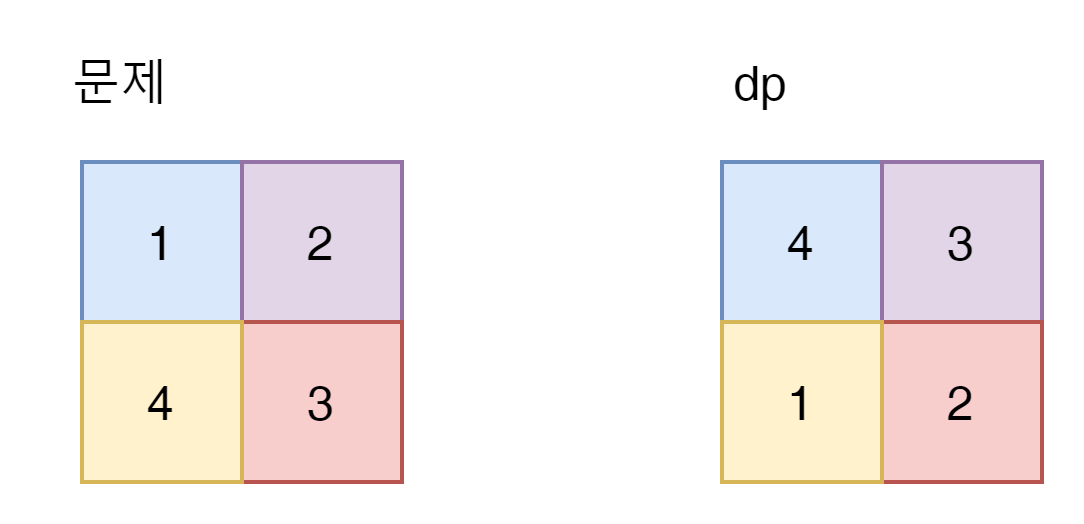
마지막으로 1은 4또는 2로 갈수 있는 선택권이 있다.
이중에 가장 많이 갈수 있는 max length를 선택하면 된다.
$ (0,1) $ 이 3이라는 dp값을 갖음으로 해당 cell 즉 문제의 2라는 값을 갖는 cell을 선택하면 된다.
Time complexity는 dp로 인해서 한번만 순회 함으로
$$ O(M*N) $$ 이 된다.
var longestIncreasingPath = function(matrix) {
let result = 0;
let rows = matrix.length;
let cols = matrix[0].length;
let dp = new Array(rows).fill(0).map(_ => new Array(cols).fill(-1));
for (let row = 0; row < rows; row++) {
for (let col = 0; col < cols; col++) {
dfs(matrix, dp, row, col);
result = Math.max(result, dp[row][col]);
}
}
return result;
function dfs(matrix, dp, row, col) {
// console.log(row, col);
if(-1 < dp[row][col]) return dp[row][col];
let rowDir = [-1,0,1,0];
let colDir = [0,1,0,-1];
let max = 1;
for (let i = 0; i < 4; i++) {
if (0 <= row + rowDir[i] && 0 <= col + colDir[i] && row + rowDir[i] < rows && col + colDir[i] < cols ) {
max = Math.max(max, matrix[row][col] < matrix[ row + rowDir[i] ][ col + colDir[i] ] ? dfs(matrix,dp, row + rowDir[i], col + colDir[i]) + 1 : 0);
}
}
dp[row][col] = max;
return max;
}
};728x90
반응형
'Problem Solving' 카테고리의 다른 글
| Greatest common divisor (gcd) 최대 공약수 구하기, Euclidean algorithm 유클리드 알고리즘 (0) | 2021.06.27 |
|---|---|
| Reaching Points (0) | 2021.06.26 |
| Count of Smaller Numbers After Self (0) | 2021.06.23 |
| Binary Search Lower Bound와 Upper Bound (0) | 2021.06.17 |
| Remove Invalid Parentheses (0) | 2021.06.14 |
