문제 내용
(sx,sy)로 시작한 point는 다음과 같이 값을 변화 시킬 수 있다.
- (sx + sy, sy)
- (sx, sy + sx)
최종값이 (tx,ty) 가 가능한가?
접근 방법
기본 적인 접근법은 Binary Node를 확장하는 것이다.

(sx, sy)가 (1,1)일 경우 sx를 증가 시키거나 sy를 증가시키거나 하는 방법으로 $ 2^n $ 으로 node를 늘려가면서 정답을 찾으면 된다.
그러나 이것은 매우 비효율 적이다.
만약에 tx, ty가 (2,3)이라고 생각해 보자.

back ward로 거슬러 올라오는 방식으로 접근을 한다면, 가지 치기가 되게 된다.
이 가지 치기를 할때 한가지 rule만 따르면 된다.
- 큰곳에서 작은 것을 뺀다.
왜냐면 작은것에서 큰것을 빼면 음수값이 나오게 되어서 종료 되기 때문이다.
이것을 Time complexity로 생각해 보면
$ O( max(tx,ty) ) $ 가 된다.
예를 들어서 (1,1)에서 시작해서 (1,10000)를 만든다고 생각하면,
(1,10000)에서 ty인 10000을 9999번 빼기를 하면 된다.
즉, tx와 ty중 큰 값의 횟수를 넘어가지 않게 된다. 가장 최악의 경우를 생각해도
sx와 sy는 1보다 크게 된다.
그러나 이것도 TLE가 나게 된다. 어떻게 더 최적화 해야할까?
위에서 9999번 빼기를 해야한다고 했는데, 이부분을 이용해 보자.

sy는 고정되어 있고 sx에 sy를 지속적으로 올리는 경우이다.
이경우는 다음 공식이 만족되게 된다.
$$ 0 == (tx - sx) % ty $$
반대의 경우를 보자.
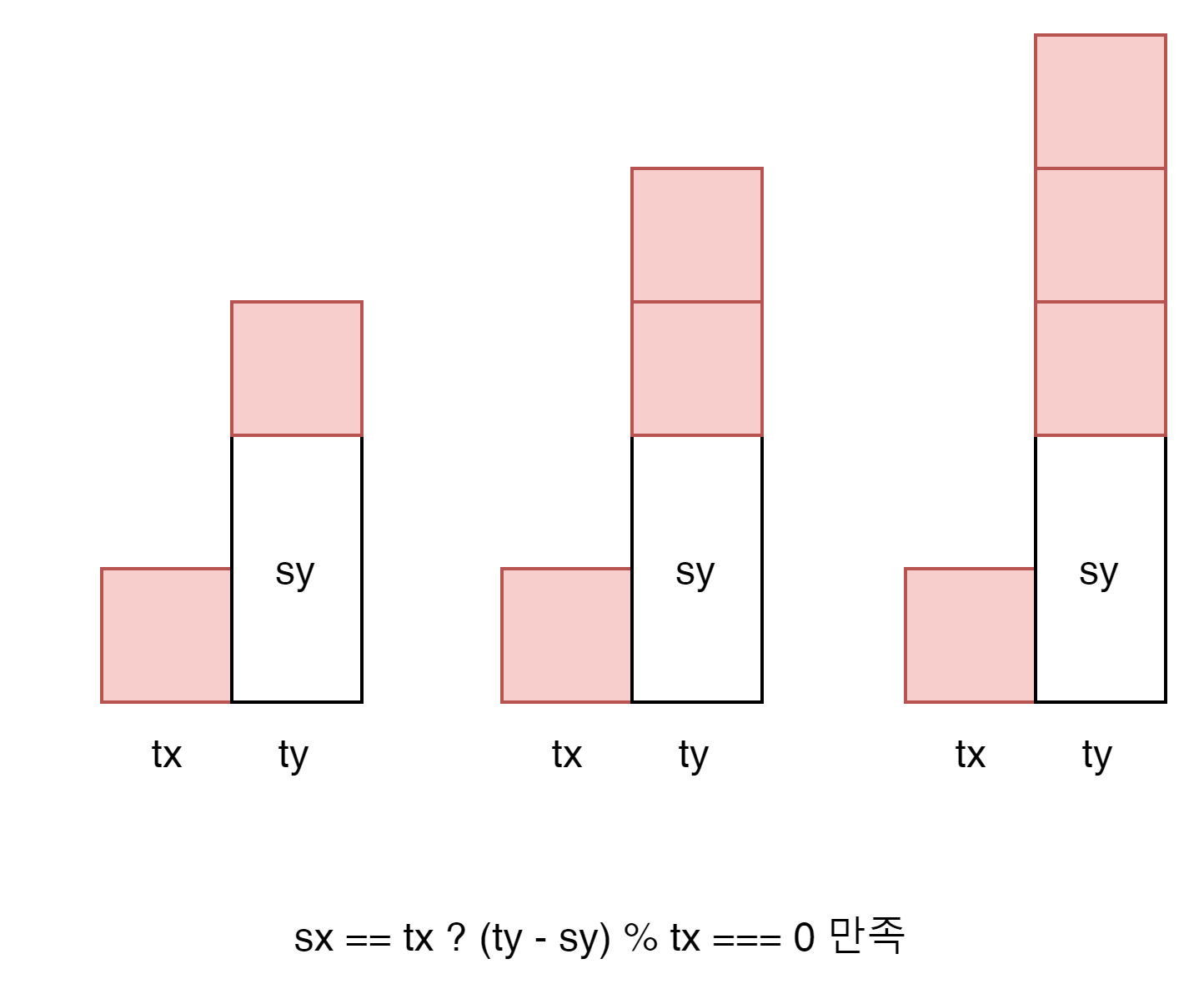
역시
$$ 0 == (ty - sy) tx $$
의 공식을 산출 할 수 있다.
그러면이제 이 두가지 경우가 섞이는 경우면 어떻게 될까?

tx에 sy를 올리고 ty에 tx를 올려보자.
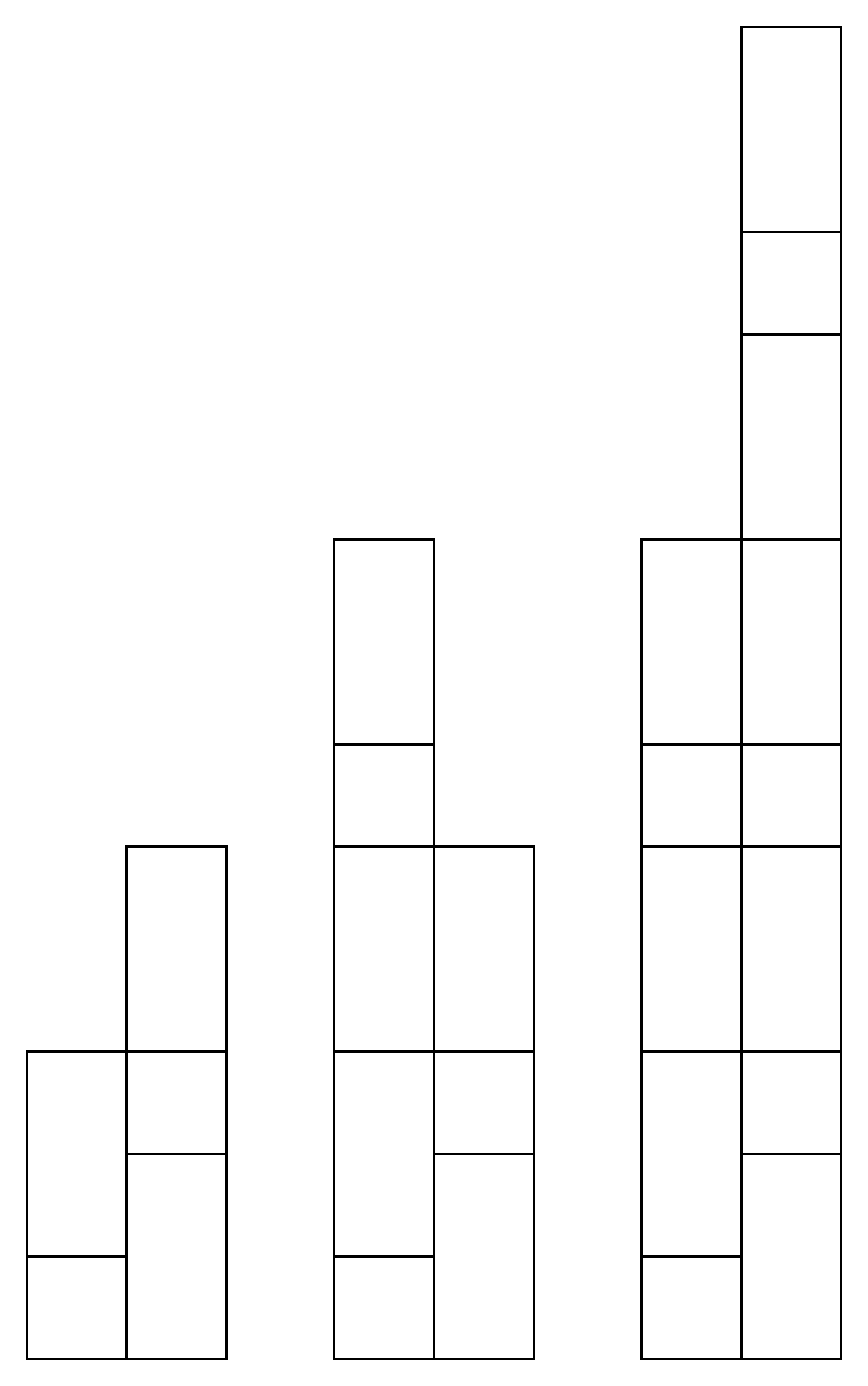
이런식으로 tx와 ty의 값은 지속적으로 키워 나가게 된다.
그럼 이제 다시 원상 복귀를 해보자

최종 값에서 ty가 더 큰 값이됨으로 tx를 마이너스 한다. 물론 한번이 될 수도 있지만 여러번이 될수도 있음으로 modulation을 사용하자.
$$ ty % tx $$
이런식으로 값을 줄여나가면 아래 그림과 같이 되게 된다.
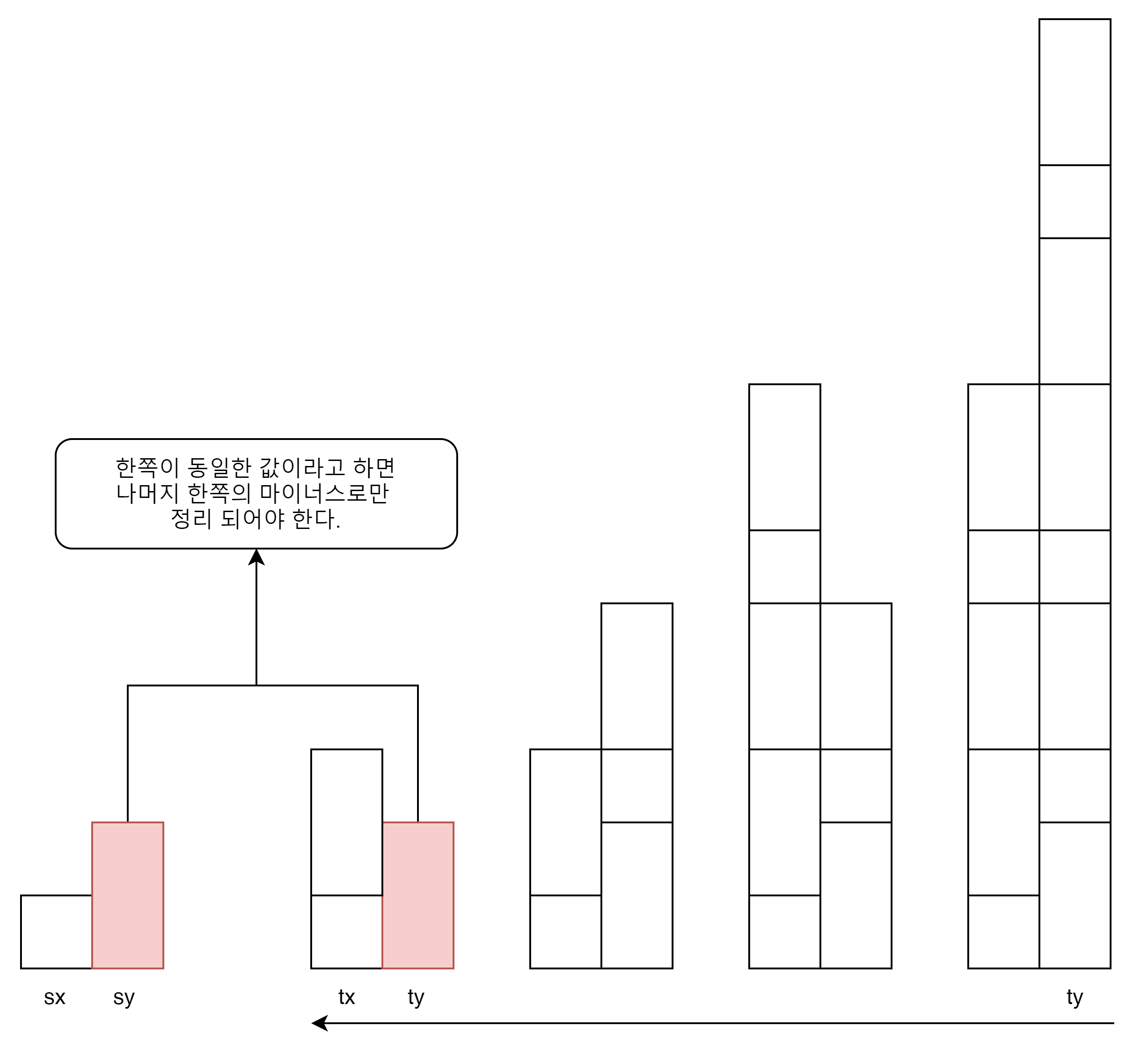
가장 큰값에서 작은값을 modulation 처리하면서 sx와 sy의 값 둘중에 하나의 값과 같을때 까지 이 행위를 연속적으로 진행한다.
이것을 코드로 보면 아래와 같다.
while(sx < tx && sy < ty){
if(tx < ty) ty = ty % tx; //tx와 ty의 높이를 역전시킨다
else tx = tx % ty
}한쪽의 값이 고정되었음으로 앞서 설명한 modulation을 통해서 값을 정리한다.
if(sx === tx && sy <= ty){ //x가 고정이 된다면 y는 -sy를 제외한 값이 x의 배수로 만들어 져야 한다.
return (ty - sy) % sx === 0;
}
if(sy === ty && sx <= tx){ //y가 고정이 된다면 y는 -sx를 제외한 값이 y의 배수로 만들어 져야 한다.
return (tx - sx) % sy === 0;
}주의해야 할 것은
- 한쪽값이 고정되어있으면 나머지 한쪽값은 반듯이 target값과 같거나 더 작아야 한다.
이것을 코드로 만들면 아래와 같다.
var reachingPoints = function(sx, sy, tx, ty) {
while(sx < tx && sy < ty){
if(tx < ty) ty = ty % tx; //tx와 ty의 높이를 역전시킨다
else tx = tx % ty
}
if(sx === tx && sy <= ty){ //x가 고정이 된다면 y는 -sy를 제외한 값이 x의 배수로 만들어 져야 한다.
return (ty - sy) % sx === 0;
}
if(sy === ty && sx <= tx){ //y가 고정이 된다면 y는 -sx를 제외한 값이 y의 배수로 만들어 져야 한다.
return (tx - sx) % sy === 0;
}
return false;
};mod는 O(1)의 operation으로 볼수 있고, 한쪽의 나누기로 값을 나누어 감으로
$$ O(log max(tx,ty)) $$
로 대략적인 Time Complexity를 볼 수 있다.
하지만 정확한 해석은 다음 Article을 참조하자.
https://www.geeksforgeeks.org/time-complexity-of-euclidean-algorithm/
'Problem Solving' 카테고리의 다른 글
| Max Points on a Line (0) | 2021.06.27 |
|---|---|
| Greatest common divisor (gcd) 최대 공약수 구하기, Euclidean algorithm 유클리드 알고리즘 (0) | 2021.06.27 |
| Longest Increasing Path in a Matrix (0) | 2021.06.23 |
| Count of Smaller Numbers After Self (0) | 2021.06.23 |
| Binary Search Lower Bound와 Upper Bound (0) | 2021.06.17 |
