사람이 최대 공약수를 구하는 방법은 다음과 같은 계산 방식으로 해결을 한다.

그럼 프로그램 적으로는 어떻게 접근 하는 것이 좋은가?
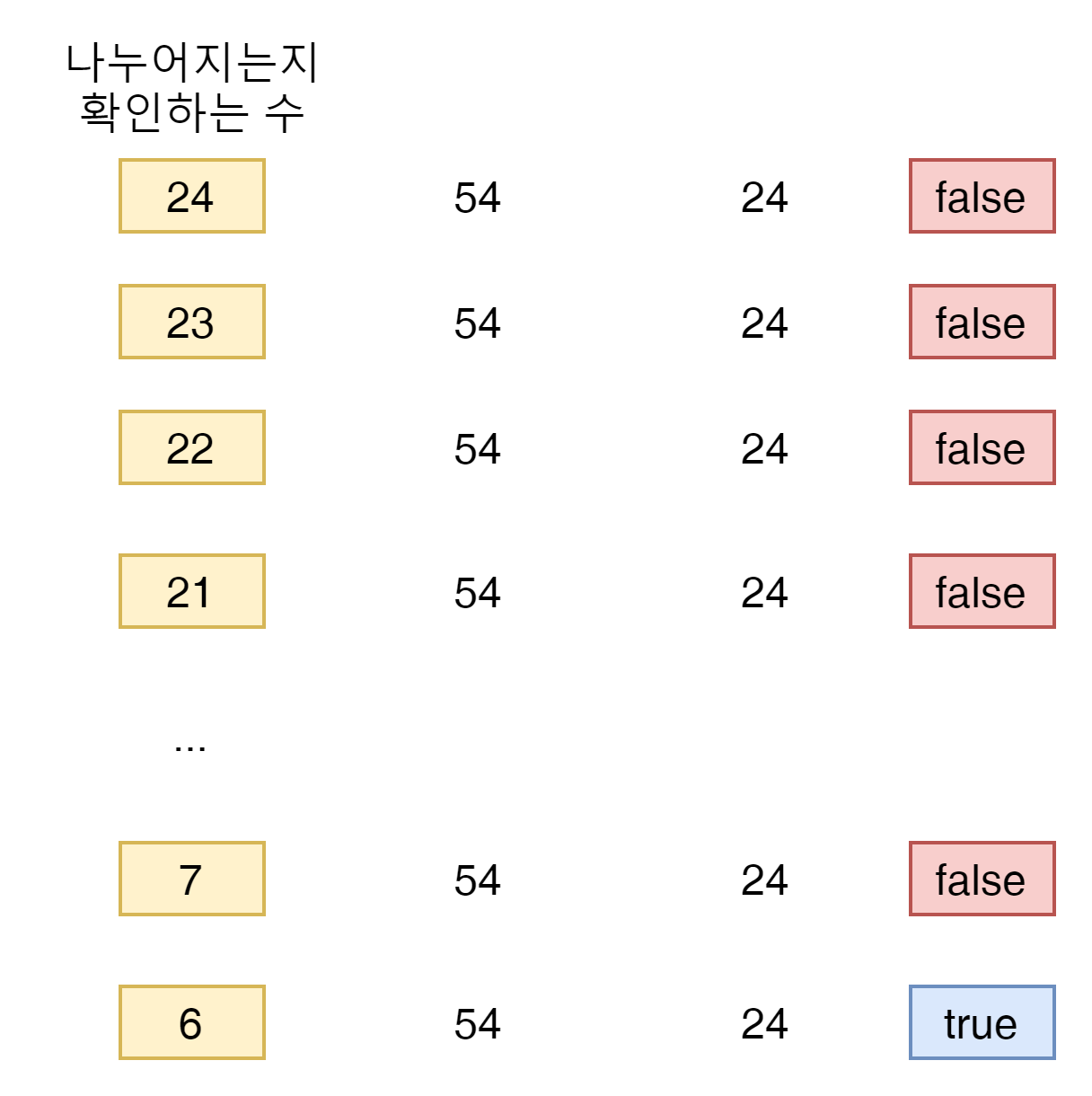
모든 경우의 수를 계산 한다.
최대공약수는 기본적으로 a와 b를 동시에 나눌 수 있는 가장 큰 수라는 전제가 있다.
그렇기 때문에 a와 b중 작은 수를 기준으로 모든 수를 나누어 보면 된다.
function gcd_linear(a, b) {
let min = Math.min(a, b);
for (let i = min; 0 <= i; i--) {
if(a % i === 0 && b % i===0){
return i;
}
}
return 1;
}프로그램으로는 상기와 같다.
이것을 Time complexity로 생각해 보면 $$ O(min(a,b)) $$ 가 된다.
하지만 그 숫자가 굉장히 커지게 되면 비효율적인 방법이 된다.
Euclid's algorithm
Euclid의 정리에 따르면 다음과 같은 공식이 성립한다고 한다.
a와 b라는 값이 주어졌고 둘중에 더 큰 값을 a라고 했을때,
(a - b, b) 가 가능하고 계산된 결과가 같다면 해당 같은 값을 최대 공약수라고 할 수 있다.
예를 들어보면 다음과 같다.
(48,18) -> (48-18, 18) -> (30, 18) -> (30 -18, 18) -> (12, 18) -> (12, 18 - 12) -> (12, 6) -> (12 - 6, 6)
-> (6,6)
6이 GCD가 된다.
이것이 왜 가능한지 증명하는 것은 이글을 쓰고 있는 나도 이해가 잘 안되어서,
다른 사이트를 찾아 보는 것이 좋겠지만 나름대로 다음과 같이 설명은 가능하다.
- 0이상의 소수점이 없는 두개의 수가 있을 때 무조건 하나이상의 최대 공약수는 존재한다.

1과 3이 주어졌을 때 무조건 일의 최대 공약수는 존재 할 수밖에 없다.
그럼 이 전재를 갖고 다음 값을 보자.

답은 당연하게도 3이 될것이다.
만약에 우리가 컴퓨터라고 생각해보자. 컴퓨터는 직관적으로 3이 답이라는 것을 알 수 없다.
대신에 이것은 알 것이다.
- 어떤 값인지는 모르겠지만 3과 9에 최대 공약수는 무조건 존재한다.
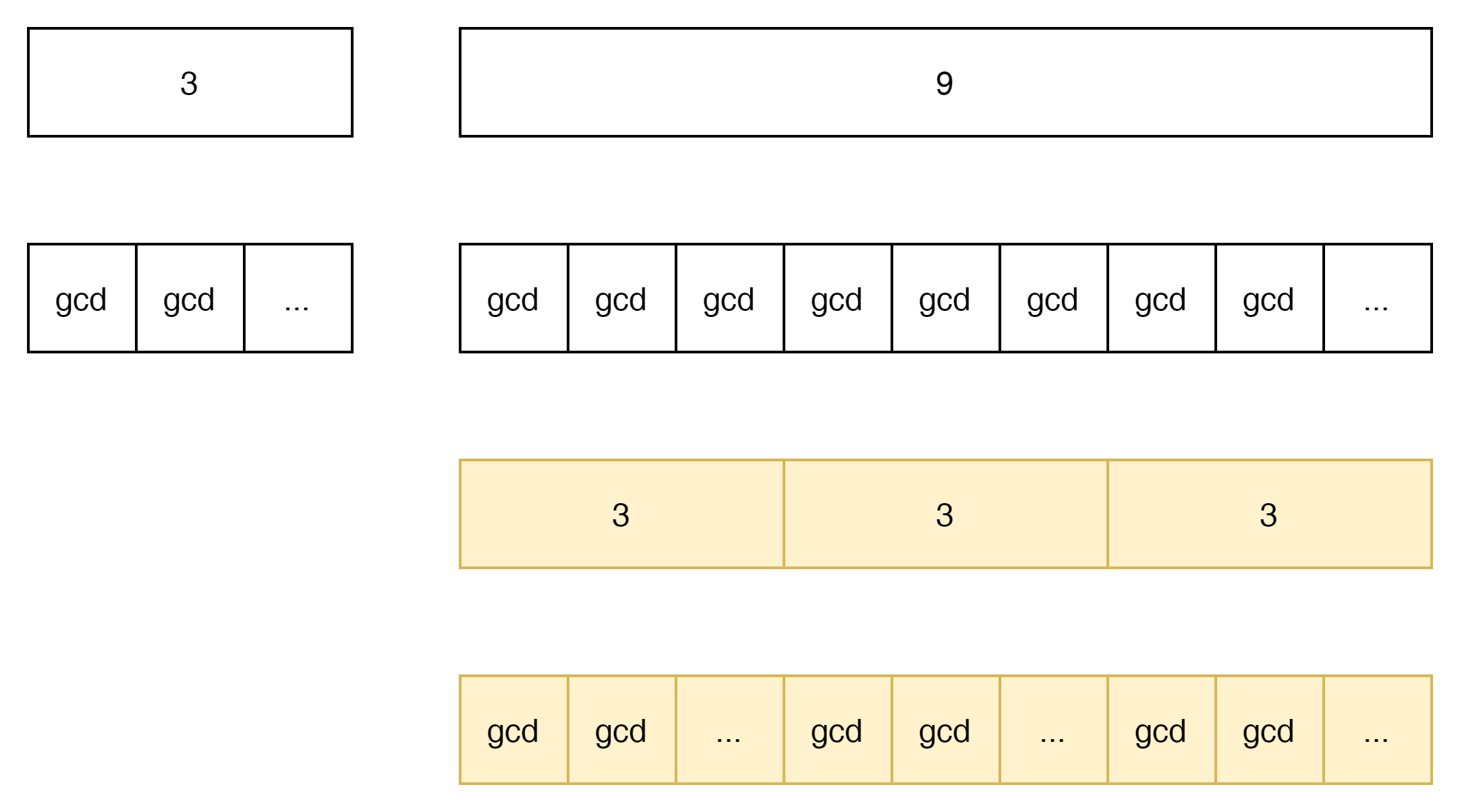
이것을 그림으로 나타내 보자.

3은 몇인지 모르지만 최대공약수 gcd의 합으로 구성될 수 있다.
9는 몇인지 모르지만 최대 공약수 gcd의 합으로 구성될 수 있다.
그럼 다음의 내용도 성립할 수 있다.

9 = 9 - 3을 해도 gcd 라는 값이 변동되지 않는 다는 것이다.
- GCD가 두개의 Value는 큰 값에서 작은 값을 빼도 GCD 갯수에는 변화가 없다.
- 즉, GCD의 크기에 대한 변화도 없다.
이것을 연속적으로 나타내 보자.

상기 그림을 보면 최종적으로 남늠 gcd는 3인것을 알 수 있다.
- GCD는 한쪽이 0이 될 때까지 빼서 남는 값이 최대값이 된다.
function gcd_minus(a, b) {
if(a === 0 || b === 0) return a + b;
if (a < b) {
return gcd_minus(a, b - a);
} else {
return gcd_minus(a - b, b);
}
}Time complexity는 모든 경우의 수보다 평균적으로 빠르겠지만 big O 관점에서는 동일한 속도를 나타낸다.
$$ O(min(a,b)) $$
Euclid's algorithm을 최적화 해보자.
Euclidean algorithm
드디어 유클리드 알고리즘 또는 유클리드 호제법이라고 불리우는 것에 대해서 알아보자
이 방법은 상기에 있는 Euclid's Algorithm을 Modulation을 통해서 조금 더 최적화 시킨 방법이다.
앞서서 큰값은 작은 값의 빼기로 나타낼 수 있다고 했다.
이것을 그림으로 그려 보자면 아래와 같다.
9는 3개로 이루어진 최대 공약수로 나타낼 수 있다.
만약에 이것을 조금더 꼬아보면 어떨까?

12는 9로 구성 될 수 있다는 것을 이제는 이해가 가능할 것이다.

12를 작은수 9로 빼고 나면 결국 앞서 만든 문제인 3과 9로 이루어진 문제가 된다.
이제 3을 3번 빼고 나면 답이 3으로 나올 것이라는 것을 우리는 안다.
여기서 무었을 최적화 시킬 수 있을까?
- 9를 3으로 모듈레이션 하면 어떨까?
즉, 9 % 3이면 9는 0이 되고 3이 답이 된다.
Modulation은 $ O(1) $로 추정을 하면 굉장히 빠른 속도로 문제 해결이 가능하게 된다.

이것을 프로그램으로 작성해 보자.
function gcdRcu(a, b) {
if(b === 0) return a;
else return gcdRcu(b, a % b);
}Modulation의 특성을 생각해보면 Modulation이 된 값은 항상 Modulation 한 값보다 작은 값이 된다.
만약에 상기 그림에서 b가 a보다 크다고 해도 문제는 없다. 결국 다시 ( b,a) 가 될것이다.
반대로 b가 a보다 작다면?
그것은 b % a처럼 될 것이고 b는 a보다 작은 값이 될 수 밖에 없다.
상기 코드는 최종적으로 b가 0이 될 수밖에 없다. Modulation이 두번째 파라메터에서만 이루어지기 때문이다.
그럼 답은 a가 되게 된다.
Time complexity는 $$ O(log min(a,b)) $$ 가 된다고 한다.
정확한 Time Complexity는
https://www.baeldung.com/cs/euclid-time-complexity
을 참고 바란다. 아무리봐도... 이해가 안가서 ^^;;
간단해 보이는 코드이지만 깊이가 있는 알고리즘이다.
'Problem Solving' 카테고리의 다른 글
| The Skyline Problem (0) | 2021.06.30 |
|---|---|
| Max Points on a Line (0) | 2021.06.27 |
| Reaching Points (0) | 2021.06.26 |
| Longest Increasing Path in a Matrix (0) | 2021.06.23 |
| Count of Smaller Numbers After Self (0) | 2021.06.23 |
