문제 내용
어떤 1차 방정식의 선분을 그었을 때 해당 선을 지나가는 가능 많은 Points의 갯수를 구하라.
접근 방법
지극히 수학적인 접근이 필요하다.
우선 기본적인 1차 방정식을 생각해 보자.
$$ y = ax + b$$
여기에서 a는 기울기 b는 절편이라고 생각하면 된다.
기울기는 다음과 같이 나타낼 수 있다.

y의 변화량을 x의 변화량으로 나눈 값이 된다.
$$ slope = (y2 - y1) / (x2 - x1) $$
이것을 3개의 Point가 한개의 선을 지나가는가? 라는 접근 방법은 아래와 같이 나타낼 수 있다.
$$ (y2 - y1) = (x2 - x1) * slope + bias $$
그런데 위 수식에서 bias는 두점에 대한 상대라고 생각했을 때 bias는 전혀 필요가 없다는 것을 알 수 있다.
(1번점 bias - 2번점 bias = 0)
$$ (y2 - y1) = (x2 - x1) * slope $$
해당 수식에 slope를 추가해 보겠다.
$$ (y2 - y1) = (x2 - x1) * (y2 - y1) / (x2 - x1) $$
이 수식에서 이항을 하면,
$$ (y2 - y1) / (x2 - x1) = (y2 - y1) / (x2 - x1) = slope $$
이 되게 된다.
$$ y의 변화량 / x의 변화량 = (y2 - y1) / (x2 - x1) = (y2 - y1) / (x2 - x1) = slope $$
3번째 Point로 해당 값을 나타내면
$$ (y3 - y1) / (x3 - x1) = (y2 - y1) / (x2 - x1) = (y2 - y1) / (x2 - x1) = slope $$
즉, slope가 동일하면 해당 점들은 한 선위에 존재 한다고 생각해도 좋다.
그러면 bias는 진짜로 이 수식에서 신경쓰지 않아도 되는걸까?
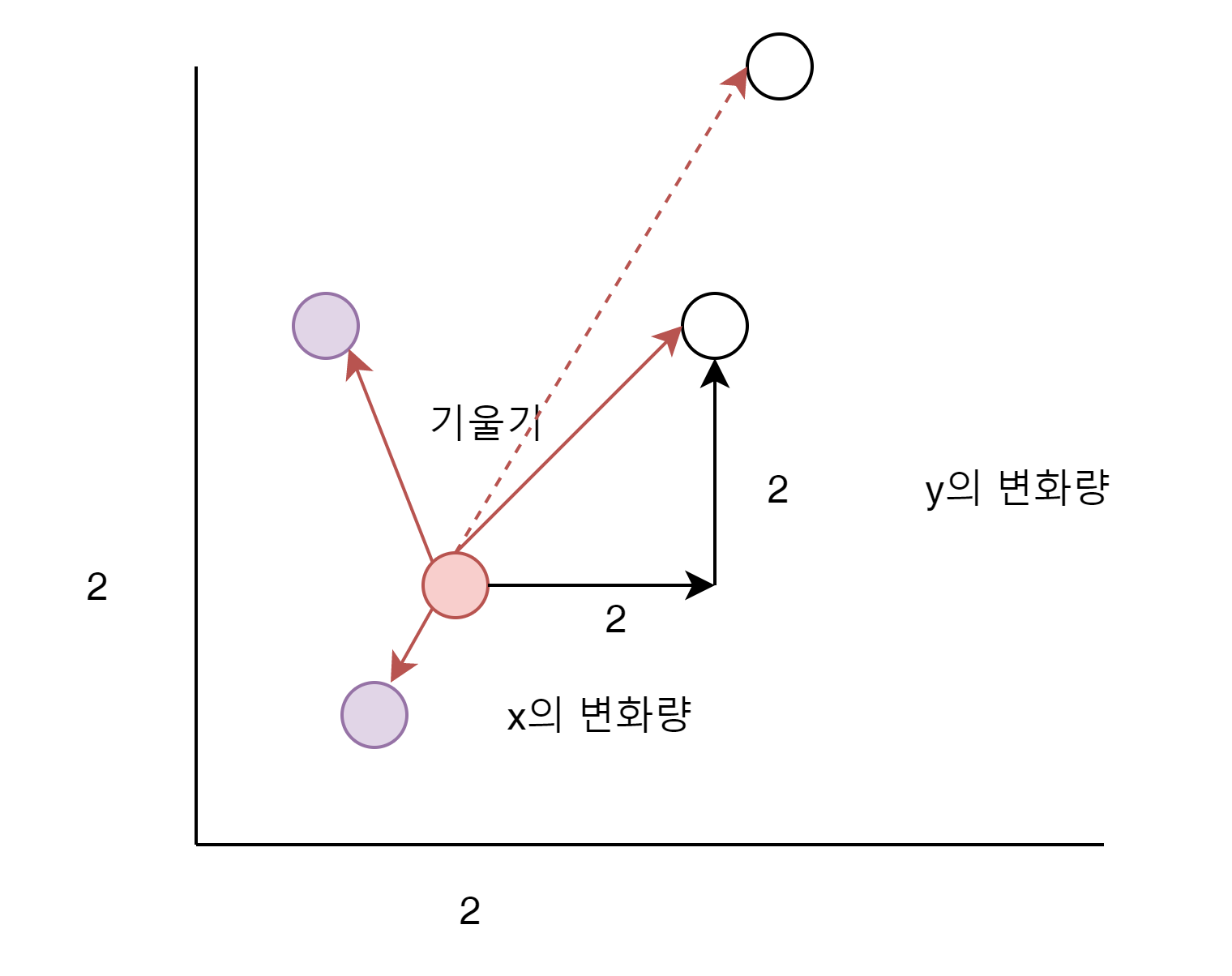
상위 그림을 보면 이해하기가 좋다.
(2,2)에서 출발하는 점에서 다른 점으로의 한 선을 그었을 때 관심 있는 것은 오직 기울기 뿐이다.
한 점에서 나갈수 있는 360개의 선분(예를 들어서)이 있다고 생각해 보면, 그 점에 연결되는 Target Point와의 Slope관계만 필요 한것이지, 절편인 Bias가 어디에 위치하는 지는 (2,2) 입장에서는 아무런 관심의 대상이 되지 않는다.
오직 Slope만 같아도 한 선 위에 있어도 된다고 생각할 수 있다.
이 아이디어를 바탕으로 Slope를 key로 하는 Map으로 Count를 해서 가장 많은 수를 구하면 될 것이라는 생각을 떠올릴 수 있다.
하지만 여기에서 문제가 하나 생긴다.
- Slope는 분수의 형태임으로 소숫점을 갖을 수 있다.
실수를 key로 하는 것은 개발하기 까다로운 문제이기 때문이다.
이것을 해결하기 위해서 변화량의 상대성을 한번 살펴볼 필요가 있다.

(2,2)에서 (4,3)까지 가는데 있어서의 slope 1/2 즉 0.5가 된다.
하지만 slope는 key로 사용되기 어렵다고 앞서 말을 하였다. 그럼 변화량 자체만을 보자.
- x의 변화량 2
- y의 변화량 1
을 확인 할 수 있다.
그럼 3번재 포인트인 (6,4)를 보자 slope는 2/4 즉 0.5로 한 선 위에 있다는 것을 알 수 있다.
변화량은 어떠한가?
- x의 변화량 4
- y의 변화량 2
이다. 변화량에 있어서 x와 y에 일정한 배수가 존재 한다는 것을 알 수 있다.
4와 2의 최대 공약수를 구하면?
2가 최대 공약수가 됨으로
- x변화량 2 = 4 / 2(gcd)
- y변화량 1 = 2 /2 (gcd)
(4,3)이 갖고 있는 변화량과 동일한 것을 알 수있다.
slope는 결국 x와 y의 상대적 연관율을 표시 한 것임으로 이것이 성립 가능하다.
이렇게 해서 키를 x의 최소 변화량, y의 최소 변화량 으로 나타낼수 있게 되었다.
Time Complexity는 한점에서 나머지점 모두를 순환하는 방식임으로
$$ O(N^2) $$ 이 된다.
/**
* @param {number[][]} points
* @return {number}
*/
var maxPoints = function(points) {
function Gcd(a,b){
if(b === 0) return a;
else return Gcd(b, a % b);
}
let maxResult = 0;
for (let i = 0; i < points.length; i++) {
let map = new Map();
let sPoint = points[i];
let max = 0;
let overlap = 0;
for(let j = i + 1; j < points.length; j++){
let tPoint = points[j];
let rationalX = tPoint[0] - sPoint[0];
let rationalY = tPoint[1] - sPoint[1];
if (rationalX === 0 && rationalY === 0) {
overlap++;
} else{
let gcd = Gcd(rationalX, rationalY);
rationalX /= gcd;
rationalY /= gcd;
if (map.has(rationalX)) {
let mapY = map.get(rationalX);
if (mapY.has(rationalY)) {
mapY.set(rationalY, mapY.get(rationalY) + 1);
} else {
mapY.set(rationalY, 1);
}
} else {
map.set(rationalX, new Map());
map.get(rationalX).set(rationalY, 1);
}
}
max = Math.max(max, map.get(rationalX).get(rationalY));
}
// console.log(map);
maxResult = Math.max(maxResult, max + overlap);
}
return maxResult + 1;
};
console.log(maxPoints([[2,2],[4,3],[6,4],[8,4]]));
'Problem Solving' 카테고리의 다른 글
| One Edit Distance (0) | 2021.07.05 |
|---|---|
| The Skyline Problem (0) | 2021.06.30 |
| Greatest common divisor (gcd) 최대 공약수 구하기, Euclidean algorithm 유클리드 알고리즘 (0) | 2021.06.27 |
| Reaching Points (0) | 2021.06.26 |
| Longest Increasing Path in a Matrix (0) | 2021.06.23 |
