문제 내용
평평한 선위에 직사각형으로 구성된 네모로 만들어진 그룹이 있다.
이것을 [start point,end point, height]의 집합으로 표현한다고 했을 때,
겹친곳을 제외하고 외곽만 선으로 이었을 때,
수평선의 시작점과 height가 0인 마지막 포인트 하나로 구성된 Points 그룹을 만드시오.
접근 방법
우선 문제를 이해하는게 중요하다.

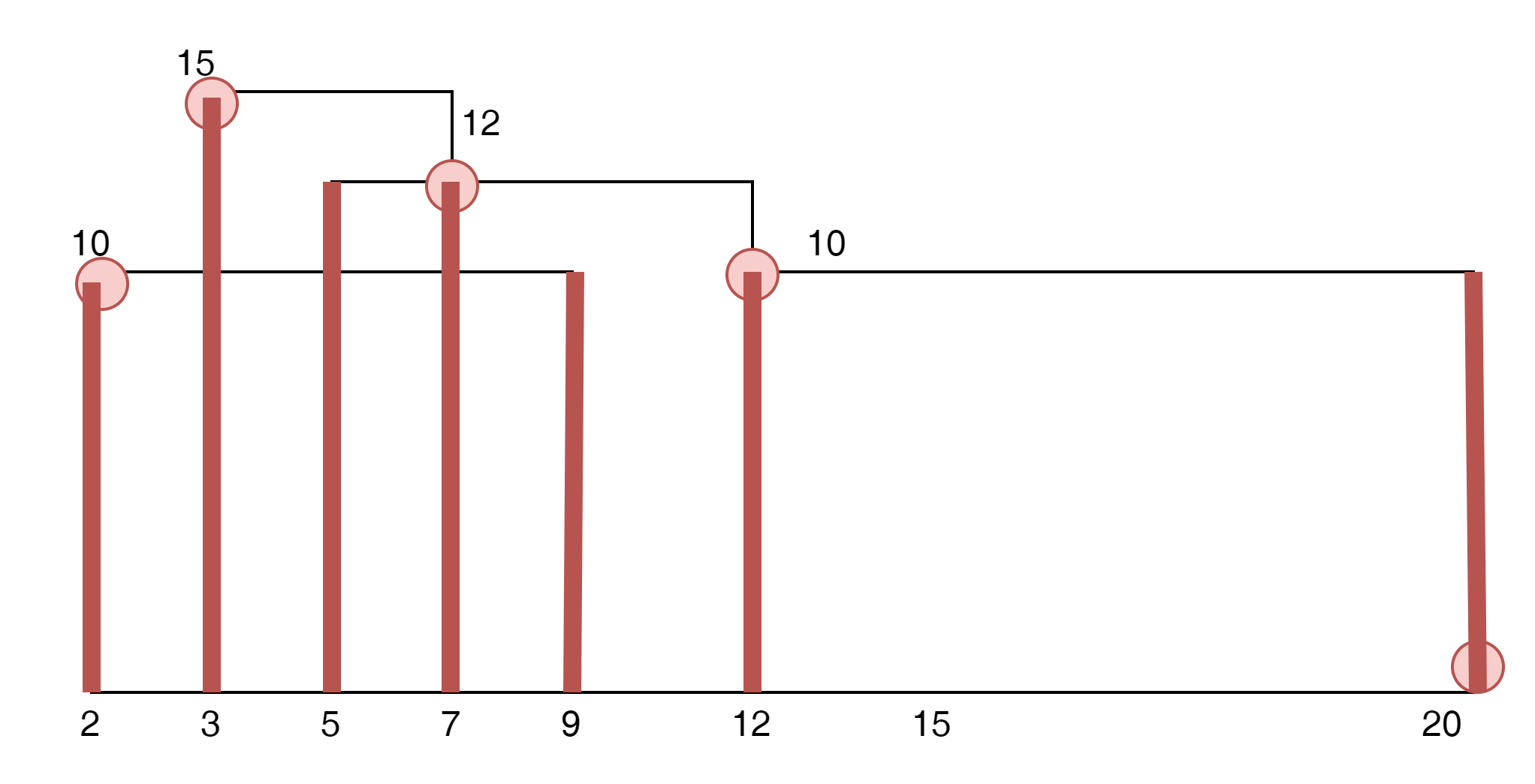
상기와 같은 문제가 주어졌다고 생각해 보자.

답은 outline의 수평선이 시작하는 포인트가 답이 된다.
x와 높이 y 즉 height를 좌표로 한다고 했을 때,
- (2,10)은 수평선을 시작하는 점이다.
- (3,15)는 수평선을 시작하는 점이다.
- 여기서 (5,12) 겹쳐진 네모 안에 있기 때문에 불필요한 포인트이다.
- (7,12)는 수평선을 시작하는 점이다.
- (12,10)은 수평선을 시작하는 점이다.
- (20, 0)은 outline을 종료하는 height가 0인 점이다.
이렇게 답을 구할 수 있다.
높이우선 Priority Queue
상기 그림을 보면 알수있는 법칙이 몇가지 있다.
- x는 정렬되어있다.
- x의 시작포인트와 종료 포인트를 모두 모으면 2에서 부터 20가지의 하나의 직선이 만들어 진다.
예를 들자면 다음과 같다.

모든 수평선을 하나로 합치면

2에서 20까지의 선이 만들어 진다.
이것을 Height가 가장 높은 선부터 계산해 나가게 되면 각 평행선을 구할 수 있게 된다.

우선 가장 높은 선인 (3,7,15) (start, end, height)를 선택한다.
3에서 부터 7까지의 선이 존재하고 높이는 15이다.
다음 높은 선은 (5,12,12) (start, end, height) 가 된다.

그런데 문제점은 start point 5에서 7까지의 선은 이미 점유되고 있다.

앞서 겹친 부분을 제외하고 start 7 에서 12까지 높이 12인 선을 선택한다.

다음은 2에서 3까지를 제외한 나머지라인이 모두 선점 되어있는 상태이다.

2에서 3만 남겨놓고 나머지는 삭제 한다.

마지막으로 12에서 20까지의 start, end point line을 만들고 마지막 x에 존재하는 20과 높이 0을 답으로 정리하면 된다.
상기 접근 방법은 우선순위 큐를 사용해서 height가 가장높은 (start, end, height) point를 뽑고, 하나의 수평 라인을 만들고 답을 뽑아내는 방법을 사용하는데, Time Complexity에서 문제가 생긴다.
우선 Priority Queue를 사용했음으로 Input O(log N), Pop O(1)을 사용하는데 여기까지는 문제 될것이 없다.
2020.09.14 - [Problem Solving] - Javascript Priority Queue 오름 차순
그러나 (start, end point, height)를 하나 뽑을때마다 앞서 답으로 만들어진 평행선과 일일이 비교해야 하는 문제점이 생긴다.
여기서 $ O(N^2) $으로 시간복잡도가 높아지게 된다.
Left to Right Priority Queue
앞서 Priority Queue를 이용해서 문제 접근이 가능하다는 것을 확인했다.
이제 왼쪽에서 오른쪽으로 Point를 순회하면서 문제를 접근 하는 방법을 알아보자.
답이 될 수 있는 Point를 아래 그림과 같이 생각해 보자.
각 붉은 색은 답이 될 수 있는 가능성이있는 선들의 모임이다.
기존에 주어진 문제를 이 가능성이 있는 선들의 모임으로 변경 시켜 보자.
$ [2,9,10],[3,7,15],[5,12,12],[12,20,10],[19,24,8] $
start, end, height로 구성된 input 을 (x point, height, start flag)로 분리 시켜 보겠다.
[2,10,true],[9,10,false],[3,15,true],[7,15,false],[5,12,true],[12,12,false],[12,10,start],[20,10,false],[19,8,true],[24,8,false]
이렇게 분리를 시키고 상기 그림처럼 붉은 선을 위치 시키기 위해서는 x좌표를 기준으로 sorting 처리가 필요하다.
[2,10,true],[3,15,true],[7,15,false],[5,12,true],[9,10,false],[12,12,false],[12,10,start],[19,8,true],[20,10,false],[24,8,false]
그런데 이 sorting 처리에서 고민 해야할 부분이 있다.
만약 동일 x좌표에 포인트가 있다면 무었을 우선처리 해야 할까?
예를 들자면
[12,12,false],[12,10,start]
이 두점이 문제가 된다.
end가 false인 [12,12,false]는 [12,0]이라고 하는 답이 될 가능성이 있다.
그러나 동일 포인트에 start가 위치 한다면 [12,0]은 무시되고, [12,10]이 답이 된다.
즉, 동일 x 포인트에 포인트가 있다면 end보다는 start의 우선순위가 높다는 것을 알 수 있다.
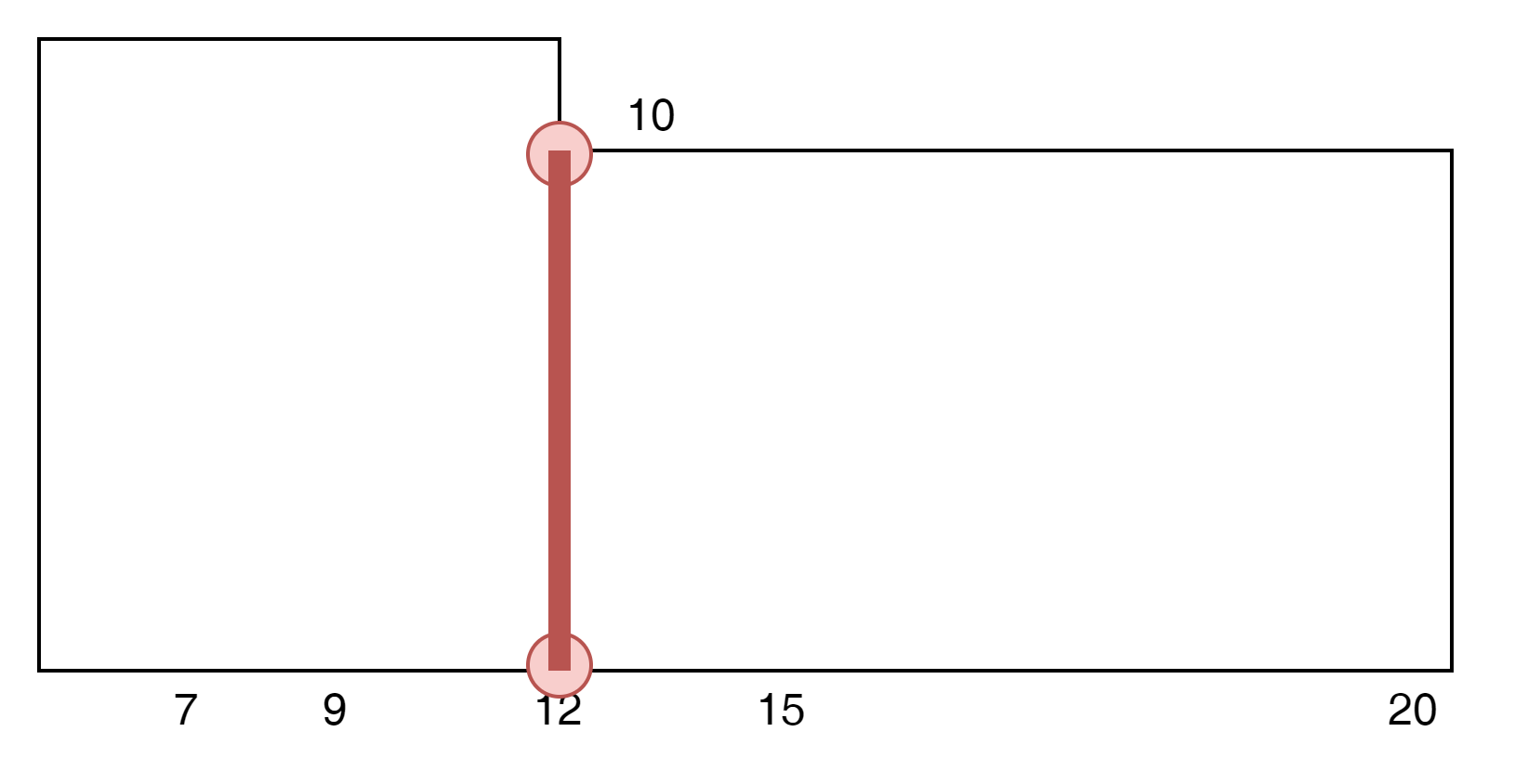
상기 그림 상태에서는 start를 갖고 있는 (12,10)이 답이 되어야 하고 (12,0)은 삭제 되어야 한다.
그럼 동일한 시작점인 경우는 어떻게 되어야 할까?

(15,8)과 (15,10)중 height가 더 높은 10이 더 우선 순위를 갖는다.
단, end 지점의 경우는 오름차순 sorting이 필요한데, 가장 높은 height를 가장 마지막에 삭제 함으로써 height의 변화를 최소화 할 수 있기 때문이다.

상위 그림에서 보면 height 10, 8 이렇게 두개가 있는데
현재 height는 10상태가 된다. 8의 높이를 먼저 삭제하고, 10의 높이를 다음에 삭제하면 최종적으로 8과 10이 삭제 되고 높이는 0만 남게 된다.(이부분은 아래 코드를 봐야 이해가 될 것이다. 그렇지 않으면.. 이해 안될 듯)
이제 sorting의 기준을 다시 정리해 보자.
- x기준으로 sorting한다.
- 동일 x에서는 start가 end보다 우선순위가 높다
- 동일 x에 end라면 height의 높이가 낮은것이 우선순위가 높다.
- 그외 동일 x에서는 height가 높은 point가 우선순위가 높다.
이 기준으로 sorting을 한다면 아래와 같이 코드를 만들 수 있다.
array.sort((a,b)=>{
if(a[0] === b[0] && a[1] === b[1]){ // 양쪽이 같을때
return a[2] ? -1 : 1; //start 우선 end 이후
}
if(a[0] === b[0]){ //x가 같을 때
if(a[2] === b[2] && a[2] === false){//end 일때 height 오름
return a[1] - b[1];
} else if(a[2] !== b[2]){//start end 혼합시
return a[2] ? -1 : 1; //start 우선 end 이후
} else {
return b[1] - a[1]; //그외 height 내림
}
}
return a[0] - b[0]; // x 내림차순
});input이 $ [[1,2,1],[1,2,2],[1,2,3]] $ 일경우
sorting된 결과는
[
[ 1, 3, true ],
[ 1, 2, true ],
[ 1, 1, true ],
[ 2, 3, false ],
[ 2, 2, false ],
[ 2, 1, false ]
]
이렇게 된다.
다시 원래 문제를 풀어보자. 앞서 나온 문제를 포인트 분리해서 sorting시키게 되면 아래와 같이 나오게 된다.
[
[ 2, 10, true ],
[ 3, 15, true ],
[ 5, 12, true ],
[ 7, 15, false ],
[ 9, 10, false ],
[ 12, 12, false ],
[ 12, 10, true ],
[ 19, 8, true ],
[ 20, 10, false ],
[ 24, 8, false ]
]
이 값을 왼쪽에서 부터 오른쪽으로 욺직여 가면서 결과 값을 넣어보자.
왼쪽에서 오른쪽으로 갈때 가장 중요하게 봐야하는 것은 height이다. 꼭 이점을 생각해 보자.

[2,10]은 높이의 변화가 일어났는가?
그렇다 10이라는 최고점이 생겨났다. 답의 대상이라고 생각할 수 있다.

[3,15]는 최고점 변화가 일어났는가? 일어났다. 최고점은 15로 올라갔다. 답의 대상이 된다.

[5,12]는 최고점 변화가 있는가? 아니다 아직 최고점은 15에 존재 한다. 답이 되지 않는다.

[7,15]는 end 지점임으로 15라는 height는 더 이상 존재 하지 않는다. 다음 height는 12로 변경된다. height가 변경되었음으로 답의 대상이 된다.

[9,10]은 end이고 height가 12상태를 유지 함으로 답의 대상이 되지 않는다.

[12,10]을 입력해도 앞선 12의 height가 가장 높음으로 답이 되지 않는다. 그러나

[12,12] false가 앞선 12의 높이를 삭제하고 다음 높이인 앞서 입력한 10이 다음 height가 되면서.
[12,10]은 답의 대상이 되게 된다.
마지막으로

[20,10]을 false로 삭제 함으로써 최종적으로 (20,0)이 되게 된다.
이부분은 Max Heap(Prirority Queue)를 사용하는 파트로써 아래 코드를 보고 이해가 필요하다.
let heap = new MaxHeap();
heap.push(0);
let tmp = new Array();
for(let [x,height,flag] of array){
let max = heap.peek();
if(flag){ //start
heap.push(height);
} else {
heap.delete(height);
}
if(max !== heap.peek()){
tmp.push([x, heap.peek()]);
}
}간단히 코드 설명을 하자면,
heap.push(0);
Max Heap은 가장 높은 값을 우선적으로 빼기 때문에 마지막 포인트에 필요한 0이라는 height값을 미리 입력해 놓는다.
let max = heap.peek();
왼쪽에서 오른쪽으로 Search하면서 현재의 Point의 height를 순차적으로 입력하기 전에
직전 Max값을 미리 저장해 놓는다. 이것은
if(max !== heap.peek()){
tmp.push([x, heap.peek()]);
}
앞서 Point가 입력됨으로써 height에 변화가 있는지를 확인하게 되는데, Height에 변화가 있다는 것은 답이 된다는 의미가 된다.
if(flag){ //start
heap.push(height);
} else {
heap.delete(height);
}
Start Flag 는 새로운 height가 입력되었다는 것을 알려주고, delete는 앞서 입력된 height가 종료되었다는 것을 알려주게 된다.
Time Complexity는 sorting하는데 사용된
$$ O(N Log N) $$
이 된다.
var MaxHeap = (function(){
function MaxHeap(){
this.heap = new Array(1).fill(0);
};
MaxHeap.prototype.push = function(height){
this.heap.push(height);
let position = this.heap.length - 1;
while(1 < position){
let parent = Math.floor(position/2);
if(this.heap[parent] < this.heap[position]){ //switch position
this.swap(position, parent);
position = parent;
} else {
break;
}
}
};
MaxHeap.prototype.pop = function(){
if(this.heap.length === 1) return undefined;
if(this.heap.length === 2) return this.heap.pop();
let result = this.heap[1];
this.heap[1] = this.heap.pop();
let position = 1;
this.downHeap(position);
return result;
};
MaxHeap.prototype.swap = function(left, right) {
let temp = this.heap[right];
this.heap[right] = this.heap[left];
this.heap[left] = temp;
};
MaxHeap.prototype.peek = function() {
return this.heap[1];
};
MaxHeap.prototype.delete = function(height) {
for (let i = 1; i < this.heap.length; i++) {
if(this.heap[i] === height){
this.remove(i);
break;
}
}
};
MaxHeap.prototype.downHeap = function(position){
while (position * 2 < this.heap.length) {
let left = position * 2;
let right = position * 2 + 1;
if(right < this.heap.length && this.heap[position] < this.heap[right] && this.heap[left] < this.heap[right]){ // right가 존재하고 right가 position 및 left보다 클 경우
//position right swap
this.swap(position, right);
position = right;
continue;
}
if(right < this.heap.length && this.heap[position] < this.heap[left] && this.heap[right] < this.heap[left]){ // right가 존재하고 left가 position 및 right보다 클경우
//position left swap
this.swap(position, left);
position = left;
continue;
}
if(this.heap[position] < this.heap[left]){ // left가 position보다 클경우
//position left swap
this.swap(position, left);
position = left
} else {
break;
}
}
};
MaxHeap.prototype.remove = function(position){
if(position + 1 === this.heap.length) {
this.heap.pop();
return;
}
this.heap[position] = this.heap.pop();
this.downHeap(position);
return;
};
return MaxHeap;
}());
var getSkyline = function(buildings) {
let array = new Array();
for (let i = 0; i < buildings.length; i++) {
array.push([buildings[i][0],buildings[i][2], true]) //start
array.push([buildings[i][1],buildings[i][2], false]) //end
}
array.sort((a,b)=>{
if(a[0] === b[0] && a[1] === b[1]){ // 양쪽이 같을때
return a[2] ? -1 : 1; //start 우선 end 이후
}
if(a[0] === b[0]){ //x가 같을 때
if(a[2] === b[2] && a[2] === false){//end 일때 height 오름
return a[1] - b[1];
} else if(a[2] !== b[2]){//start가 우선
return a[2] ? -1 : 1; //start 우선 end 이후
} else {
return b[1] - a[1]; //그외 height 내림
}
}
return a[0] - b[0]; // else
});
let heap = new MaxHeap();
heap.push(0);
let tmp = new Array();
for(let [x,height,flag] of array){
let max = heap.peek();
// console.log(heap.heap);
if(flag){ //start
heap.push(height);
} else {
heap.delete(height);
}
if(max !== heap.peek()){
tmp.push([x, heap.peek()]);
}
}
return tmp;
};마지막으로 Merge Sorting을 이용한 방법이 있는데, 시간을 너무 많이 써서 다음에 추가적으로 작성 하겠다.
'Problem Solving' 카테고리의 다른 글
| Edit Distance (Levenshtein 알고리즘) (0) | 2021.07.07 |
|---|---|
| One Edit Distance (0) | 2021.07.05 |
| Max Points on a Line (0) | 2021.06.27 |
| Greatest common divisor (gcd) 최대 공약수 구하기, Euclidean algorithm 유클리드 알고리즘 (0) | 2021.06.27 |
| Reaching Points (0) | 2021.06.26 |
