문제 내용
두개의 word가 주어 진다.
예) 'abc', 'abd'
다음 3개준 하나의 Operation이 가능하다고 할때
- delete : char 하나를 삭제한다
- input : char 하나를 넣는다.
- replace : char 하나를 바꾼다.
두개의 word가 같아 질 수 있도록 최소한의 Operation 횟수를 구하라.
접근 방법
처음에는 이와 비슷한 문제인
2021.07.05 - [Problem Solving] - One Edit Distance
를 사용해서 Two Points를 이용한 해결 방법을 모색하였다.
그러나 최종적으로 이와 같은 접근법으로는 해결 할 수없다는 것을 알 수 있었다.
본 문제는 Levenshtein 알고리즘을 알고 있느냐에 따라서 쉽게 문제를 해결하거나 또는 해결하기 굉장히 어렵게 될 것이다.
자세한 풀이 방법은 위를 참조 하면 되지만, 나름 해당 알고리즘의 접근 방법을 다음과 같이 풀이 하고자 한다.
우선 문제의 접근을 줄여가면서 가능한가를 생각해 보자.
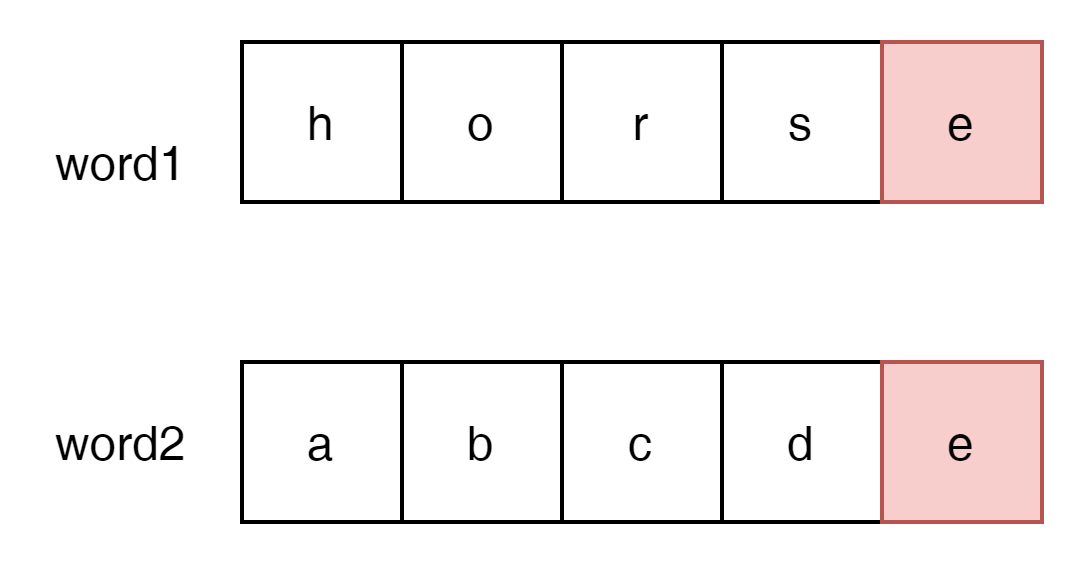
'horse'와 'abcde'라는 두개의 words를 비교해 보자. 마지막 'e' 는 동일한 값이다. 해당 문제는 다음과 같이 줄여서 생각할 수 있게 된다.

그럼 's'와 'd'는 어떠한가?
서로 다른 값이 되어있다. 둘중에 하나의 값을 replace함으로써 문제해결이 가능하다.

대신에 한번의 Operation이 일어났음을 확인 할 수있다.
같은 방법으로 다음과 같이 문제가 주어 졌다면 어떤가?

상기 문제에서는 r 하나만 삭제 한다면, a와 b는 동일 값임으로 Operation 1로써 두개의 words가 동일하게 된다.
즉, 큰 문제를 작은 문제로 잘라가면서 표현 할 수 있다는 것이다.
이것을 순차적으로 접근해 보자.

상기와 같이 문제가 주어졌다고 생각해 보자.
word1은 'horse', word2는 '' 아무값도 없이 주어졌다.
일견에도 5라는 결과 값을 유추 할 수있다.
하지만 문제를 잘라가면서 접근해 보자.
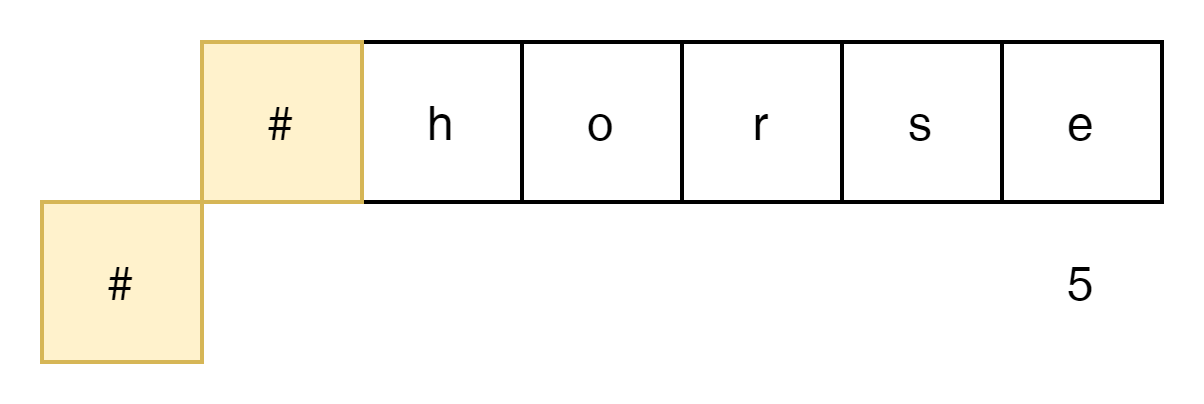
#은 아무것도 없다는 것을 의미한다.
'horse'는 5번의 변화를 통해서 답을 만들어 낼 수 있다.
그럼 'hors'는?

4번, 그리고 hor는 3번 ho는 2번 h는 한번 최종적으로 양쪽다 없는 경우는 0번의 변화로 두 words를 동일하게 만들 수 있다.
그럼 'r'과 'horse'를 비교해 보자.

어떻게 이 값이 가능 한지는 찬찬히 따져봐야 한다.
- 'r'과 'h'가 문제라고 하면 1번의 operation이면 같아질 수 있다.

- 'r'과 'ho'는 2번의 operation이 필요하다.
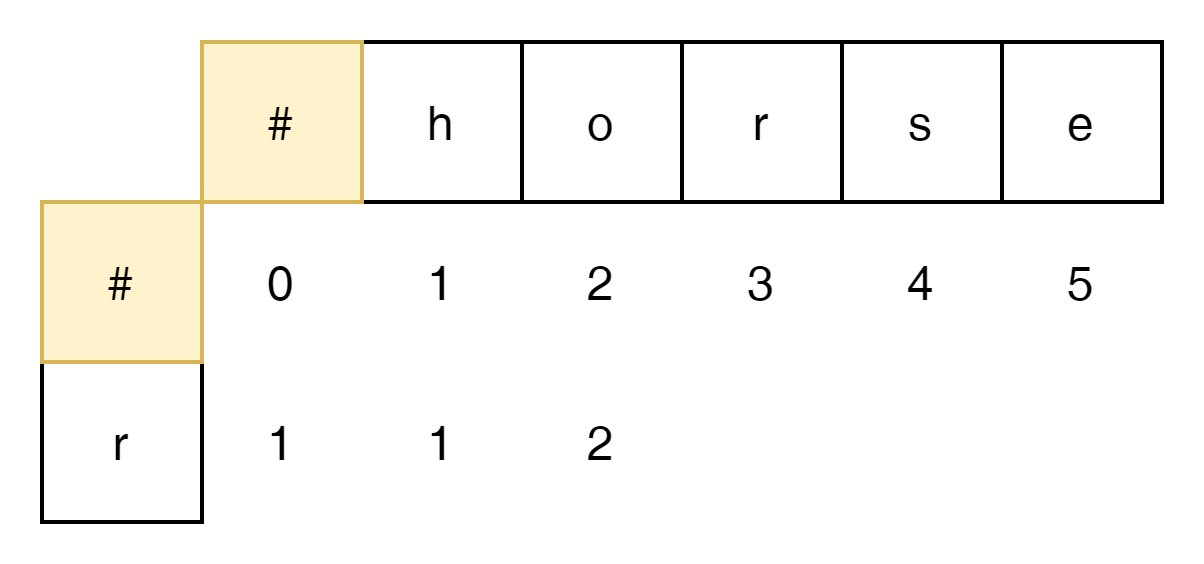
- 'r'과 'hor'은 마지막 r이 동일 함으로 앞선 'h'와 'o'만 삭제되면 된다. 답은 2

- s는 중간에 'r'을 제외 하고 'h','o','s'가 삭제 되면 됨으로 3

그리고 'se'가 추가 되면 r과 연관이 없음으로 3과 4의 Operation이 생겨난다.
이제 'o'를 word2에 하나더 추가해 보겠다.

- 'ro'와 'h'가 같은 값이 되려면 2번의 Operation이 필요하다.

- 'ro'와 'ho'가 같으려면 1번의 Operation이 필요하다.
그럼 'ro'와 'hor'은?

- 'hor' 중 'o'를 제외하고 2번의 Operation이면 가능하다.

최종적으로 'ro'와 'horse'의 차이는 상위와 같다.
여기에 word2에 's'를 하나더 넣어보자.
'ros'와 'horse'의 비교를 진행해 보자.
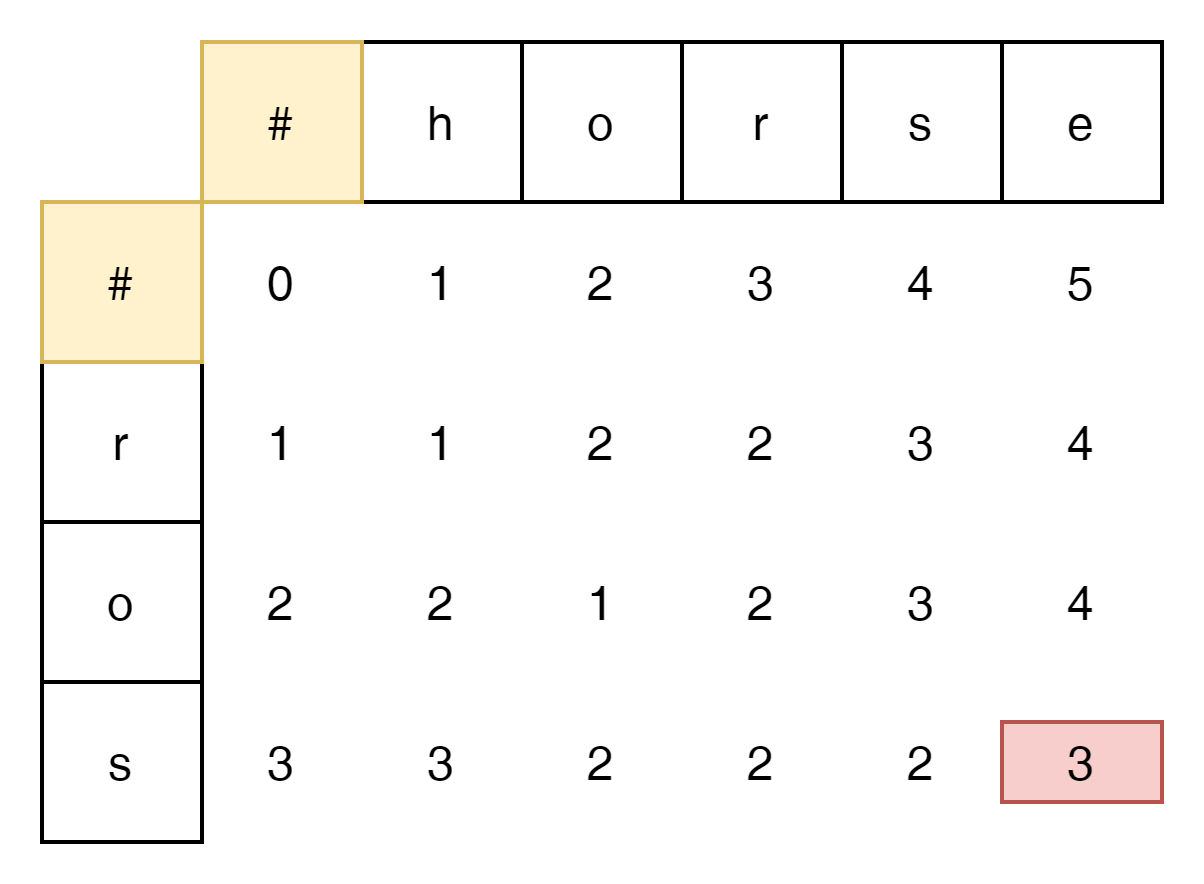
최종적으로 'ros'와 'horse'의 비교값은 '3'이 된다는 것을 알 수 있다.
그럼 위의 표에서 수식을 추측해 보자.
추측의 가장 기본이 되는것은 word1의 char와 word2의 char가 같을 때와 다를때를 기준으로 진행해 보자.
예를 들자면

's'와 'e'는 동일한 값이 아니다.
- 결과 값 3은 주변 3개의 cell중 가장 작은 값의 Plus 1이다.

's'와 'r'은 동일 값이 아니다.
- 결과 값은 주변 3개의 cell중 가장 작은 값 1 plus 1이다.
다른 값들은 어떤거 확인해 보자.
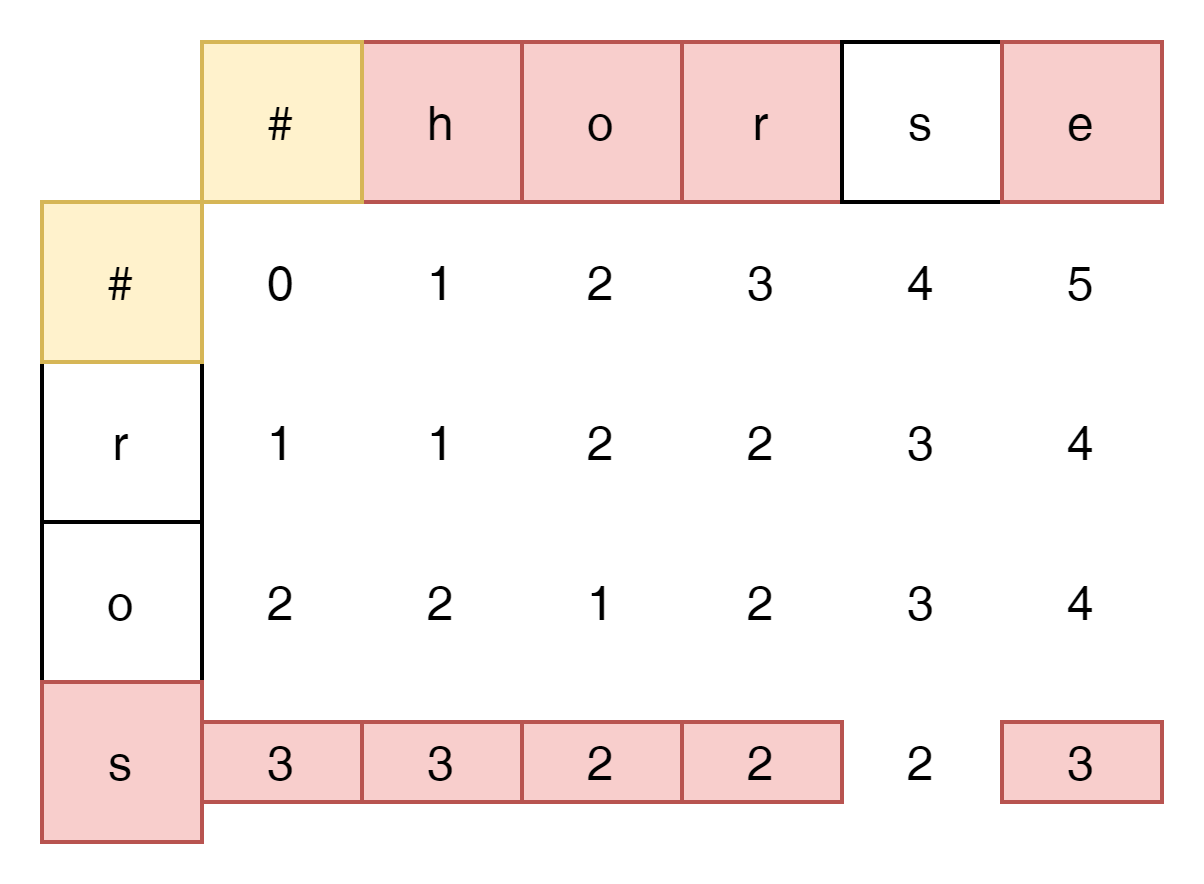
모든 불일치 pair의 주변 3개의 cell중 가장 작은 값의 +1이라는 규칙을 갖는다.
계속해서 다른 쪽 cell을 확인해 보자.
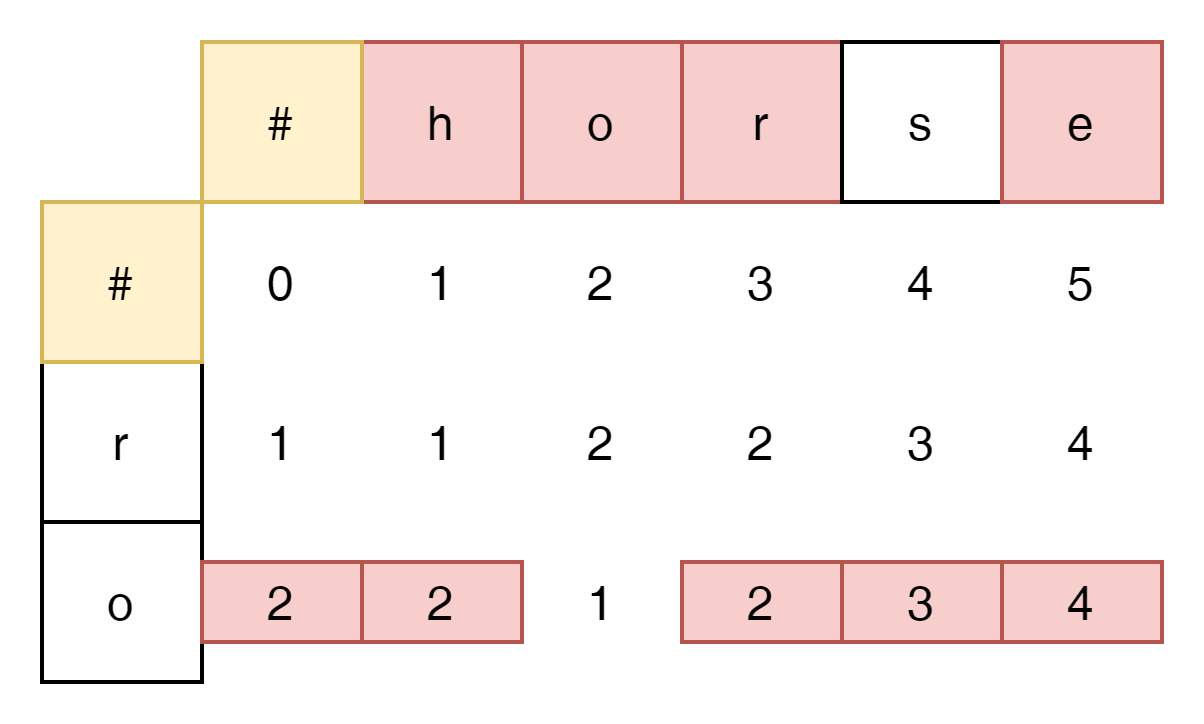
'o'역시 마찬가지다.
모든 결과를 비교해보면 다음과 같은 규칙이 성립됨을 확인 할 수 있다.
- if word1 char !== word2 char then
- Math.min(dp[wordchar1-1][wordchar2], dp[wordchar1][wordchar2-1],dp[wordchar1-1,wordchar-2])+1

위 그림에서 파란색이 min function안에 존재하는 값이라고 생각하면 된다.
이제 같은 값일때만 추가적으로 확인하면 된다.
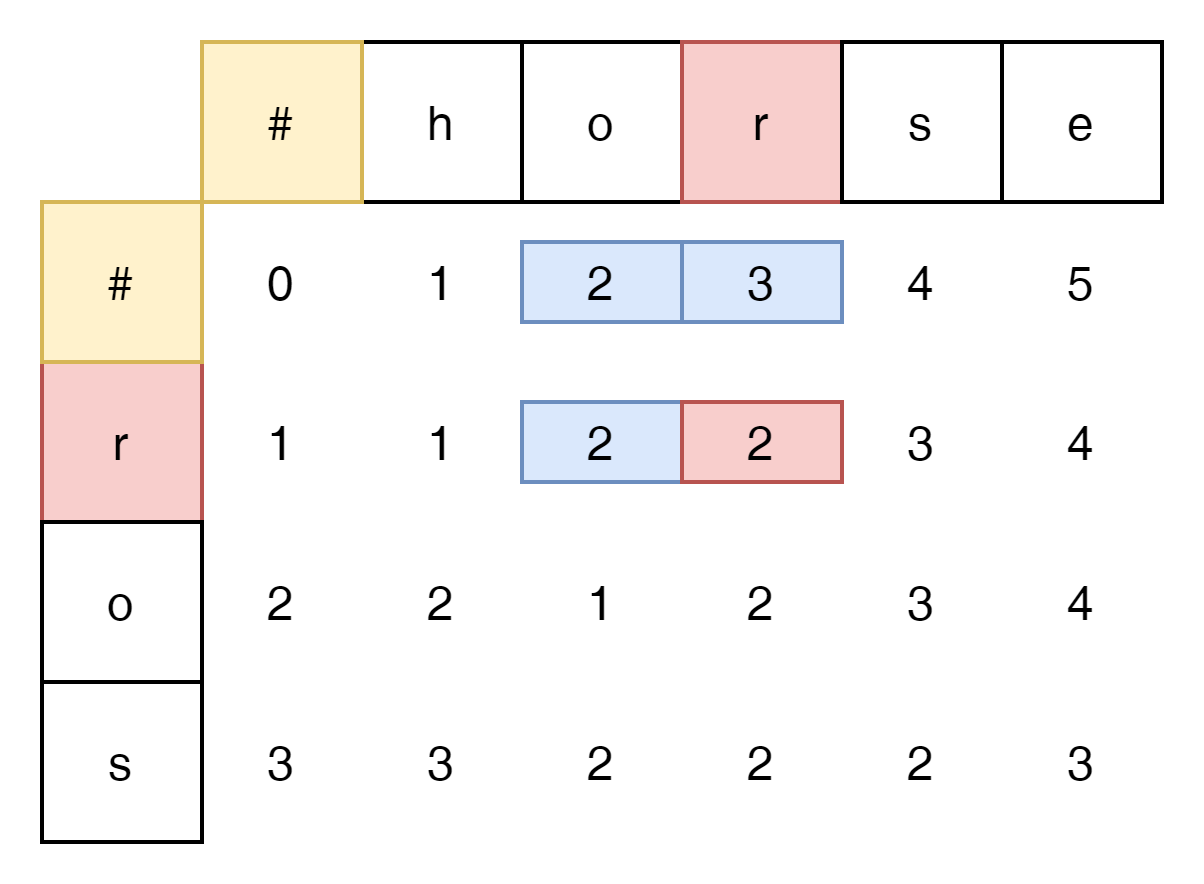
r이 같을때 주변의 3개 cells중 가장 낮은 값과 같다.
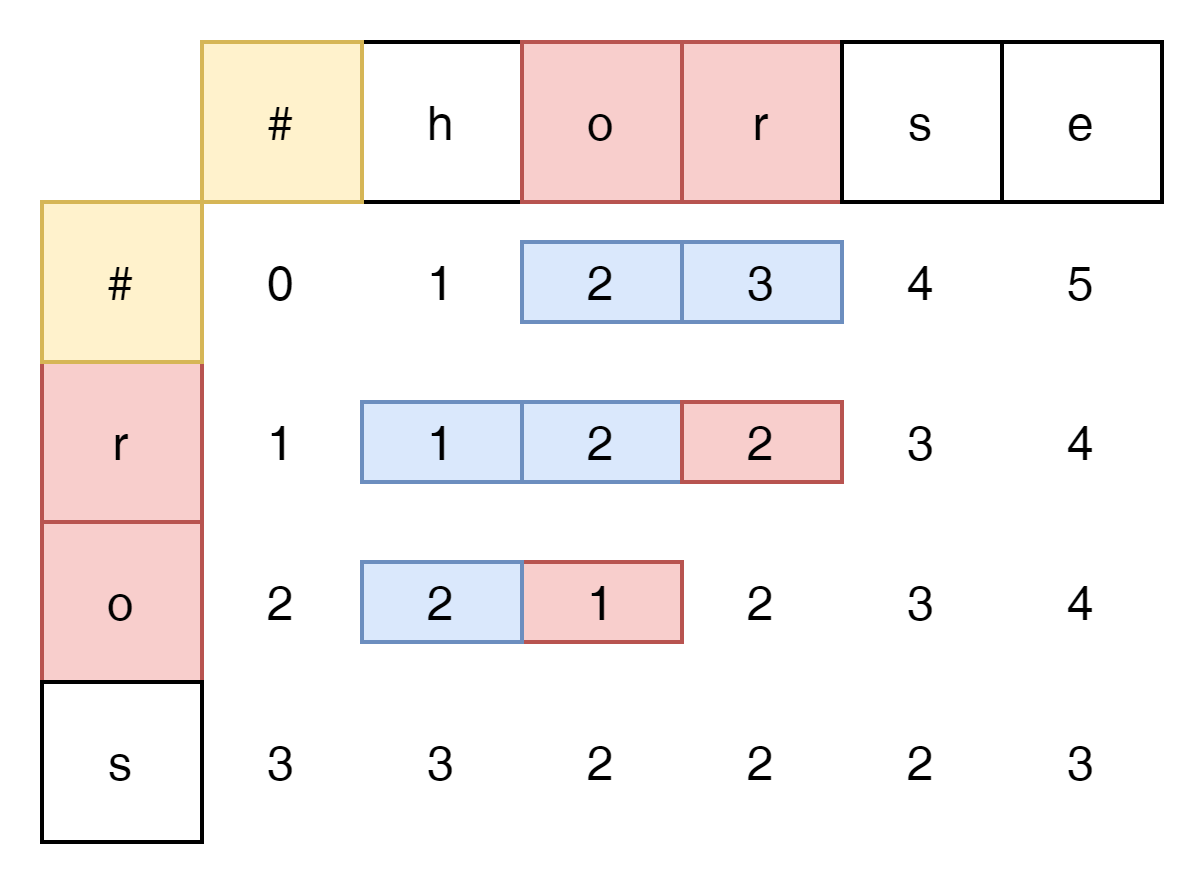
o역시 가장 작은 값과 같다.
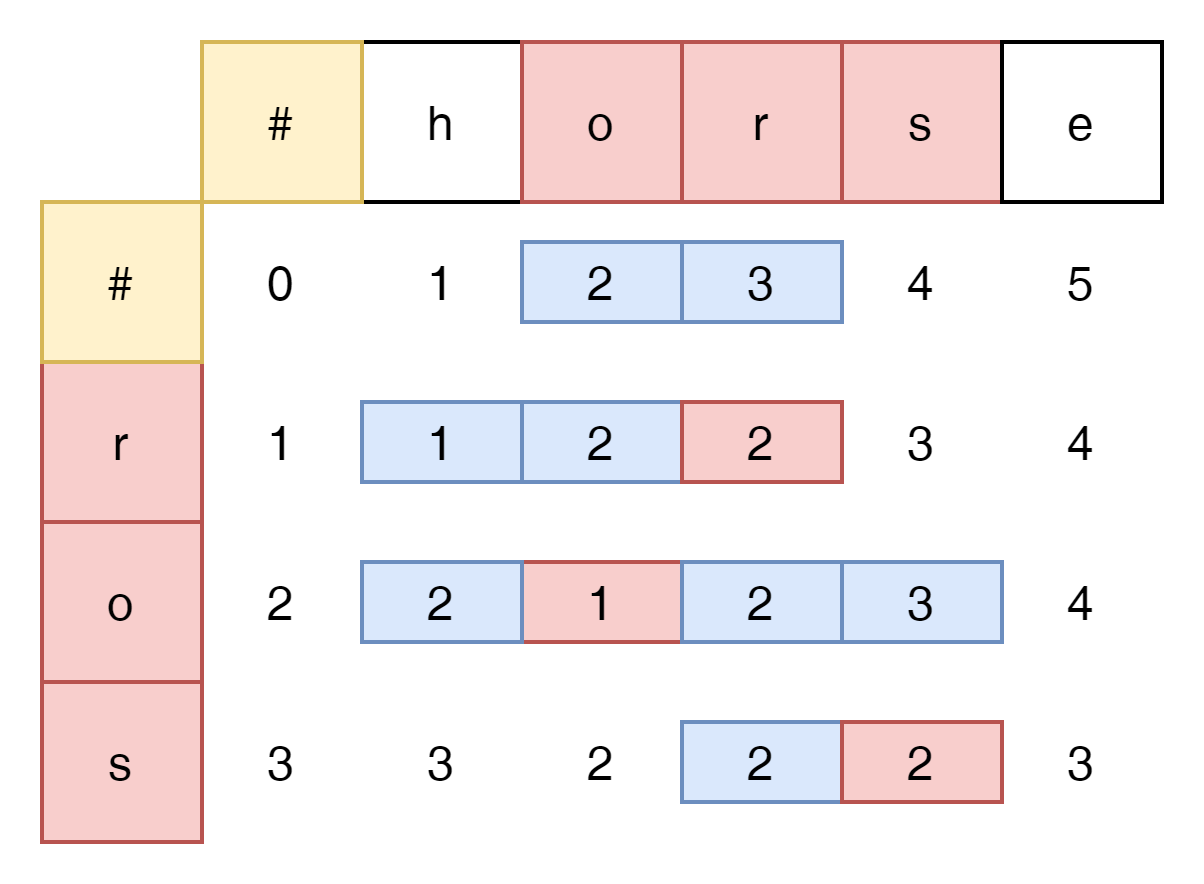
s역시 가장 작은 값과 같다.
다음과 같은 식이 만족 될 수 있다.
- if word1 char === word2 char then
- Math.min(dp[wordchar1-1][wordchar2], dp[wordchar1][wordchar2-1],dp[wordchar1-1,wordchar-2])
그러나 불행히도 예외가 발생하는 경우가 있다.
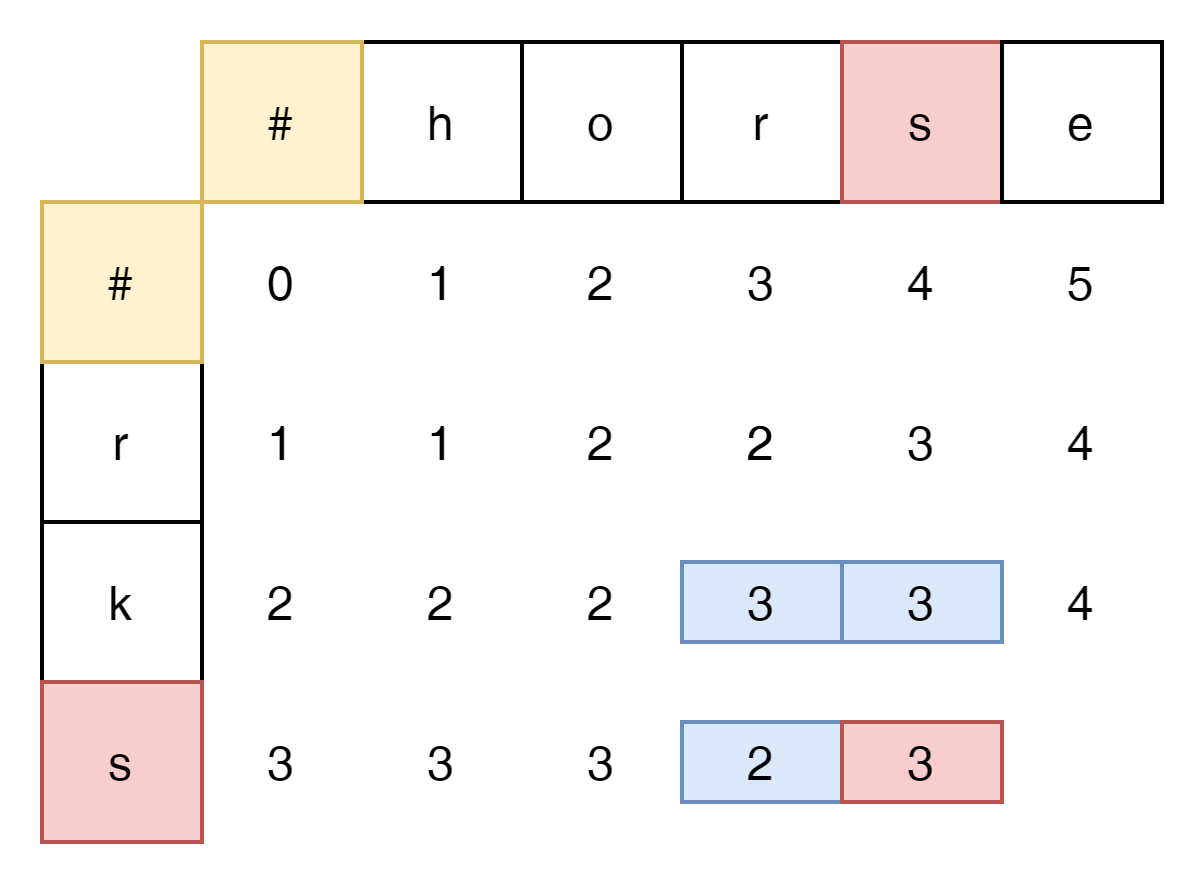
대각선의 값이 최소값이 아닌 경우는 최소값 +1이 답이 되는 상황이다.
이와 같은 경우를 회피 하기 위해 다음과 같이 식을 변경해야 한다.
- if word1 char === word2 char then
- Math.min(dp[wordchar1-1][wordchar2], dp[wordchar1][wordchar2-1],dp[wordchar1-1,wordchar-2]-1) + 1
즉 대각선 cell의 값이 최소값인 경우만 앞선 값을 copy해오고 그외의 값은 +1이 필요하다.
사실 이 부분을 본 알고리즘을 모른 상태에서 과연 추측해 낼 수 있을까?
개인적으로는 불가능해 보인다. 이 알고리즘을 미리 알지 못한다면 시간내에 문제를 풀긴 쉽지 않을 것이다.
그러나 단어의 유사도를 찾는 알고리즘으로 굉장히 잘 알려진 내용이기 때문에 이번 기회에 잘 기억 해 놔야 할 것 같다.
Time Complexity는
$$ O(nm) $$
이다.
var minDistance = function(word1, word2) {
let arr = new Array(word1.length + 1).fill(0).map(_=> new Array(word2.length + 1).fill(0));
for(let row = 0; row < arr.length; row++){
arr[row][0] = row;
}
for(let col = 0; col < arr[0].length; col++){
arr[0][col] = col;
}
for(let row = 1; row < arr.length; row++){
for(let col = 1; col < arr[0].length; col++){
if(word2.charAt(col-1) !== word1.charAt(row-1)){
arr[row][col] = 1 + Math.min(arr[row-1][col],arr[row][col-1],arr[row-1][col-1]);
} else {
arr[row][col] = 1 + Math.min(arr[row-1][col],arr[row][col-1],arr[row-1][col-1] -1);
}
}
}
// console.log(arr);
return arr[word1.length][word2.length];
};
'Problem Solving' 카테고리의 다른 글
| Average Selling Price (0) | 2021.07.20 |
|---|---|
| Find Center of Star Graph (0) | 2021.07.14 |
| One Edit Distance (0) | 2021.07.05 |
| The Skyline Problem (0) | 2021.06.30 |
| Max Points on a Line (0) | 2021.06.27 |
