Count of Smaller Numbers After Self
문제 내용
숫자로 이루어진 Array가 주어지고, 각 숫자의 오른쪽에 위치한 숫자중에 현재의 숫자보다 작은 숫자의 갯수를 맞추는 문제 이다.
접근방법
굉장히 다양한 접근이 가능한 문제이다.
가능하다면 모든 경우의 문제를 푸는 것이 좋다고 생각한다.
- full search
- segment tree & binary indexed tree
- insertion sort
- merge sort
full search
모든 경우의 수를 조회하는 방법이다.
예를 들어 보자.

$ [5,2,6,1] $ 이 있다고 생각해 보자.
5보다 작은 우측의 수는
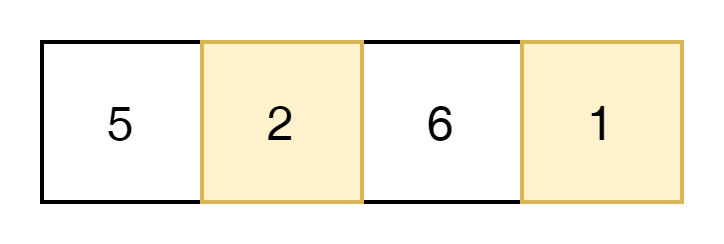
2와 1 두개가 있다.
이것을 알기 위해서는 2,6,1을 한번씩 순회하면 된다.
다음은 2일때다.
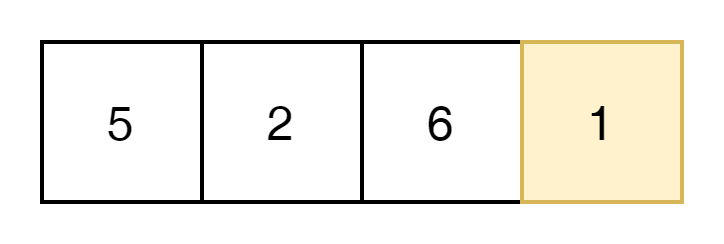
2일때는 6과 1 한번씩 순회 하면 된다.
다시 6일때는 1한번만 더 순회하면 된다.
Time complexity를 보면 N번을 순환 했고 각 경우의 수마다.
$ (n-1) + (n-2) + (n-3) + 1 $ 회를 순환한다.
즉, $ n(n-1)/2 $ 가 되고 $ O(N^2) $이 되게 된다.
그럼 이것을 자료구조를 통해서 최적화 해보겠다.
Segment Tree & Binary Indexed Tree

Search의 방향을 오른쪽에서 왼쪽으로 검색한다고 생각을 해보면,
1,6,2,5의 순서대로 조회가 가능하다.
이때 1,6,2,5를 index로 미리 관리를 하게 된다면 어떨까?

왼쪽은 문제 오른쪽은 index sum이라고 명명하겠다.
index sum은 문제의 value가 나온 횟수를 저장한다고 생각하면 된다.


6이 되었을 때를 생각해 보자. 6이라는 index에 1을 넣기전에 1은 이미 index sum에 위치를 하고 있다.
즉, 6일때 0부터 5까지의 Count Sum을 계산한다면 답이 된다.
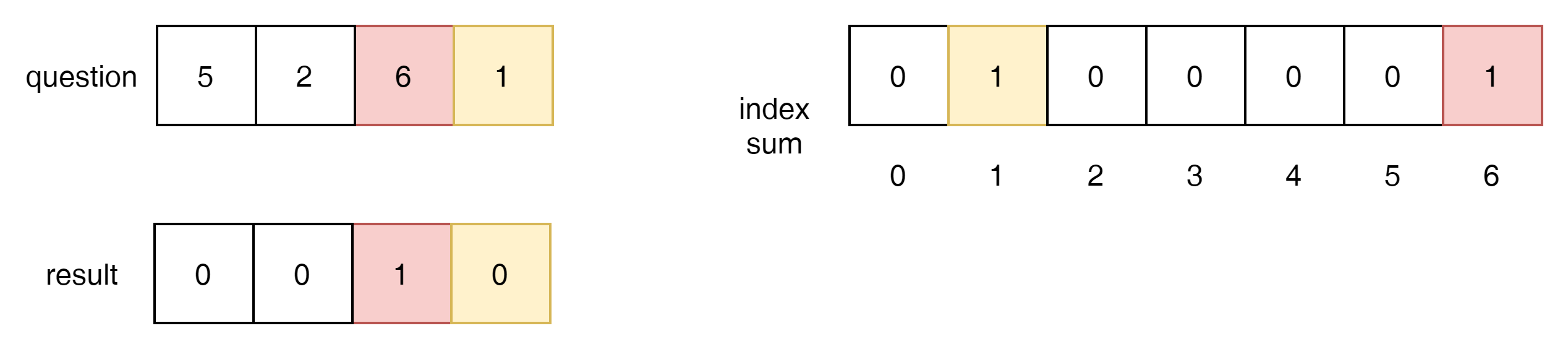
위와 같이 6이 되었을때 result는 1의 count 1이 답이 된다.

2가 왔을때의 index sum range는 0 ~ 2-1 이 된다.

최종적으로 5가 왔을때는 0에서 부터 4까지의 Count를 sum한 2가 답이된다.
이러한 방식을 Time Complexity로 보게 된다면 어쩌면 full search보다 더 높은 복잡도가 나올 수도 있다
가령 $ [0,1000, 1] $ 일 경우 index sum을 위해서 굉장히 많은 양의 array를 만들어야 한다.
물론 count를 세기 위해서 999번 index를 왼쪽에서 오른쪽으로 이동 해야한다.
이점을 개선하기 위해서 Segment Tree와 Binary indexed Tree를 사용하게 되면 $ O(log_2_N) $의 속도로 index sum count가 가능하고 최종적으로는 $ O(N * log_2_N) $ 이 가능하게 된다.
이것이 상기 2가지 자료구조가 binary 구조를 따르기 때문이다.
자세한 것은 다음 내용을 읽어 보기 바란다.
2021.05.02 - [Problem Solving] - Binary Indexed Tree (Fenwick tree)
2021.05.02 - [Problem Solving] - Segment Tree
그럼 다른 방법은 없을까?
Insertion sort
앞서 문제를 오른쪽에서 왼쪽으로 이동하면서 index sum을 count 한다고 했는데, 이것을 응용해서 Insertion sort를 해보도록 하겠다.

$ [5,2,6,1] $이 주어졌다.
1의 오른쪽은 아무것도 없음으로 result 값은 0이 된다.

6의 오른쪽에는 1이 있다. 이것은 명확함으로 result의 값은 1이 추가된다.

그럼 2의 경우는 어디에 위치 해야할까?
2는 6보다 작은 수이다. 그럼 2를 insertion sorting해보자.
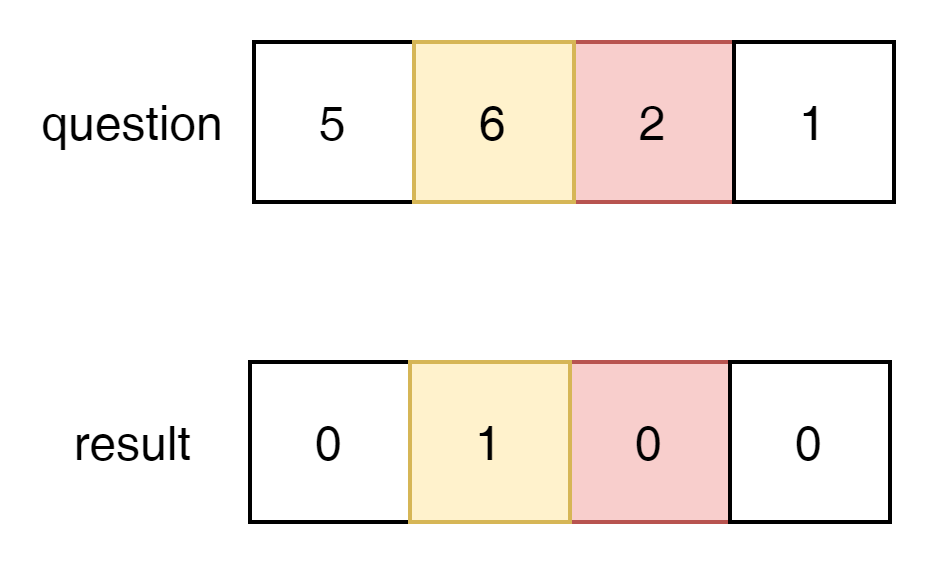
6과 2의 자리를 변경하고 1보단 큼으로 멈추었다.
2는 오른쪽 자리의 length가 자기 자신보다 확실히 작다고 볼수 있음으로 결과 값으로 end index - 자신이 들어간 index로 답을 만들면 된다.

다음은 5이다.
5는 6보다 작음으로 자리를 변경한다.

5는 2보다 큼으로 더이상 자리를 변동시킬 필요없다.
결과 값은 end index 3 - cur index 1인 2가 답이 된다.
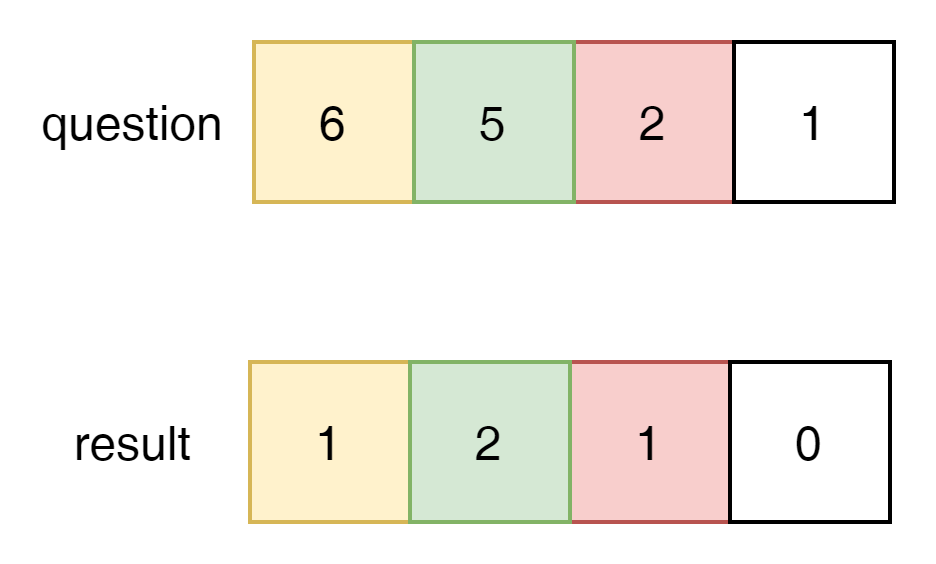
최초 순서에 맞추어서 Result를 정렬하면
$ [2,1,1,0] $ 으로 정답이 된다.
Insertion Sort가 fullsearch보다는 빠를 가능성이 높긴 하지만 근본적으로
Insersion Sort는 $ O(N^2) $ 임으로 적절치 한다.
var countSmaller = function (nums) {
let result = new Array(nums.length).fill(0);
let sorted = new Array();
let dp = new Array();
sorted.push(nums[nums.length - 1]);
dp.push(0);
for (let i = nums.length - 2; 0 <= i; i--) {
let insertIdx = binarySearchLower(nums[i],sorted);
sorted.splice(insertIdx, 0, nums[i]);
dp.splice(insertIdx, 0, 0);
dp[insertIdx] = dp.length - insertIdx - 1;
result[i] = dp[insertIdx];
}
return result;
function binarySearchLower(target,sorted) {
let left = 0;
let right = sorted.length; //lower bound
while (left < right) {
let median = left + Math.floor((right - left) / 2);
if (target > sorted[median]) {
right = median;
} else {
left = median + 1;
}
}
return left;
}
};
Insertion sort가 가능한것을 알았으니, 위에서 착안한 아이디어를 $ O(N log_2_N) $ 인 Merge Sort에 대입해 보겠다.
Merge sort
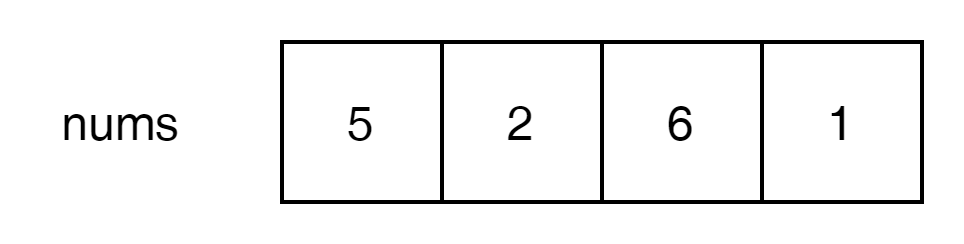
위와 같은 문제가 주어졌다.
merge sort의 기본은 분리하고 다시 합치는 것이다.
우선 분리를 해보도록 하겠다.

이제 다시 합치는 것을 생각해 보자.
우선 5와 2를 보겠다.
2는 5보다 작다 5와 2를 sorting하면

5가 더 큼으로 5를 자리하게 된다. 5는 아직 넘어오지 않은 모든 우측 값보다 더 큰게 확실함으로 우측 section인 2가 있는 length의 갯수만큼 더 크게 된다.

다음 수 2는 아무런 result를 가지 못한다.

같은 방법으로 다음 것을 merge 해보겠다.

그럼 이제 2번째 merge를 진행해 보겠다.

가장 큰 값인 6을 가장 좌측에 자리 잡게 한다.
그러나 6은 우측 section에서 왔기때문에 좌측 Section에서 온값을 result값이 추가 할 수는 없다.
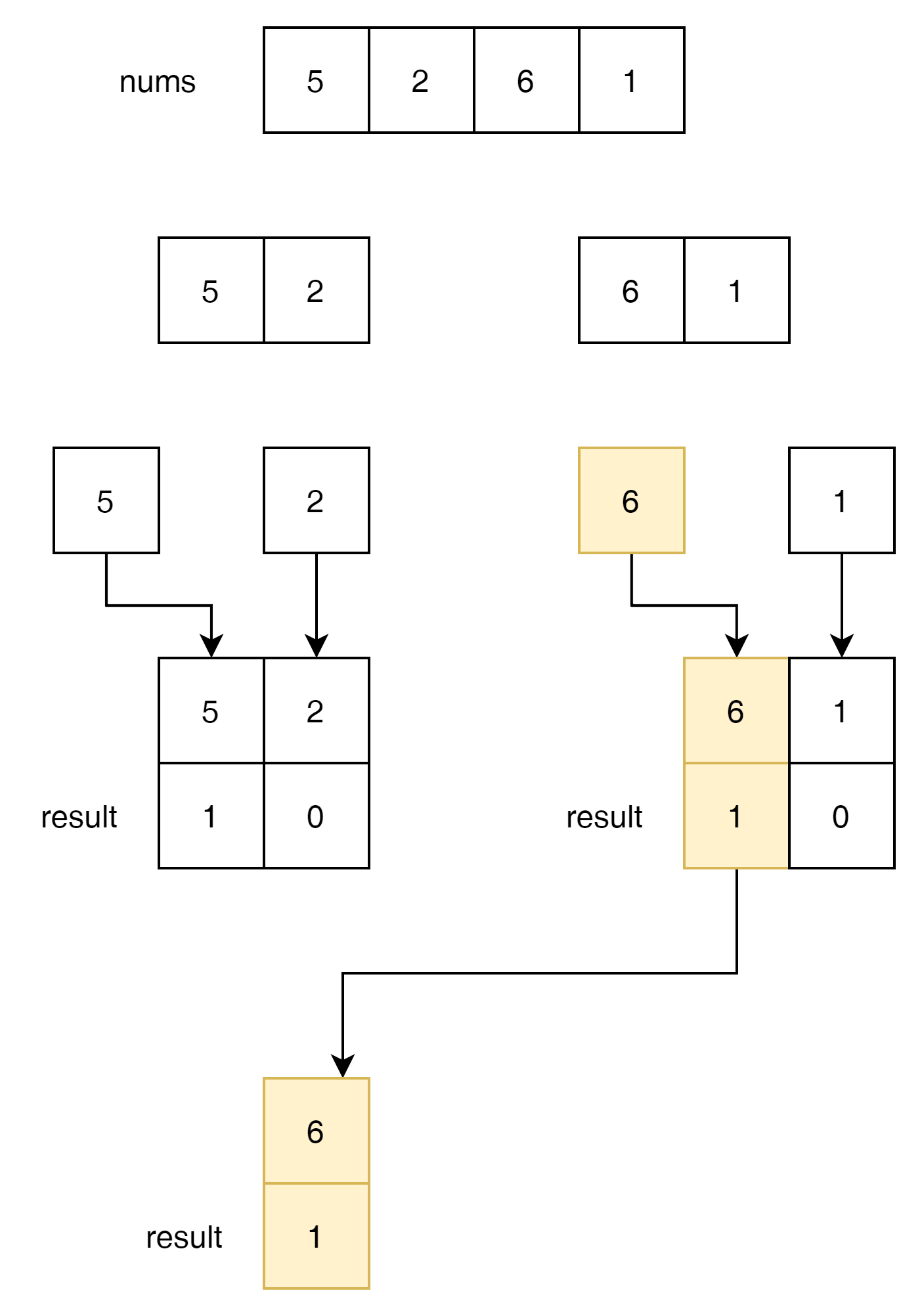
다음 값은 5가 된다.

그런데 5의 경우는 Section 왼쪽에서 왔음으로 오른쪽에서 merge가 진행이 될 나머지 값이 있다면 이 값을 결과 값에 추가 해도 문제가 없게 된다.
지금은 우측에 1이 하나 남아 있음으로 현재 result 1 + 1을 더해서 2가 되게 된다.
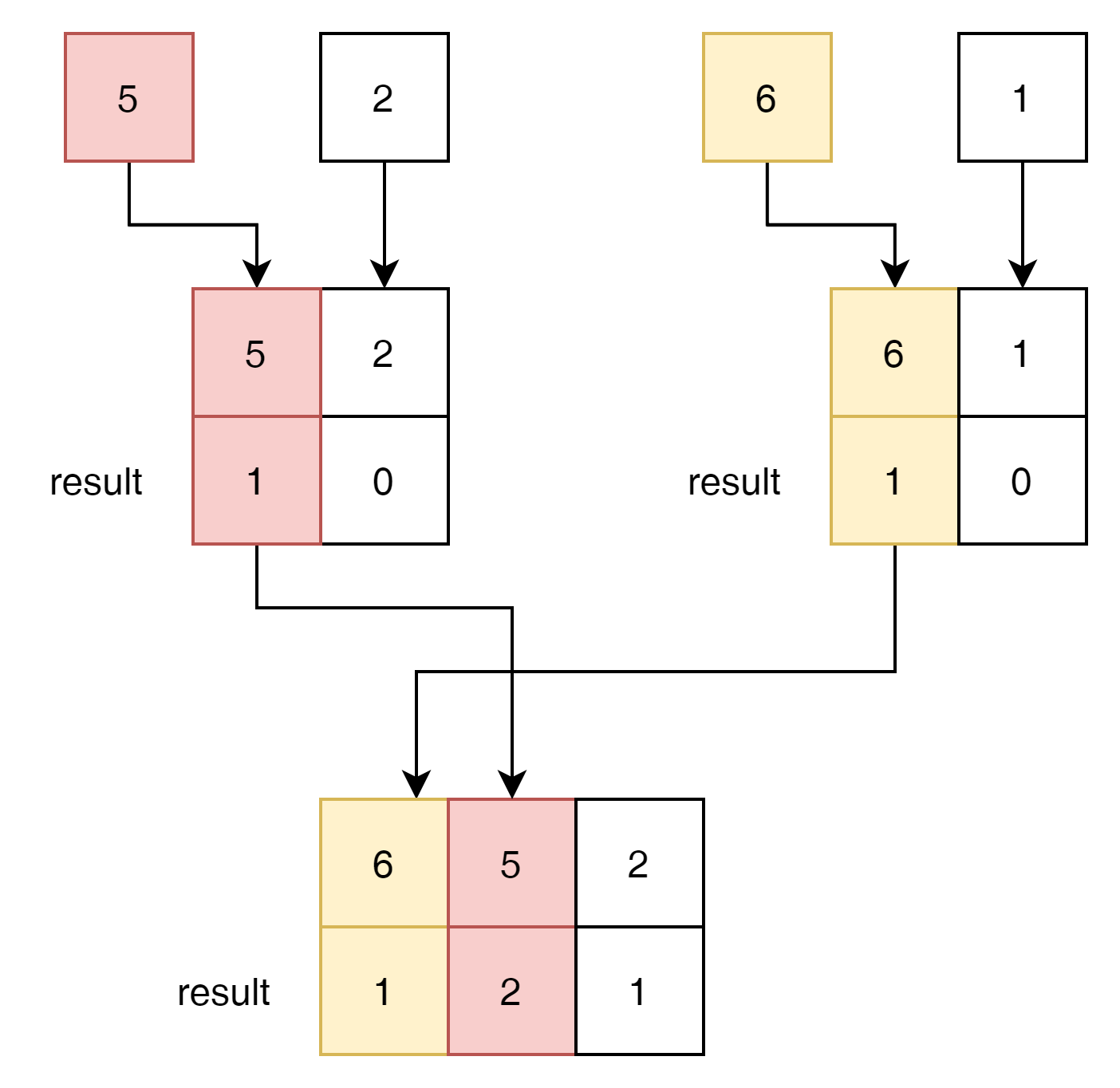
다음 2역시 우측 section에 1이 아직 남아있음으로 현재 result 0 + 우측에 남아있는 length 1을 더해서 1 result가 1이 된다.

최종적으로 result는 $ [1,2,1,0] $ 이 되게 되고 이것을 index 순서로 맞추면
$ [2,1,1,0] $이 답이 되게 된다.
주어진 문제 array nums와 result에 대한 변화를 주지 않기위해서 프로그램기술로 중간에 indices라고 하는 Proxy용 Array을 운영 할 수 있다.


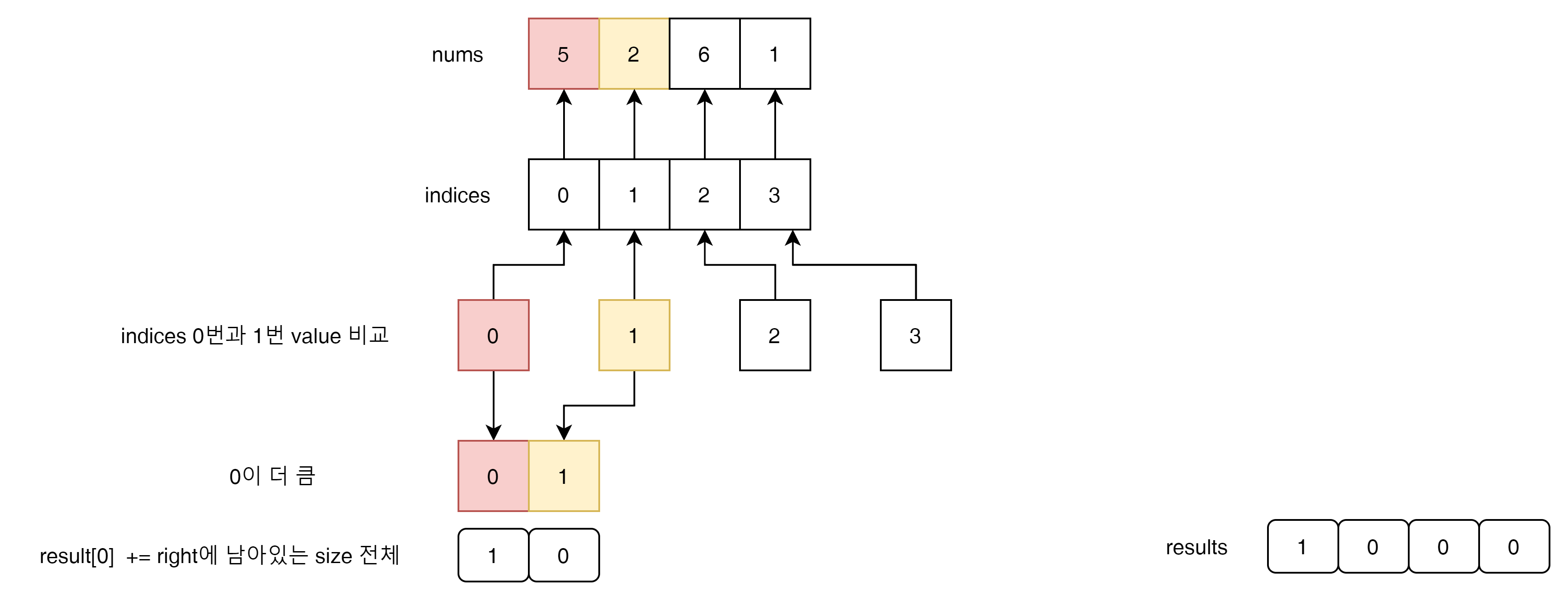
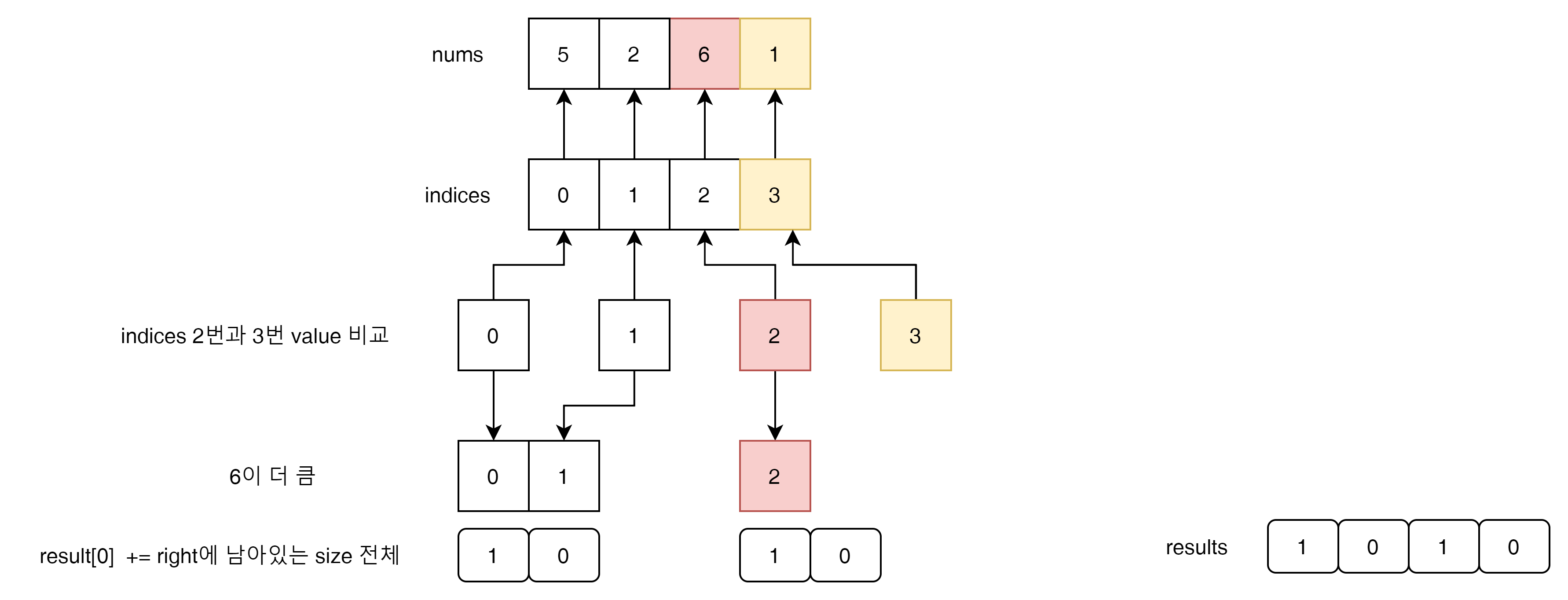

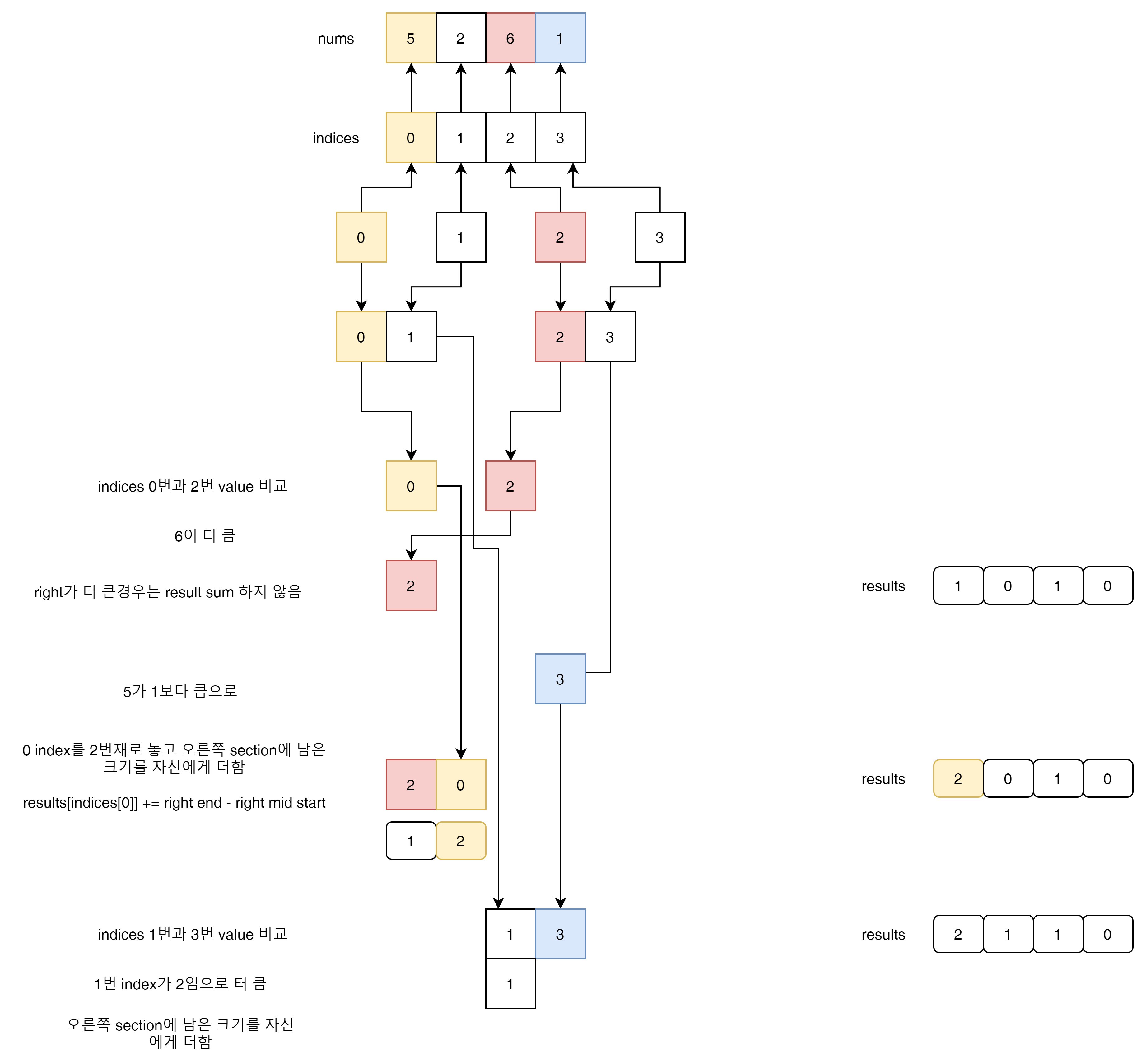
설명을 자세히 하지는 않았는데 위의 그림을 보면 indices의 nums index만 바꾸는 방식으로 nums와 results의 값 순서에 변화를 일으키지 않는 방법을 사용했다.
Time Complexity는 $$ O(N LogN) $$ 이 된다.
var countSmaller = function (nums) {
let result = new Array(nums.length).fill(0);
let indexCount = 0;
let indices = new Array(nums.length).fill(0).map(_=> indexCount++);
mergeSort(nums, result, indices, 0, nums.length);
function mergeSort(nums, result, indices, start, end) { //nums변동없음, result변동 없음, indices 변동, start point, end point exclude
if(end - start <= 1) return;
let mid = start + Math.floor((end - start) /2);
mergeSort(nums, result, indices, start, mid);
mergeSort(nums, result, indices, mid, end);
merge(nums, result, indices, start, mid, end);
}
function merge(nums, result, indices, start, mid, end){ //end exclude
let left = start;
let right = mid;
let temp = new Array();
while (left < mid && right < end) {
if(nums[indices[left]] <= nums[indices[right]]){ //큰 쪽을 우선 넣었음, 같은 값은 우측을 우선 함으로써 추가 값이 없게 처리 필요
temp.push(indices[right++]);
} else {
result[indices[left]] += end - right;
temp.push(indices[left++]);
}
}
while (left < mid) {
temp.push(indices[left++]);
}
while (right < end) {
temp.push(indices[right++]);
}
for (let i = start; i < end; i++) {
indices[i] = temp[i - start];
}
}
return result;
};'Problem Solving' 카테고리의 다른 글
| Reaching Points (0) | 2021.06.26 |
|---|---|
| Longest Increasing Path in a Matrix (0) | 2021.06.23 |
| Binary Search Lower Bound와 Upper Bound (0) | 2021.06.17 |
| Remove Invalid Parentheses (0) | 2021.06.14 |
| Regular Expression Matching (0) | 2021.06.13 |
