문제 내용
숫자로 구성된 Array가 있다. 해당 Array와 동일한 길이의 0으로 채워진 Array가 있을 때 연속된 Sub Array를 1 증가 시킬 수 있다면, 몇번의 Sub Array 증가 Operation이 필요한가?
접근 방법
[1,2,3,2,1]
이 있을 때 우리는 어떻게 계산을 해야하는가?
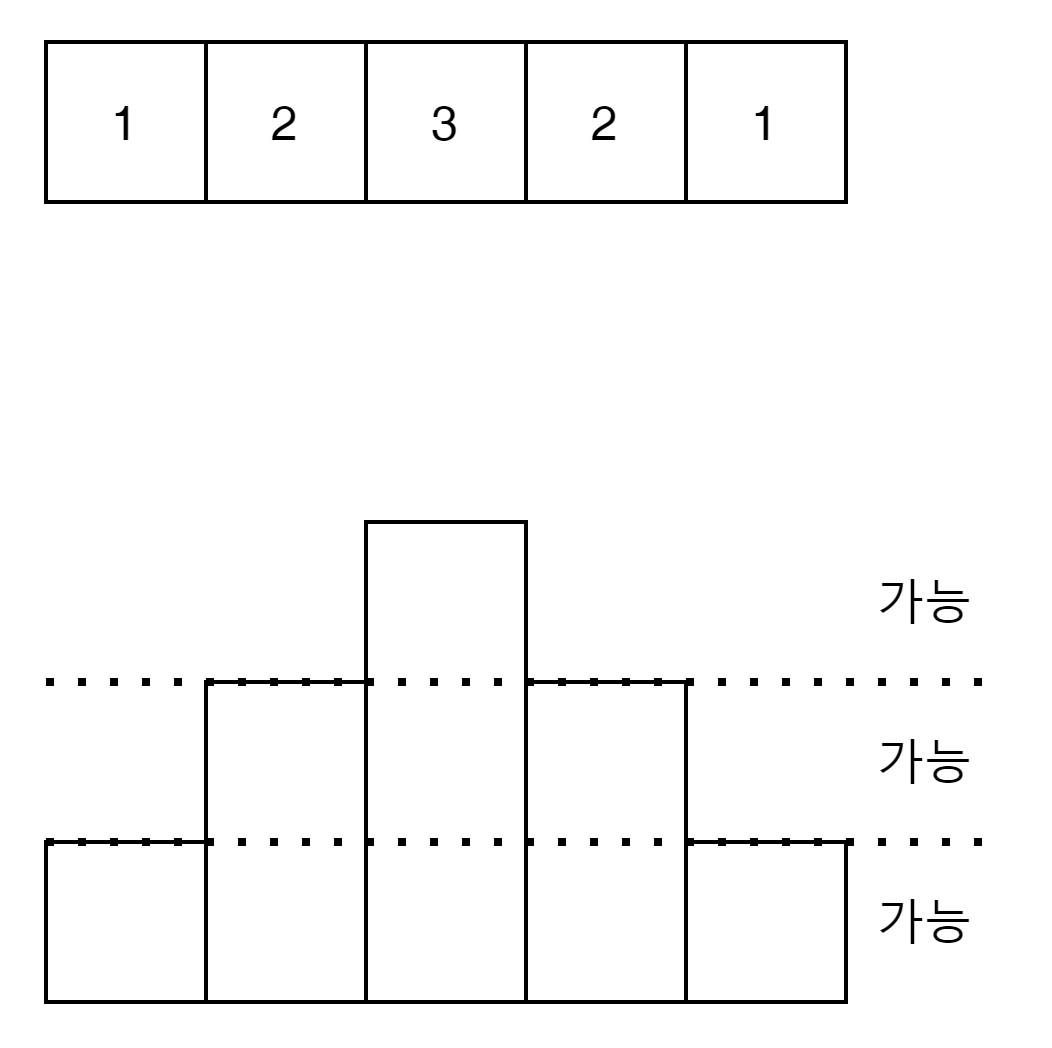
전체 Array에 1을 한번 채워서 [1,1,1,1,1]을 만들고 다시 중간에 [0,1,1,1,0]을 채우고, 마지막으로 [0,0,1,0,0]을 채우면된다.
그럼 조금더 복잡한 값을 생각해 보자.
[3,1,5,4,2]를 계산해 보자.

가장 하단에서 부터 11111을 채우고,
다시 2단에서 10111을 채워 넣어야 한다. 그런데 연속된 Sub Array를 1 증가시키는 Operation만 가능함으로
10000, 001111 이렇게 2번의 Operation이 필요하다.
다시 10110이 필요 하니까 10000, 00110 2번이 필요하고
다음으로 001100
마지막으로 00100 이렇게 총 7번의 Operation으로 관리가 가능 한것을 알 수 있다.
이것을 순선대로 프로그램 한다면,

이런 형태로 계산이 가능하다. 이것을 프로그램으로 짜게 되면 Time complexity는
$$ O(maxNum * Arr.length) $$
가 된다.
문제의 Constraints가 최대 Array 길이 $ 10^5 $ 에 Arr.lenght는 $ 10^5 $ 이기 때문에 총 $ 10^{10} $ 회의 Time complexity가 필요하다.
최적화가 필요하다.
Divide Conquer
해당 문제는 0을 기준으로해서 Array의 연속성이 깨지게 된다.
해당 부분을 Divide Conquer를 이용해서 최적화 가능하다.
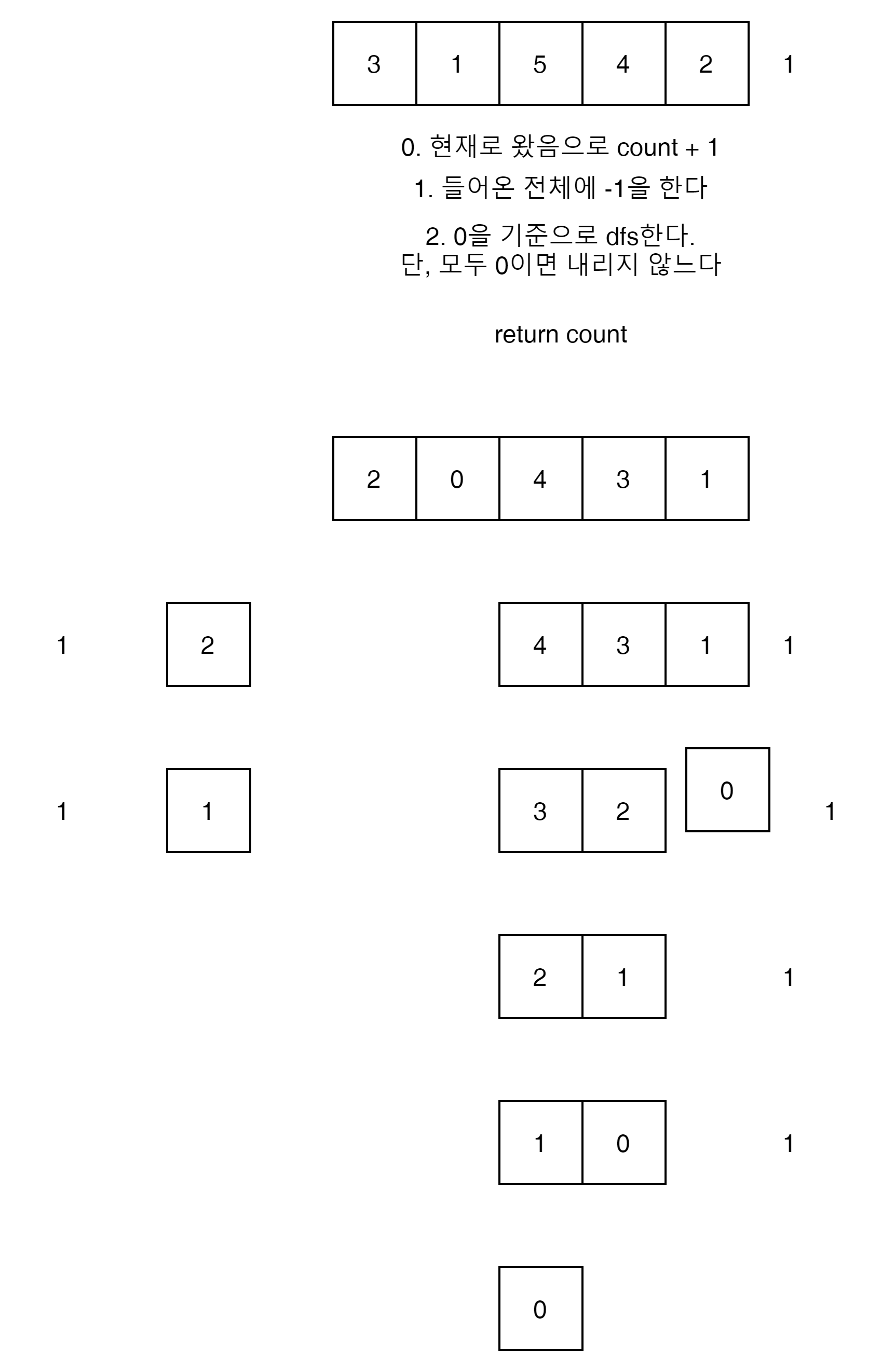
상위와 같이 0을 기준으로 Array를 Subarray로 분리하게 함으로써 Array의 모든 length를 search할 필요 없게 할 수 있다.
$$ O(maxNum * Log Arr.length) $$
가 가능하다. 그럼에도
$ 10^5 * Log 10^5 $ 는 여전히 큰 값이다.
var minNumberOperations = function(target,start = 0, end = target.length) {
let min = Number.MAX_SAFE_INTEGER;
for (let idx = start; idx < end; idx++) {
min = Math.min(min, target[idx]);
}
return helper(target, min);
function helper(target, min, start = 0, end = target.length) {
// console.log(target, min,start, end);
if(end - start === 1) return target[start];
let count = min;
let sub = -1;
let subMin = Number.MAX_SAFE_INTEGER;
for (let idx = start; idx < end; idx++) {
target[idx] -= min;
if(0 < target[idx] && sub < 0) {
sub = idx;
} else if(0 <= sub && target[idx] === 0){
count += helper(target,subMin,sub,idx);
sub = -1;
subMin = Number.MAX_SAFE_INTEGER;
}
if(0 <= sub){
subMin = Math.min(subMin, target[idx]);
}
}
if (0 <= sub) {
count += helper(target,subMin,sub,end);
}
return count;
}
};One Pass - Stack
문제를 조금 다른 시선으로 볼필요가 있다.
아래 내용을 보자.

이 문제의 답은 3이다. 가장 높은 값을 갖는 Max value와 동일하다.
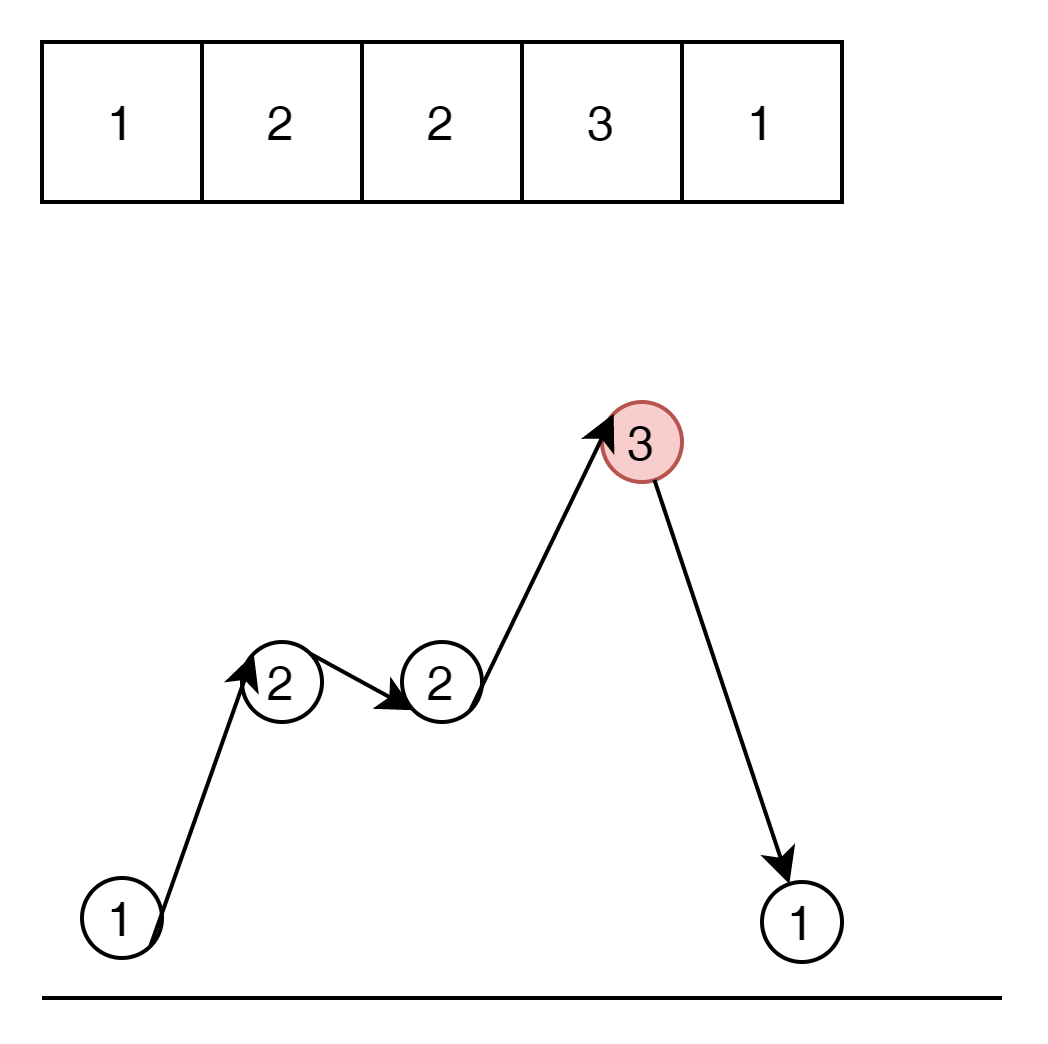
이 경우도 마찬가지로 3이 답이된다.
즉, 연속된 숫자의 그룹에서는 Max의 값이 정답이 된다.
그럼 이것을 2개 붙여 보자.

답은 6이 된다. 양쪽이 0으로 분단 되었기 때문이다.
만약에 이 0이 1이었다면 어떨까?

답은 5가 된다. 왜냐하면 최초에 11개의 Array를 1로 한번 채울 수 있기 때문이다. 그렇기 때문에 두번째 Array에서는 2번의 Operation만 필요하다.
여기서 우리는 2가지를 알 수 있다.
- 연속된 Subarray의 최대 Count 횟수는 Max 값이 답이 된다.
- 앞서 min 값이 이미 채워진적이 있다면 max - min이 답이된다.
이것을 바탕으로 아래의 문제를 다시 확인해 보자.

상위와 같이 숫자의 변화를 보면, 답을 만드는데 중요한 값은 3과 5 두개라는 사실을 알 수 있다.

그리고 이 3과 5는 3 + 5 - 1이 답이 된다.
여기서 이 1이 min이 되기 때문이다.

이것을 다른 문제로 바꾸어 본다면 stock 문제와 동일하게 된다.
한번 주식을 사고 한번 주식을 팔수있다. 가장 높은 이익은 얼마인가?
https://leetcode.com/problems/best-time-to-buy-and-sell-stock-with-transaction-fee/
Stack을 사용해서 가장 낮은 값에서 가장 높은 값을 빼면 되는 문제이다.
위의 문제를 Stack으로 생각해 보면 아래와 같다.

0은 3보다 작은가? 그렇다.
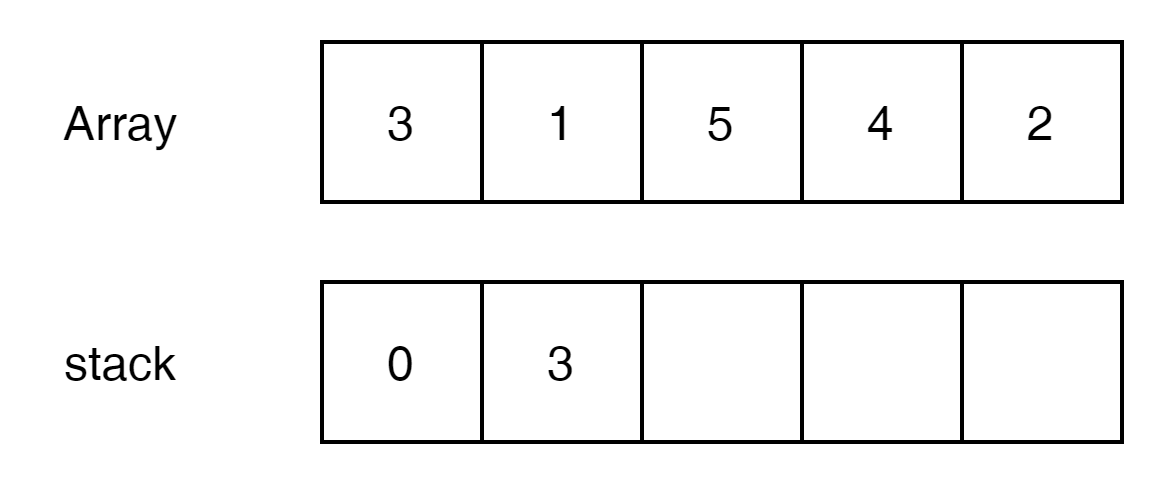
3은 1보다 작은가? 아니다. 연속된 Array의 Max값은 3이된다.
즉,
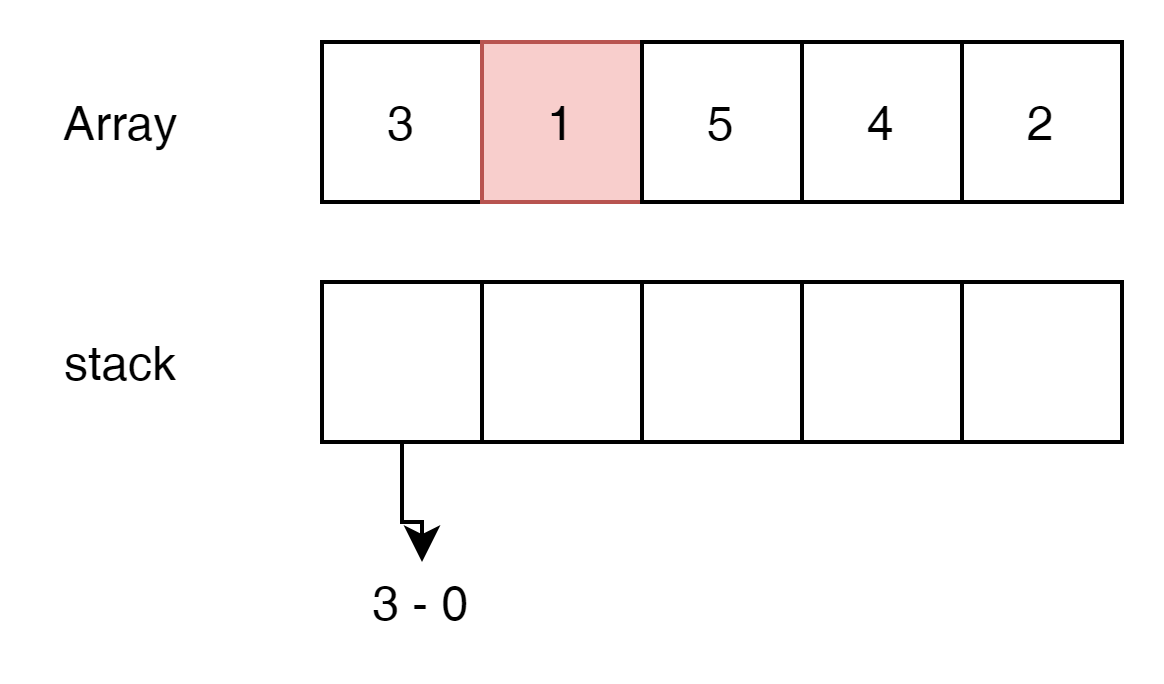
stack이 clear되고 가장 높은 stack의 peek와 0 값을 빼주면 된다. result = 3
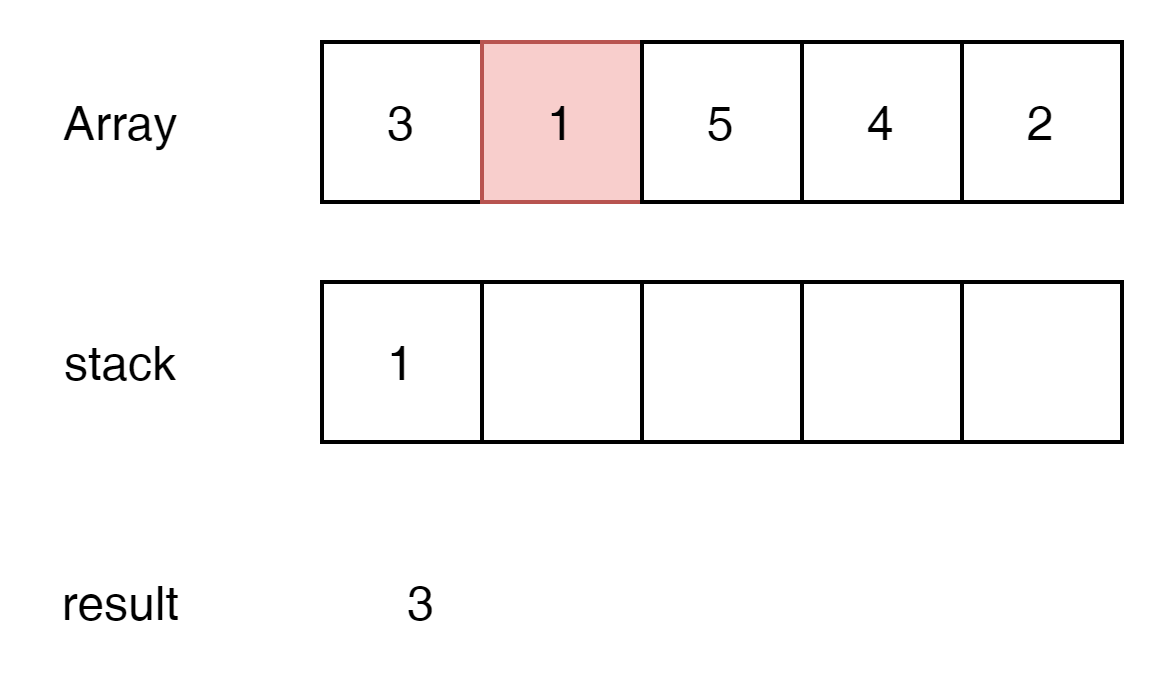
1을 stack에 넣고 다시 max를 찾아 보자
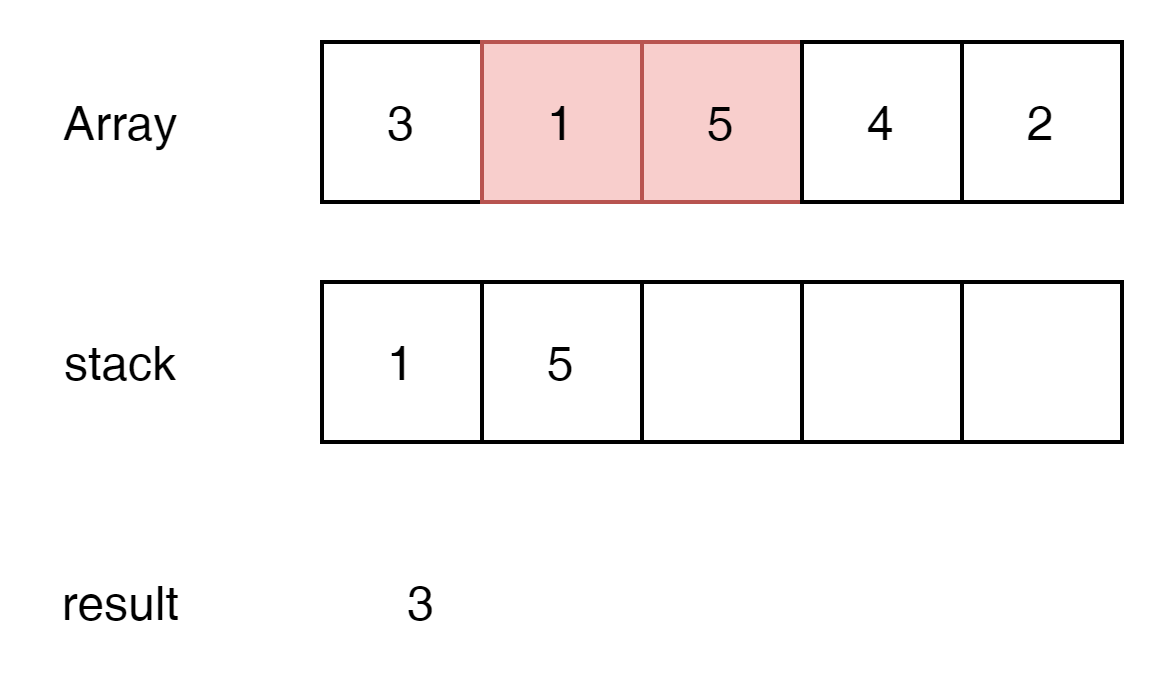

4는 5보다 작다. Max를 찾았다. 5-1을 result에 넣어 주자.

이제 stack에 4를 넣어주자.
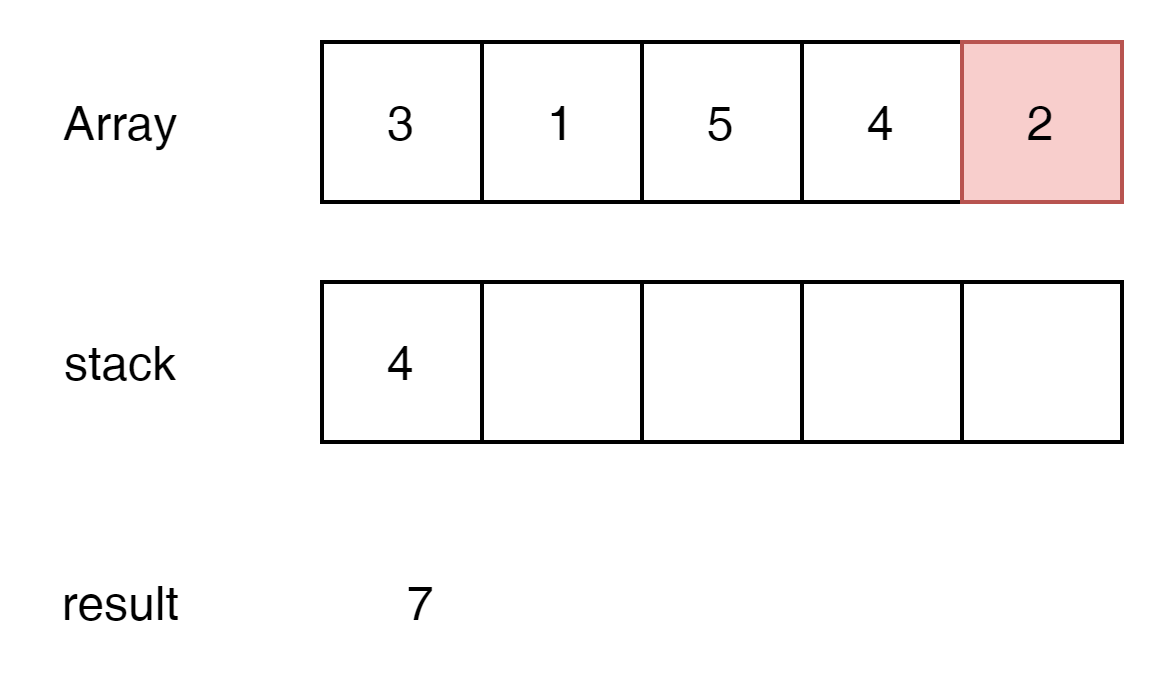
4는 2보다 작지 않다 stack을 clear 시켜준다. peek와 0 값이 같음으로 result는 7 유지
같은 방법으로 2역시

peek와 result가 같음으로 0이 된다.
최종적으로 답은 7이다.
var minNumberOperations = function(target) {
let stack = new Array();
let result = 0;
stack.push(0);
for (let i = 0; i < target.length; i++) {
if (stack[stack.length - 1] > target[i]) {
result += stack[stack.length-1] - stack[0];
stack.length = 0;
}
stack.push(target[i]);
}
if (0 < stack.length) {
result += stack[stack.length-1] - stack[0];
}
return result;
};Time Complexity는 $ O(array length) $ 가 된다.
대신에 stack을 사용했음으로 Space Complexity는 $ O(array length) $ 가 된다.
One Pass
위에서 Stack처리를 보면 아래와 같이 계산이 단순화 될 수 있음을 알 수 있다.


즉 앞선 값이 현재의 값보다 작다면 그 차의 누적이 답이 된다.
target[current Index] - target[pre Index] > 0
두개의 값의 차가 0보다 크다면 result sum 그외는 모두 0으로 처리 하면 된다.
var minNumberOperations = function(target) {
let result = target[0];
for (let i = 1; i < target.length; i++) {
result += Math.max(target[i] - target[i-1], 0);
}
return result;
}Time Complexity는 $ O(array length) $ 이고,
Space Complexity는 $ O(1) $ 가 된다.
'Problem Solving' 카테고리의 다른 글
| Valid Perfect Square (Newton's Method) (0) | 2021.07.27 |
|---|---|
| 132 Pattern (0) | 2021.07.25 |
| 990. Satisfiability of Equality Equations (0) | 2021.07.22 |
| Average Selling Price (0) | 2021.07.20 |
| Find Center of Star Graph (0) | 2021.07.14 |
