문제 내용
좌측, 우측, 가운데 순으로 숫자의 크기가 결정되는 값이 있는가를 확인 하는 문제이다.
예를 들자면
[3,1,4,2]의 경우 좌측 값 1 우측 값 2일 경우 가운데 4의 값이 가장 큼으로 132패턴을 만족한다.
접근 방법
모든 수를 순회하는 방법이 가장 쉽다.
예를 들자면 왼쪽을 left 오른쪽을 right라고 했을 때,
left와 right를 고정하고 가운데를 순회 시키면 된다.
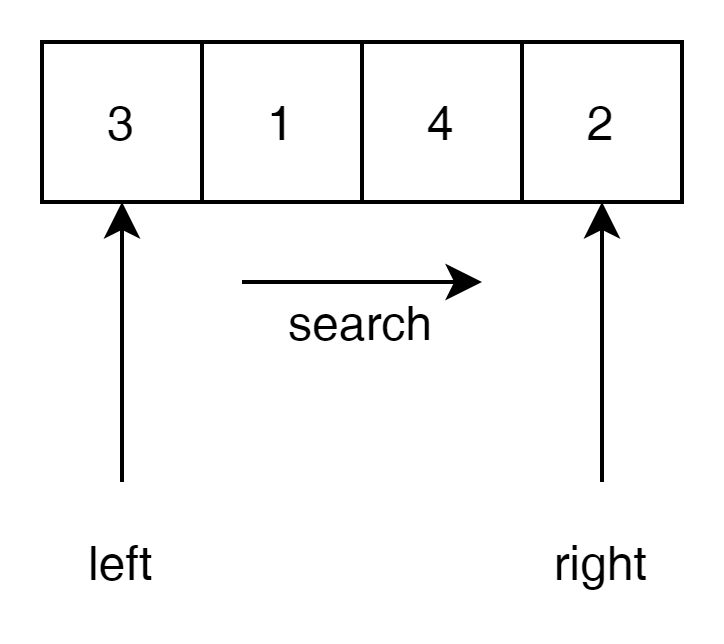
이렇게 되면 left, right full search로 n^2 그리고 가운데 search 횟수 포함해서 $ O(n^3) $ 이 되게 된다.
이것을 최적화 하기위해서 min 값을 관리할 수 있다.

예를 들자면 index 2 값 4일때 min은 1이라는 것을 알 수 있다.
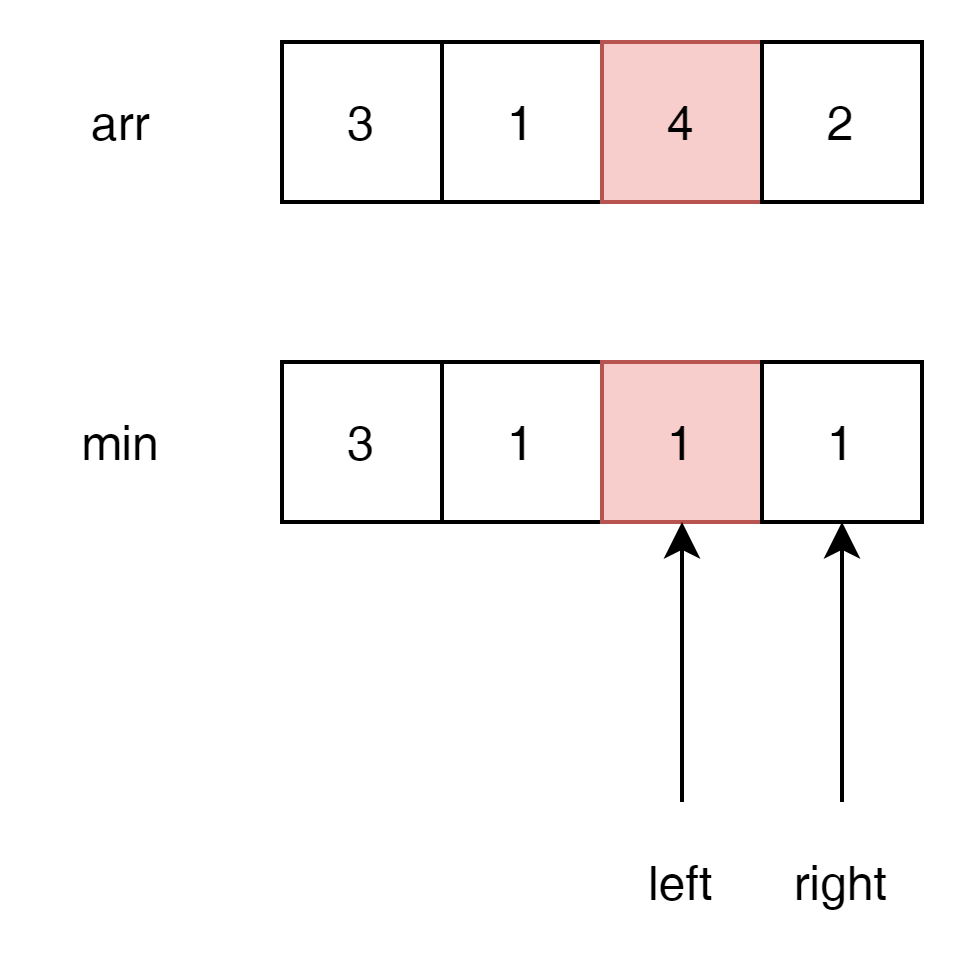
left와 right를 순회하면서 arr[right] < arr[left] 이고 min < arr[right] 이면 답이 된다. left와 right를 full search함으로
$ O(n^2) $ 가 된다.
위의 특성을 이용해서 stack을 사용할 수 있다.
Stack
우선 min에 대한 특징을 알아 보자.
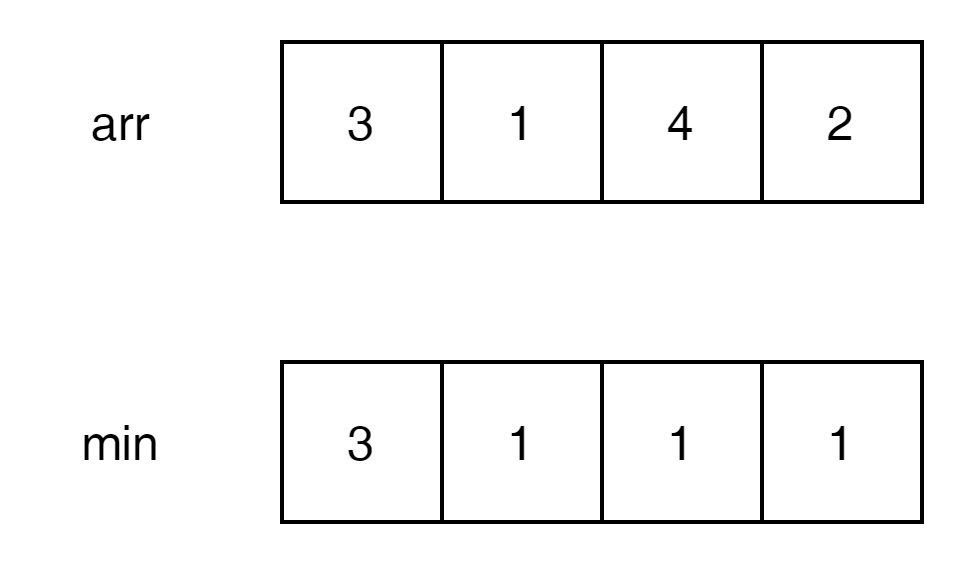
min의 array는 오른쪽으로 갈 수로 낮은 값으로만 이루어진다.
그래프로 보자면

이런 형태이다.
특정 index에서의 min값은 현재 위치 좌측은 같거나 더 큰값으로만 이루어 질 수 있다.
그렇기 때문에 본 문제의 특성이 좌측값 즉 min값이 가장 작은 값이어야 함으로 right의 값이 min과 같거나 작은 값은 의미가 없다고 볼 수 있다.
이 특성을 이용해서 Stack을 사용해 보자.
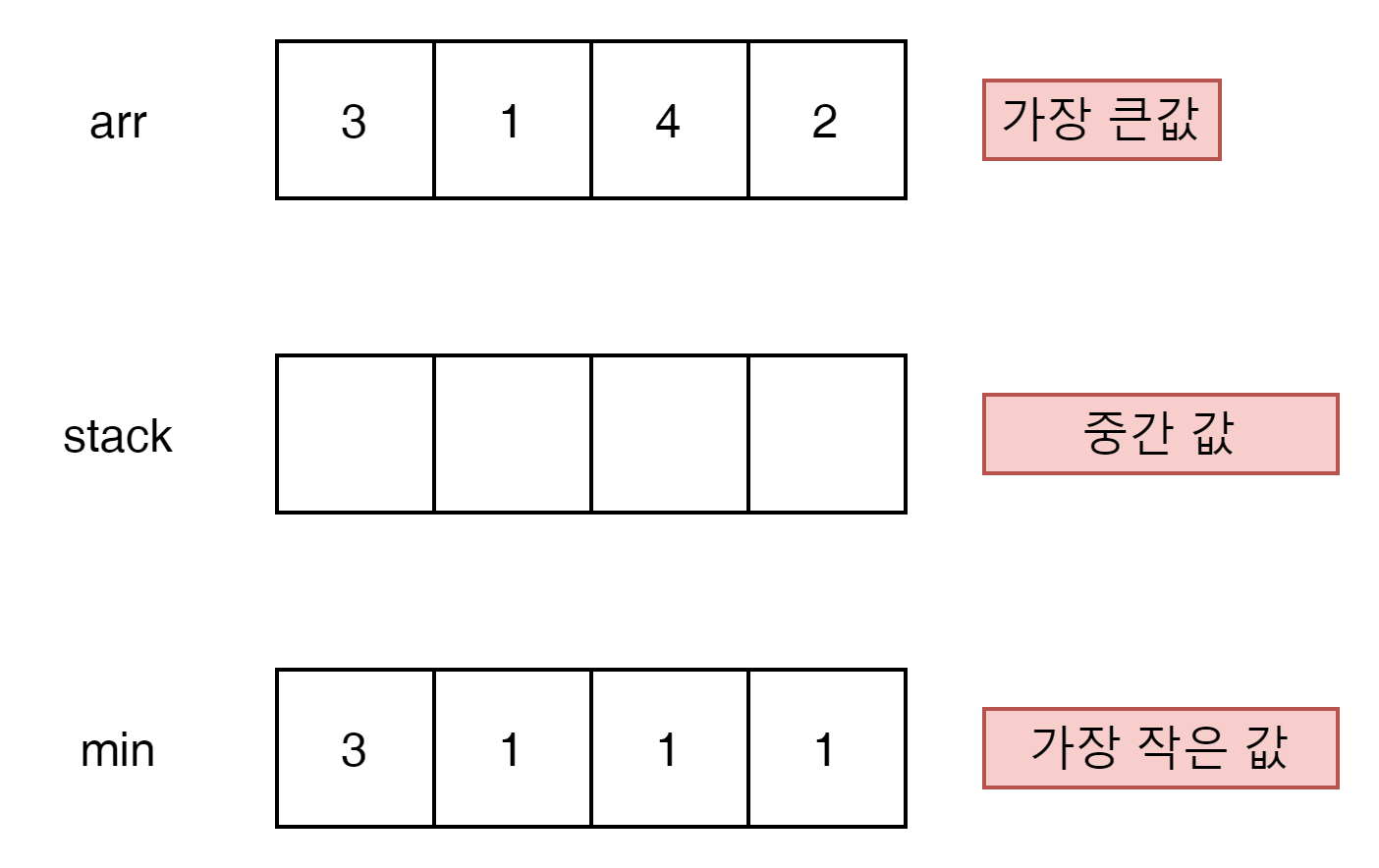
이렇게 3개의 array가 있다.
가장 우측인 2부터 시작하자.
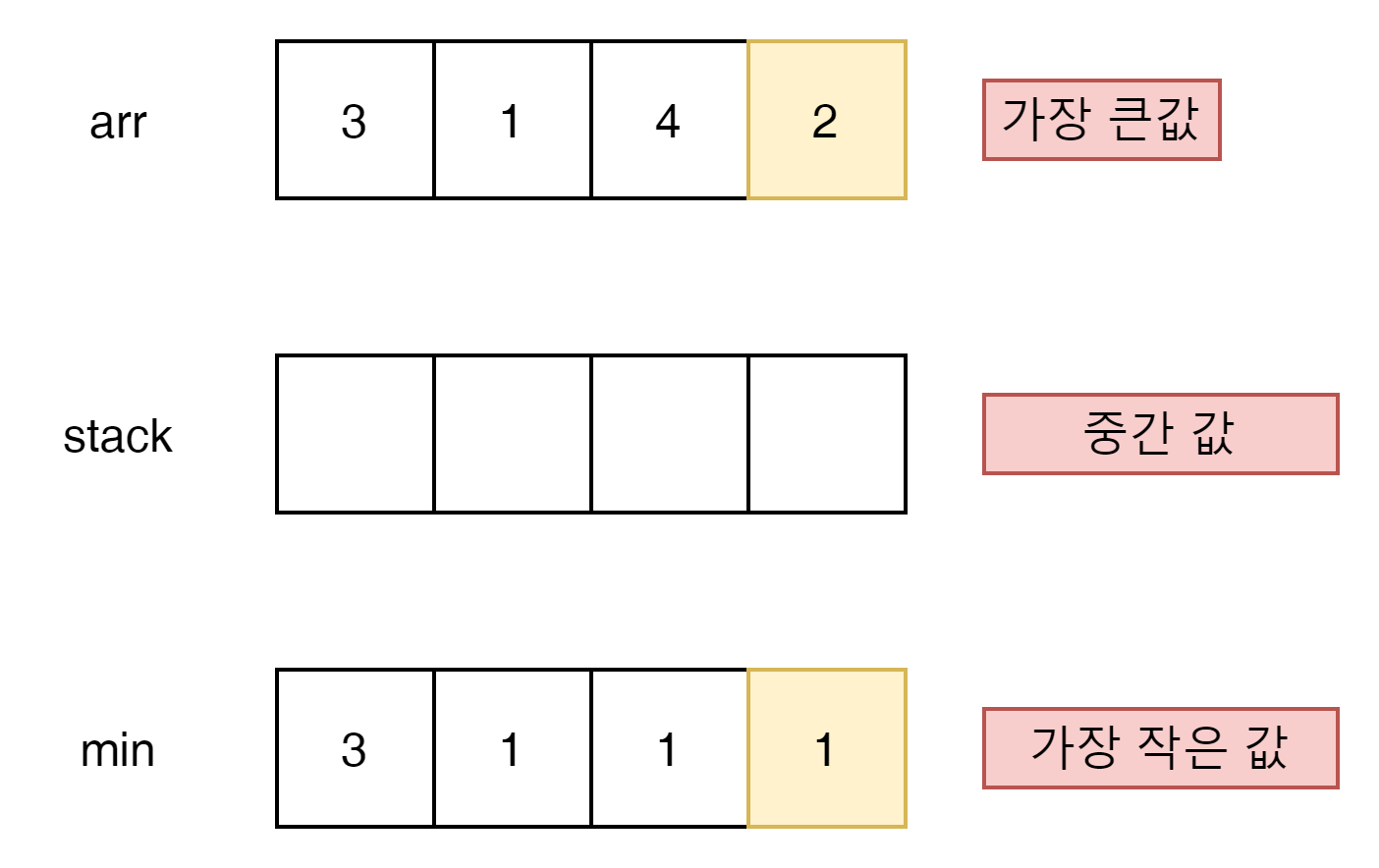
min 값 1보다 arr 값 2가 더 크다. 그러나 중간 값이 없음으로 index 3번은 답이 될 수 없다.
일단 2가 min 값보다 큼으로 stack에 2를 넣는다.

가장 큰값은 4이고 min은 1이고 중간의 값 2가 존재 함으로
- min < stack top < arr[currnet]
가 성립함으로 답은 true가 된다.
그럼 한 문제를 더 확인해 보자.
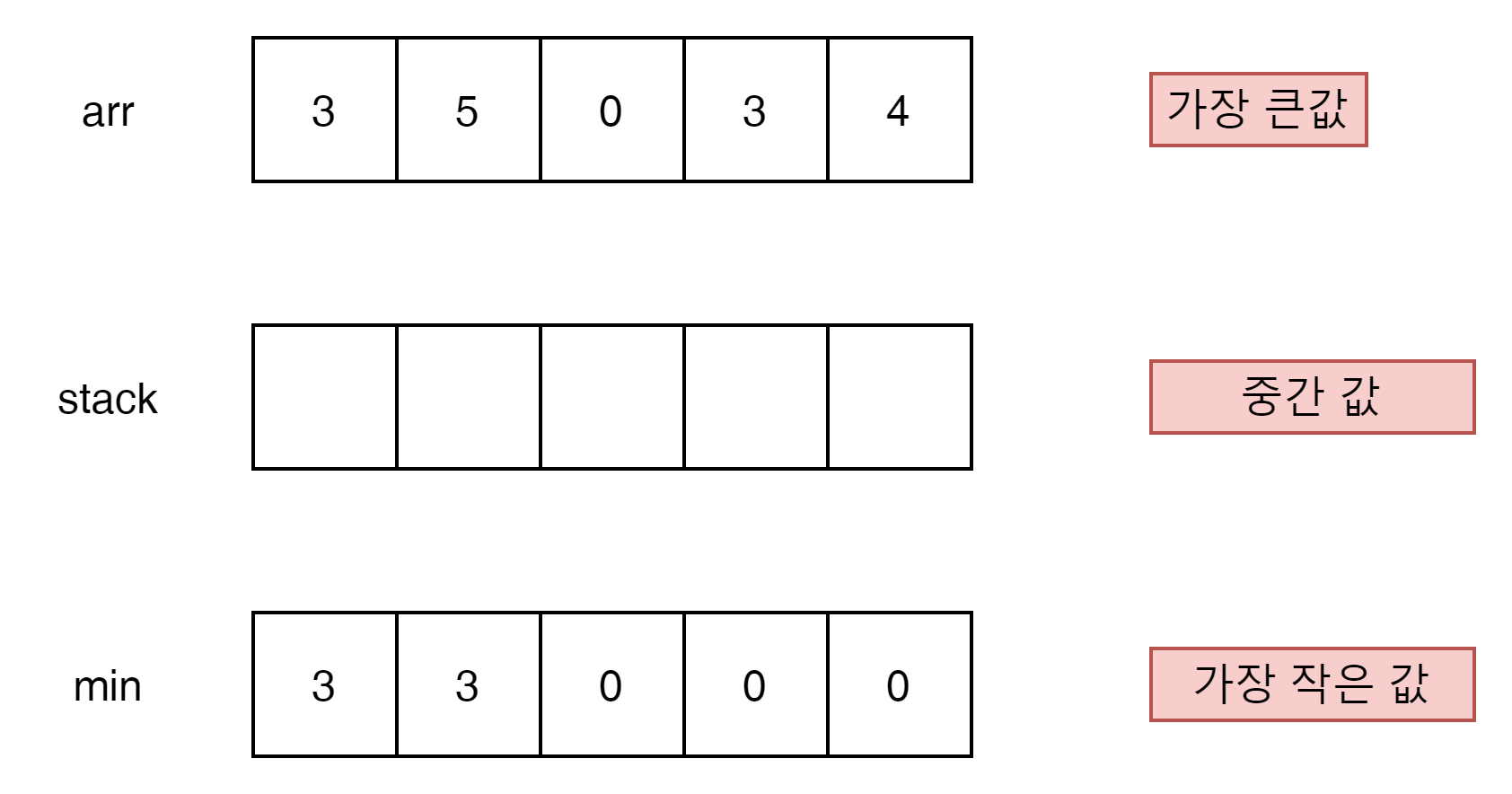
우측 부터 차례대로 가보자.

0 < 4 를 만족하지만 stack에 아무것도 없음으로, stack에 값을 넣고 왼쪽으로 이동하자.

0 <3을 만족하지만 4< 3을 만족 하지 못한다. 3이 아직 min보다 큼으로 답의 가능성이 있다. stack에 넣는다.

0 < 0을 만족하지 않음으로 답의 가능성이 없다. stack에 넣지 않고 좌측으로 옮긴다.

3 < 5가 성립한다. 그러나 top인 3이 min과 같음으로 3은 답의 가능성이 없다. 좌측은 무조건 3과 같거나 더 큰 값이 min이 될 것이다.
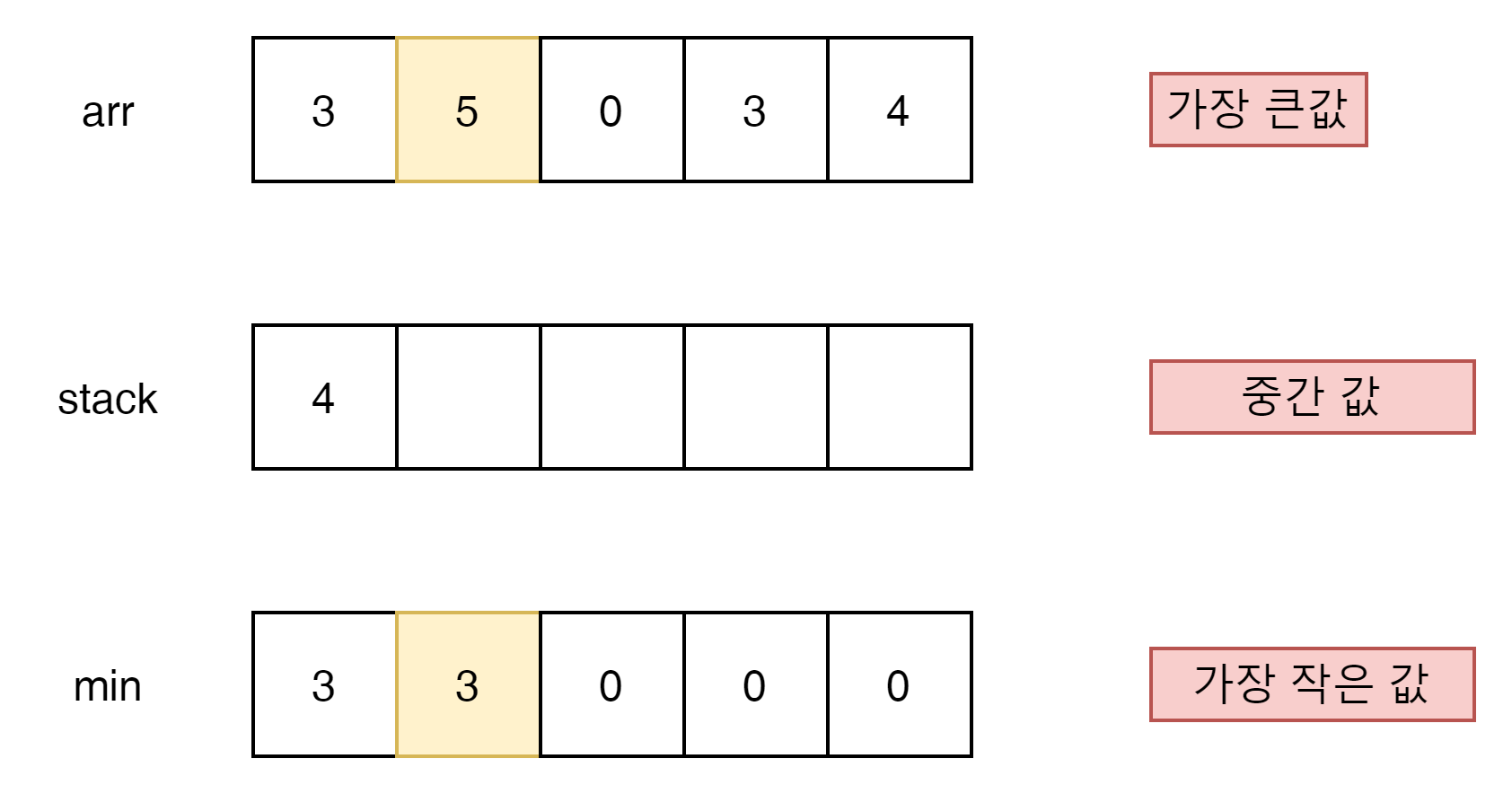
3 < 5를 만족하고, 3 < 4 < 5가 만족함으로 답이 된다.
stack을 이용해서 한번만 우측에서 좌측으로 이동함으로 $$ O(N) $$ 이다.
var find132pattern = function(nums) {
let mins = new Array(nums.length);
let stack = new Array();
mins[0] = nums[0];
for (let i = 1; i < nums.length; i++) {
mins[i] = Math.min(nums[i], mins[i - 1]);
}
for (let j = nums.length - 1; 0 < j; j--) {
if (nums[j] > mins[j]) {
console.log(j, stack, nums[j], mins[j]);
while (0 < stack.length && stack[stack.length - 1] <= mins[j]) {
stack.pop();
}
if (0 < stack.length && stack[stack.length - 1] < nums[j]) {
return true;
}
stack.push(nums[j]);
}
}
return false;
};
'Problem Solving' 카테고리의 다른 글
| Super Egg Drop (0) | 2021.07.30 |
|---|---|
| Valid Perfect Square (Newton's Method) (0) | 2021.07.27 |
| Minimum Number of Increments on Subarrays to Form a Target Array (0) | 2021.07.24 |
| 990. Satisfiability of Equality Equations (0) | 2021.07.22 |
| Average Selling Price (0) | 2021.07.20 |
