문제 내용
주어진 number의 값이 $ x^2 $ 형태로 표현될 수 있는 수 인지 확인하시오.
단, sqrt method는 사용하면 안됨
접근 방법
가장 쉬운 방법은
1에서부터 number까지 자기자신을 곱해서 원하는 값이 되는지 확인하면 된다.
var isPerfectSquare = function(num) {
if(num===1) return true;
for(let i = 1; i*i <= num; i++) {
if(i*i === num) return true;
}
return false;
};Time Complexity 상으로는 $ O(N) $ 이 된다.
그럼 조금더 빠른 방법을 고민해 보자.
위의 프로그램에서 우리가 알 수 있는 것은
- num/2 보다 큰 값이 x가 될 수는 없다.
즉, number가 4일 경우 3이 답이 될 수는 없는것이다. 9일 경우는 4가 답이 될 수 없다.
이것을 이용해서 number가 16일 경우 답을 찾아보자.
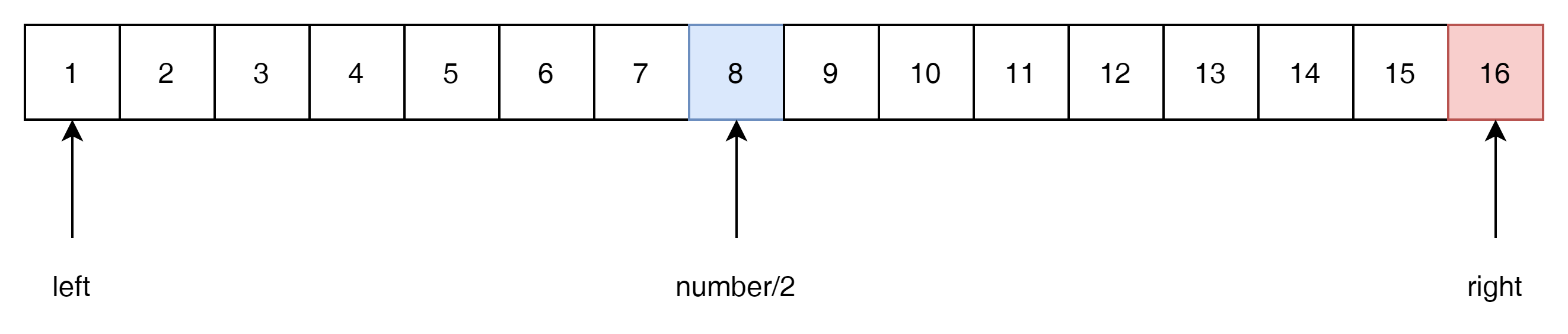
left는 1이고 right는 16이다. num/2는 답이 될 수도 있고 안될 수도 있다.
여기서 8 * 8이 number보다 더 큰 값이 된다.
$$ 8^2 > 16 $$
8의 우측은 답의 대상이 될 수 없다.

right의 위치를 8로 옮겨준다.
다시 한번 더 num/2를 진행해 보자. 단, 8역시 답의 대상이 되지 못하다는 것을 알았음으로 right의 위치를 한칸 밑으로 옮겨 준다.

center는 number/2이고 이 값은 4 즉 답이 된다.
9도 마찬가지다.

number가 10이면 어떨까?

$ 4^2 > 10 $ 이 됨으로 결국 답을 찾지 못하게 된다.
var isPerfectSquare = function(num) {
if(num < 2) return true;
let left = 2;
let right = num;
while(left <= right){
let center = left + Math.floor((right - left)/2);
if(center * center === num) return true;
if(num < center * center) right = center - 1;
if(center * center < num) left = center + 1;
}
return false;
};실 속도는 처음 것과 크게나지는 않지만 시간 복잡도는
$$ O(LogN) $$
이 된다.
이런 점진적 답을 찾는 방법을 "뉴튼의 방법"이라고 한다.
뉴튼의 방법
매번 그렇지만 수학을 잘 못해서 그런가 이런 수학적 접근 방법은 쉽지않다.
최대한 이해한 만큼 이곳에다가 글을 남겨 보고자 한다.
x의 차수가 2이상인 곡선의 방정식은 아래와 같은 형태를 갖는다.

만약에 x의 위치를 구하기 어렵다면 어떻게 해야할까?

이 점근적 근의 근삿값을 구하는 방법을 뉴튼의 방법 또는 Newton's Method라고 부른다.
우선 우리의 문제를 define해보자.
우리가 알고자 하는 $ number = x^2 $ 으로 나타낼 수 있다.
이것을 f(x) 형태로 변경하면 $ f(x) = x^2 - number $ 이라고 표현이 가능하다.
이것은 y의 값이 0일때 x의 값을 찾는 그래프로 표현 가능하다.

여기에서 x의 값은 무었일까? 이 근삿값을 구하면 되는데
이 근삿값을 구하는 아이디어는 아래와 같다.
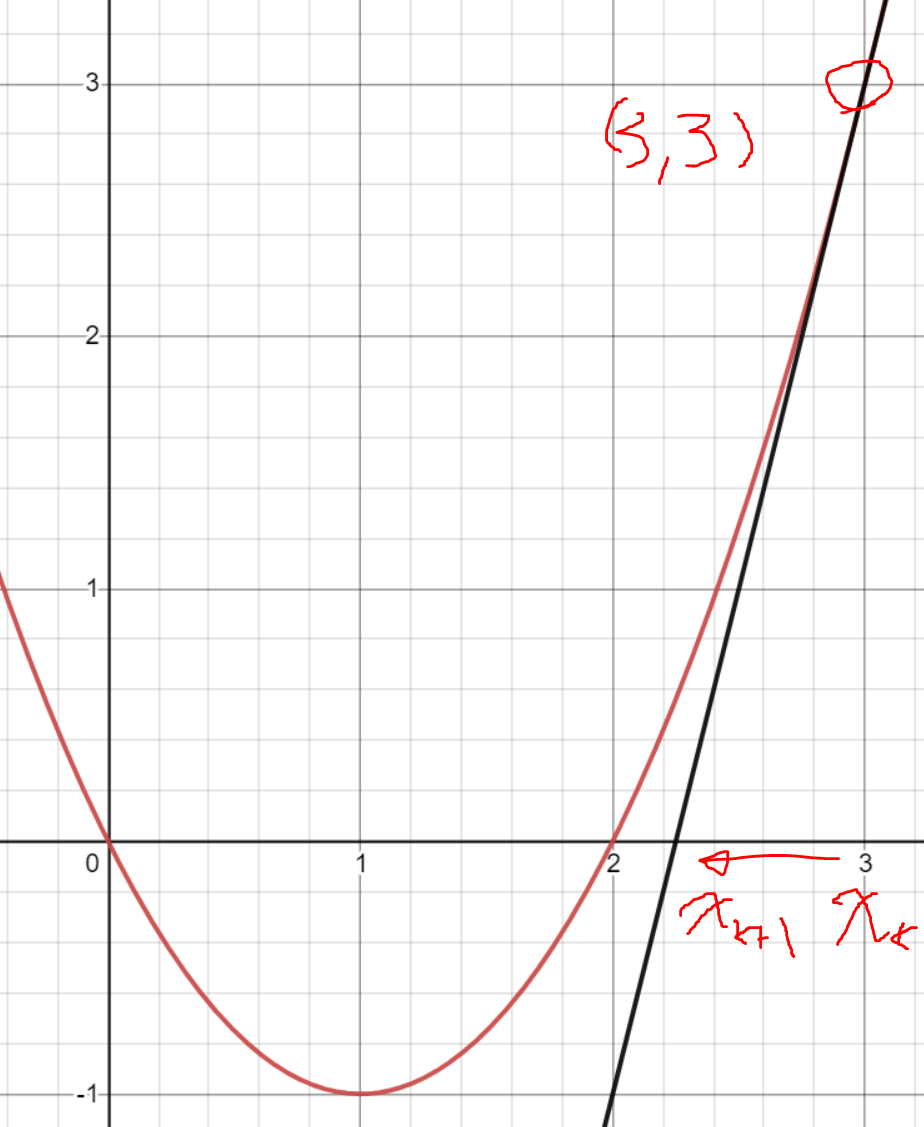
$ y = x^2 - 2x $ 라는 2차수 공식이 있을 때 (3,3)을 접점으로 하는 접선 $ y = 4x-9 $이고 이 공식을 이용해서 $ x_{k+1} $을 구한다.
그리고 다시 $ x_{k+1 +1} $을 구해서 해당 값이 목표하고자 하는 값에 가까워 졌는지를 확인하는 방식이다.
그럼 접선은 어떻게 구하면 될까?
우선 직선의 방정식을 알아보자.
- 기울기와 한점을 알 경우 직선의 방정식 : $ y - y_1 = m(x - x_1) $
이 공식을 이용해서 우리가 알고 싶은 $ x $ 만 뽑아내 보자.
우리가 알고 싶은것은 접선이 생기는 점의 좌표 (x_1, y_1)이 목표가 아니기 때문이다.
우리가 알고 싶은것은 (x, 0) 이다.
$$ \frac{y - y_1}{m} = x - x_1 $$
$$ \frac{y - y_1}{m} + x_1 = x $$
$$ \frac{y - y_1}{m} + x_1 = x $$
이 된다. 앞서 우리가 알고 싶은 y는 0이라고 했음으로,
$$ \frac{- y_1}{m} + x_1 = x $$
이 된다.
이제 기울기 m은 어떻게 구할 수 있을까? 그것은 $ f(x)' $ 로 나타낼 수 있다. 미분은 $ \delta{y} / \delta{x} $ 이기 때문이다.
$$ x = x_1 - \frac{y_1}{m} $$
$$ x = x_1 - \frac{f(x)}{f(x)'} $$
로 표현 가능하게 된다.
이제 다시 본론으로 돌아가서 우리가 찾고자 하는 공식은
$$ f(x) = x^2 - number $$
였다.
이 공식을 통해서 기울기 m을 알 수 있도록 미분을 진행해 보자.
$$ f(x)' = 2x $$
가 된다.위의 공식에 추가적으로 대입해 보자.
$$ x = x_1 - ( \frac{x^2 - number}{2x} ) $$
$$ x = x_1 - \frac{x^2}{2x} + \frac{number}{2x} $$
$$ x = x_1 - \frac{x}{2} + \frac{number}{2x} $$
$$ x = \frac{x_1}{2} + \frac{number}{2x_1} $$
$$ x = \frac{1}{2} * ( x_1 + \frac{number}{x_1}) $$
이 된다.
여기서 중요한 것은 x의 시작값을 어디로 줄것이냐? 이다.
어디서 부터 시작해도 문제는 없지만 가장 간단한 방법은 number/2로 시작하는 것이다.
이것을 코드로 옮기면 아래와 같다.
var isPerfectSquare = function(num) {
if(num < 2) return true;
let x = num/2;
while(x * x > num){
x = (x + num/x) / 2 | 0;
}
return (x * x === num);
};여기서 '| 0' Bitwise Operator를 사용하는 이유는 floating 연산처리를 하지 않기 위해서 이다.
Math.floor 또는 Math.trunc와 동일한 결과를 낸다.
https://stackoverflow.com/questions/7487977/using-bitwise-or-0-to-floor-a-number
'Problem Solving' 카테고리의 다른 글
| 2진수 최 좌측 1자리 찾기 (0) | 2021.08.02 |
|---|---|
| Super Egg Drop (0) | 2021.07.30 |
| 132 Pattern (0) | 2021.07.25 |
| Minimum Number of Increments on Subarrays to Form a Target Array (0) | 2021.07.24 |
| 990. Satisfiability of Equality Equations (0) | 2021.07.22 |
