문제 내용
N개의 달걀이 있다.
K 층으로 이루어진 빌딩이 있다.
달걀은 해당 빌딩의 특정 층 F에서 깨지기 시작한다.
N개의 달걀을 이용해서 F 층을 찾을 수 있는 가장 적은 시도 횟수를 갖는 방법 횟수를 찾아라
접근 방법
문제 자체를 이해하는데 굉장히 난해했다.
이 문제는 굉장히 오래된 문제인데, 아직도 Youtube나 Article을 보면 적당히 설명이 된 글이 많지 않았다.
어떤 글은 너무 쉬운 부분만 설명하거나, 또 어떤 글은 굉장히 어려운 말로 설명되어있었다.
우선 문제를 이해하자.
5층으로 이루어진 빌딩이 있고 달걀 1개가 주어졌다면 몇번 욺직여야 f를 찾을 수 있을까?

한개의 달걀로 f를 무조건 찾을 수 있는 방법은 5층에서 부터 2층사이에 달걀을 던지면 안된다는 것이다. 어디서 깨지더라도 답을 찾을 수 없기 때문이다.
- 이 문제의 key는 어떠한 경우에도 주어진 달걀로 f를 찾을 수 있어야 한다는 것이다.
달걀하나로 찾을 수 있는 방법은 1층에서 부터 달걀을 떨어 뜨려 보는 것이다.

만약 5층에서 달걀이 깨진다고 하면 5층이 f가 된다.
이것으로 알 수있는 기본 Condition은 다음과 같다.
- 달걀이 하나일때 욺직이는 Move 수는 층수와 동일하다
만약에 층이 1나일때는 어떨까?

달걀이 아무리 많아도 1층 즉 한번의 Move로 모든 점검은 끝이 난다.
- 1층은 달걀의 수와 상관없이 Move수는 1이다.
그럼 0층이면?
- 0층은 달걀의 수와 상관없이 Move수는 0이다.
그럼 이제 어떠한 경우라도 가장 적은 달걀을 희생시키면서 찾을 수 있는 Move수를 생각해 보자.
나는 이 부분을 이해하는데 굉장히 많은 시간을 투자했다.
어떤 수를 찾기위해 Move하는 최소의 수를 나는 Binary Search라고 생각했다.
예를 들어서 5층에서 4라는 f를 찾기 위해 사용되는 최소 Move수는?

3층을 한번 확인하고 만약에 깨지면 아래로 안깨지면 위로 한번 더 move하면 된다.
f가 4라고 생각하면 2번의 move로 4를 찾을 수 있다.
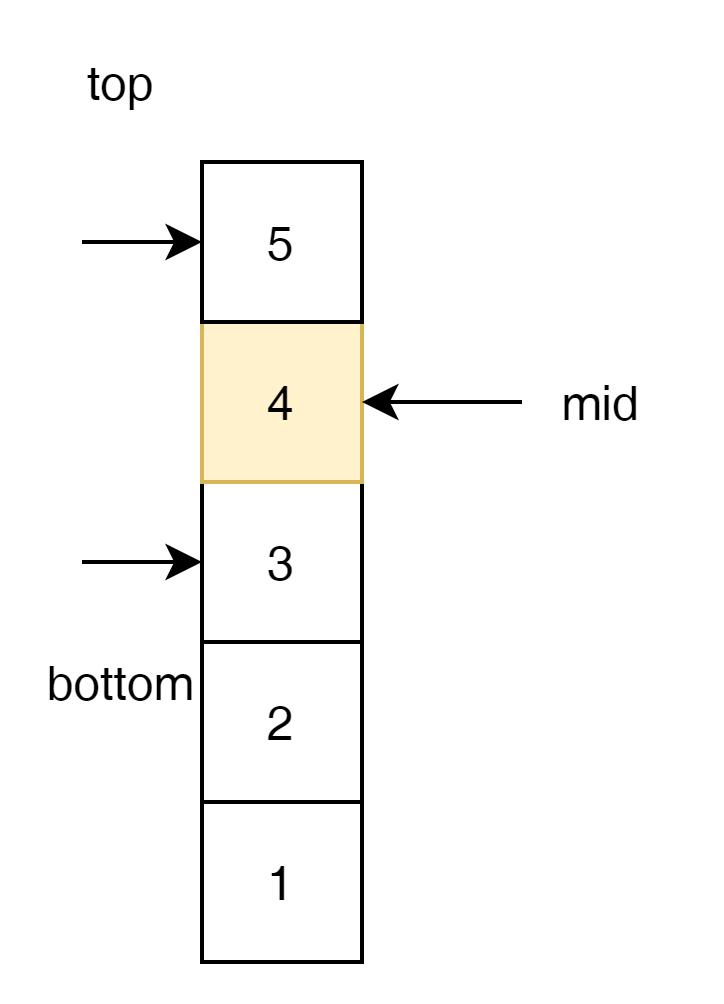
만약에 5가 답이라고 해도 3번의 move로 답을 찾을 수 있게 된다.
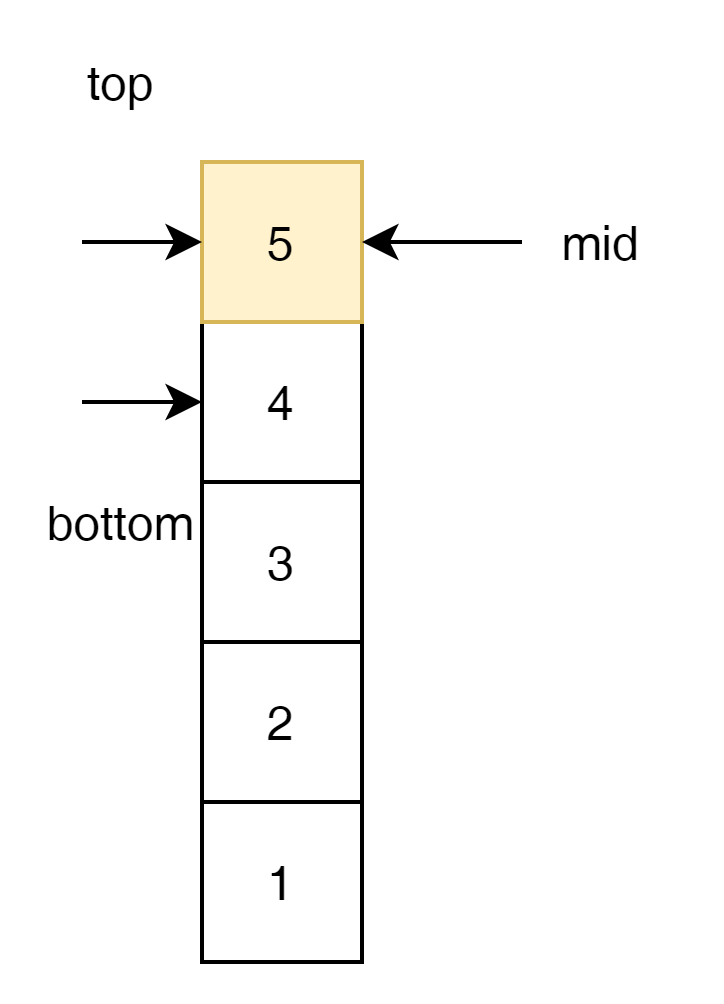
즉 달걀이 3개 주어진다면 3번의 move로 답을 찾을 수 있는 것이다.
물론 2개만 주어진다고 해도 move 수는 동일하다. 3번을 찾고 깨진다면 1,2 해서 3번 욺직이면 된다.
안깨진다고 해도 4,5 2번 더해서 3번 욺직이면 된다.
그런데 이 방법이 안된다는 걸 다음 Case에서 깨달았다.

2개의 달걀로 최대 몇번을 욺직이면 되겠는가?
Binary 방식이라고 한다면 6을 선택하고 깨지면 1에서 5를 안깨지면 7에서 10을 Search하면 된다.

반듯이 무조건 f를 찾을 수 있는 worst case를 찾아야 하니까, 6에서 달걀이 깨지고 1에서 5까지 5번을 move해서 2개의 달걀로는 6번의 move가 끝이라고 생각했다.
하지만 worst case는 4였다.
그것은 바로 아래와 같은 방법이 가능 했기 때문이다.

4에서 안깨지면 7을 7에서 안깨지면 9를 9에서 안깨지면 10을 이렇게 4번의 move이면 10개 층을 모두 search할 수 있다. 그럼 eggs가 더 늘어나면? eggs의 갯수가 늘어나면서 사람의 머리로 최적의 위치를 잡아서 경우의 수를 구한 다는 것은 어렵다. 이 부분을 해결하기 위해서 아래와 같이 모든 경우의 수를 확인 하는 방법으로 Moves를 확인 할 수 있다.

즉 첫번째 move를 어디서 부터 시작할 것인가? 이다. 위는 한눈에 봐도 3 층에서 부터 시작하면 될것 처럼 보이긴 하지만, 높은 층으로 가면 누가 알겠는가?
그래서 모든 층을 대상으로 첫 move를 선택하는 것이다.
이제 2번재 move를 선택해 보자.
2번째 move는 깨진 달걀을 생각해 볼 수 있다.

5층에서 던졌는데 달걀이 깨졌다면, 1~4 사이에 f가 있을 수도있다.
4층에서 던졌는데 달걀이 깨졌다면, 1~3 사이에 f가 있을 수도있다.
3층에서 던졌는데 달걀이 깨졌다면, 1~2 사이에 f가 있을 수도있다.
2층에서 던졌는데 달걀이 깨졌다면, 1층에 f가 있을 수도있다.
1층에서 던졌는데 달걀이 깨졌다면, 1이 f이고 move는 1이다.
0층에서 달걀은 깨질 수 없다.
이것을 수식으로 나타내면 아래와 같다.
- drop(eggs - 1, floors - 1) : 달걀이 하나깨졌고 현지 층수 이하로 확인 필요
만약에 안깨졌다면 어떨까?

5층에서 던졌는데 달걀이 안 깨졌다면, f가 있을 수 없다.
4층에서 던졌는데 달걀이 안 깨졌다면, 5층에 f가 있을 수 있다.
3층에서 던졌는데 달걀이 안 깨졌다면, 4~5층에 f가 있을 수 있다.
2층에서 던졌는데 달걀이 안 깨졌다면, 3~5층에 f가 있을 수 있다.
1층에서 던졌는데 달걀이 안 깨졌다면, 2~5층에 f가 있을 수 있다.
이것을 수식으로 나타내면 아래와 같다.
- drop(eggs, floors - current floors) : 달걀이 안 깨졌고 내 층수 위로 확인 필요
이런 방식으로 계속 이어 나가다 보면 각 층을 Start Point로 했을 경우 가장 Max가 되는 Moves횟수를 찾을 수 있다.
다시 말하지만 모든 경우를 확실히 찾을 수 있다는 Guaranty 가 되어야 하기 때문이다.

위의 그림을 보면 4층이 Start Point일때 안깨졌다면 5층으로 1번 move 4에서 깨졌다면 1~3번 3번 move가 필요하기 때문에 이때 move의 횟수는 Max값인 4 (3+1) 이 답이 되는 것이다.

각 층을 Start Point로 했을 때 나오는 경우의 수는 아래와 같이 된다.
1층 3번, 2층 3번, 3층 3번, 4층 4번 5층 4번이다.
이중에 가장 짧은 값인 3을 선택하면 답이 된다.
var superEggDrop = function(k, n) {
let dp = new Array(k+1).fill(0).map(_ => new Array(n+1).fill(-1)); //[egg,floor]
let result = helper(k, n);
return result;
function helper(eggs, floors) {
if(eggs === 1) return dp[eggs][floors] = floors;
if(floors === 1) return dp[eggs][floors] = 1;
if(floors === 0) return dp[eggs][floors] = 0;
if(0 <= dp[eggs][floors]) return dp[eggs][floors];
let min = Number.MAX_SAFE_INTEGER;
let minEggs = 0;
let minFloors = 0;
for (let i = 1; i <= floors; i++) {
min = Math.min(min,Math.max(helper(eggs, floors - i)+1,helper(eggs - 1, i-1)+1)); //not broken, broken
}
return dp[eggs][floors] = min;
}
};코드는 위와 같다.
Time Complexity는 달걀을 한번을 살리고 한번은 깨는 방식으로 $ N^2 $을 선택하고 모든 층을 순회 함으로 $$ O(KN^2) $$ 이 된다.
$ N^2 $ 이 헷깔릴 수가 있어서 조금더 내용을 남기자면, 첫 move에 N개의 층을 선택하고 2번째 move는 선택된 층을 제외한 N-1개 층을 조회하기 때문이다. 즉 N + (N-1) + (N-2) ... 1 이 되어서 $ N^2 $ 이 된다.
그런데 이 경우는 TLE가 발생하게 된다.
그럼 어떻게 하면 최적화가 가능할까?
아래의 예를 한번 생각해 보자.

깨질때와 안깨질 때의 공식을 보면 상호 반 비례한다는 것을 알 수 있다.
하나는 Floors가 높을 수록 Moves가 늘어나고 다른 하나는 Floors가 낮을 수록 Move 수가 늘어나게 된다.
이것을 그래프로 보면 아래와 같다.

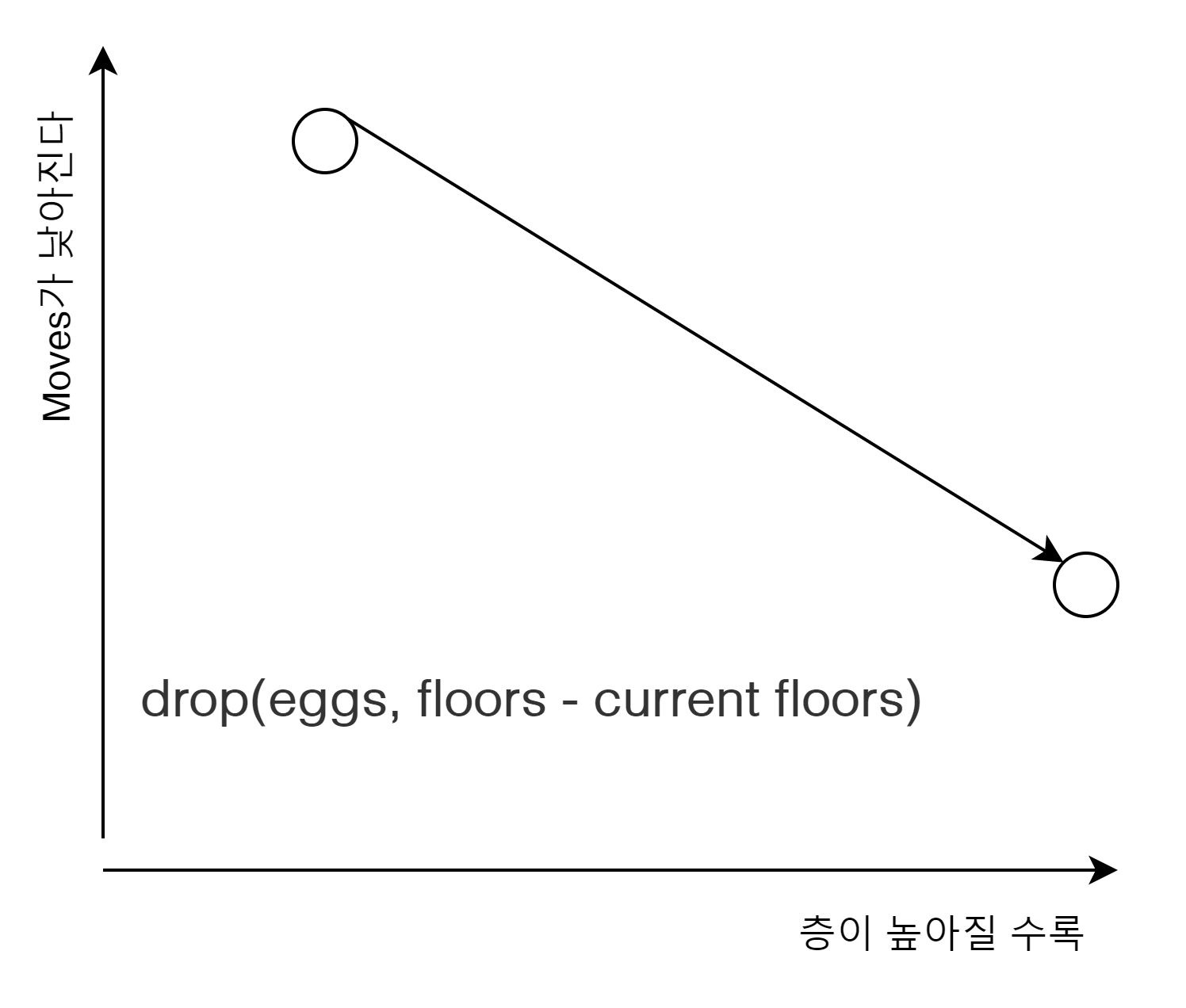
이것을 하나로 합쳐 보자.

층수가 매우 낮은 상태일 때는 drop(eggs - 1, floors - 1)의 Moves가 drop(eggs, floors - current floors)의 Moves가 현저히 낮지만 우리는 Max의 값을 선택해야 함으로 Movew가 높은 drop(eggs, floors - current floors)을 선택하게 된다.
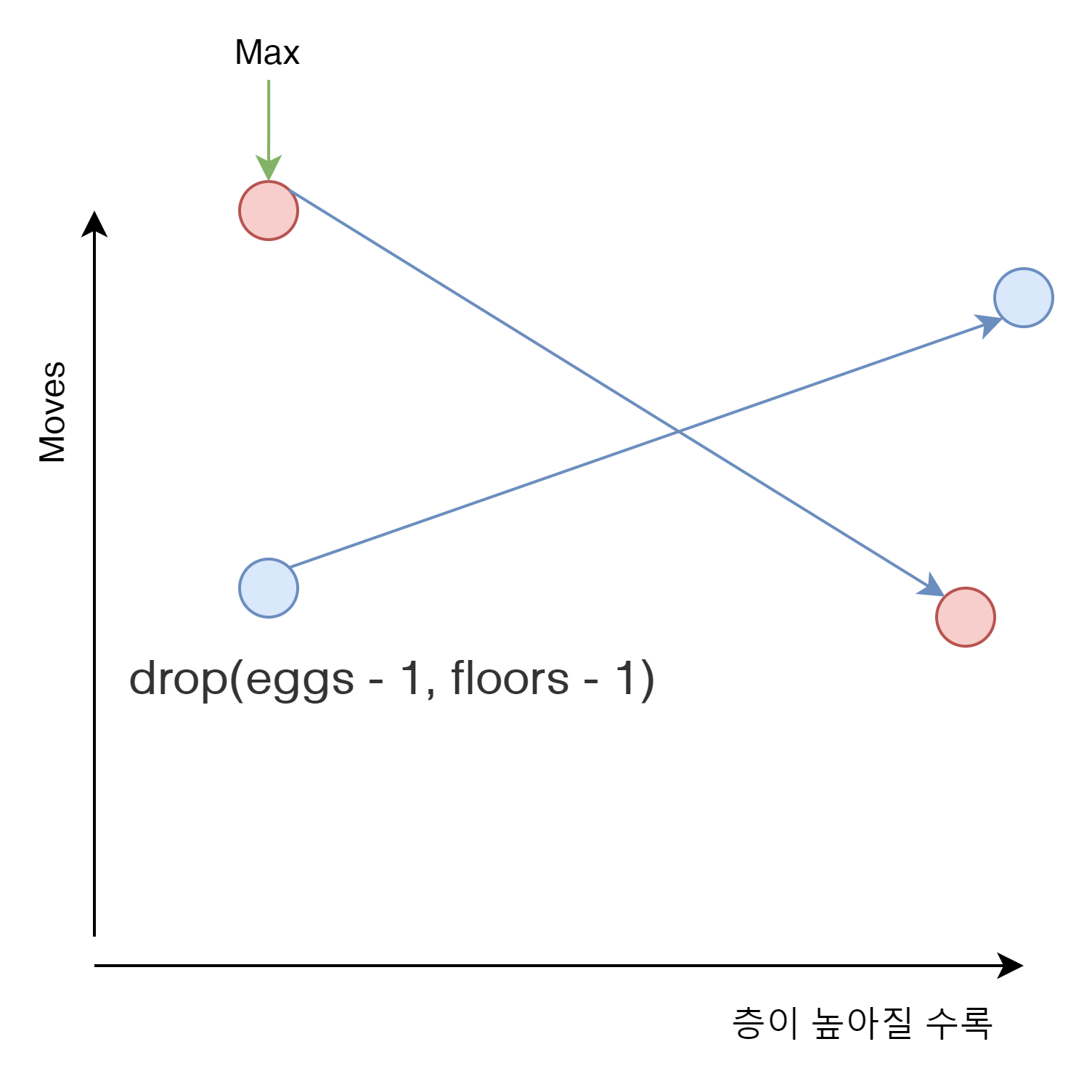
그럼 층이 현저히 높다면?

drop(eggs - 1, floors - 1)의 Moves가 가장 높은 값을 갖게 된다. 그럼 Max의 값이 가장 낮아지는 시점은 어디인가?

바로 두선이 만나는 어느 한 지점이 되게 된다.
- 만난다는 의미는 두개의 Moves가 같다는 의미이다.
- Moves가 한쪽이 더 높으면 높은 쪽을 낮추고 낮은 쪽을 올려야한다.
이것을 Binary Search를 통해서 처리가 가능하다.
var superEggDrop = function(k, n) {
let dp = new Array(k+1).fill(0).map(_ => new Array(n+1).fill(-1)); //[egg,floor]
let result = helper(k, n);
return result;
function helper(eggs, floors) {
if(eggs === 1) return dp[eggs][floors] = floors;
if(floors === 1) return dp[eggs][floors] = 1;
if(floors === 0) return dp[eggs][floors] = 0;
if(0 <= dp[eggs][floors]) return dp[eggs][floors];
let result = floors;
let bottom = 1;
let top = floors;
while (bottom < top) {
let mid = bottom + Math.floor((top - bottom) / 2);
let topSteps = helper(eggs, floors - mid) + 1; // not broken -> 위로 올라가야한다
let bottomSteps = helper(eggs - 1, mid - 1) + 1; //broken -> 밑으로 내려가야 한다
result = Math.min(result, Math.max(topSteps, bottomSteps));
if(topSteps === bottomSteps) { // 둘이 같기 때문에 어느쪽으로도 움직일 필요 없음
break;
}
if(topSteps > bottomSteps){ //worst case를 찾아야 하기 때문에 range를 다시 잡는다.
bottom = mid + 1; //bottom을 위로 올린다
} else {
top = mid; //top이 mid가 된다. 아래로 절반을 내린다.
}
}
return dp[eggs][floors] = result;
}
};적당한 층을 binary search로 조회함으로 모든 층을 순회할 필요가 없다.
$$ O(KNLogN) $$
첫번째 Move부터 적절한 층을 Binary Search 방식으로 접점을 찾아가기 때문에 N LogN이 된다
이것이 Time complexity가 된다.
Bottom Up
Bottom up은 여러가지 접근 방법이 있는데, 가장 쉬운 것은 위의 binary Search를 DP화 한것이다.
우선 달걀 3개에 5층 Floor의 경우를 생각해 보자.
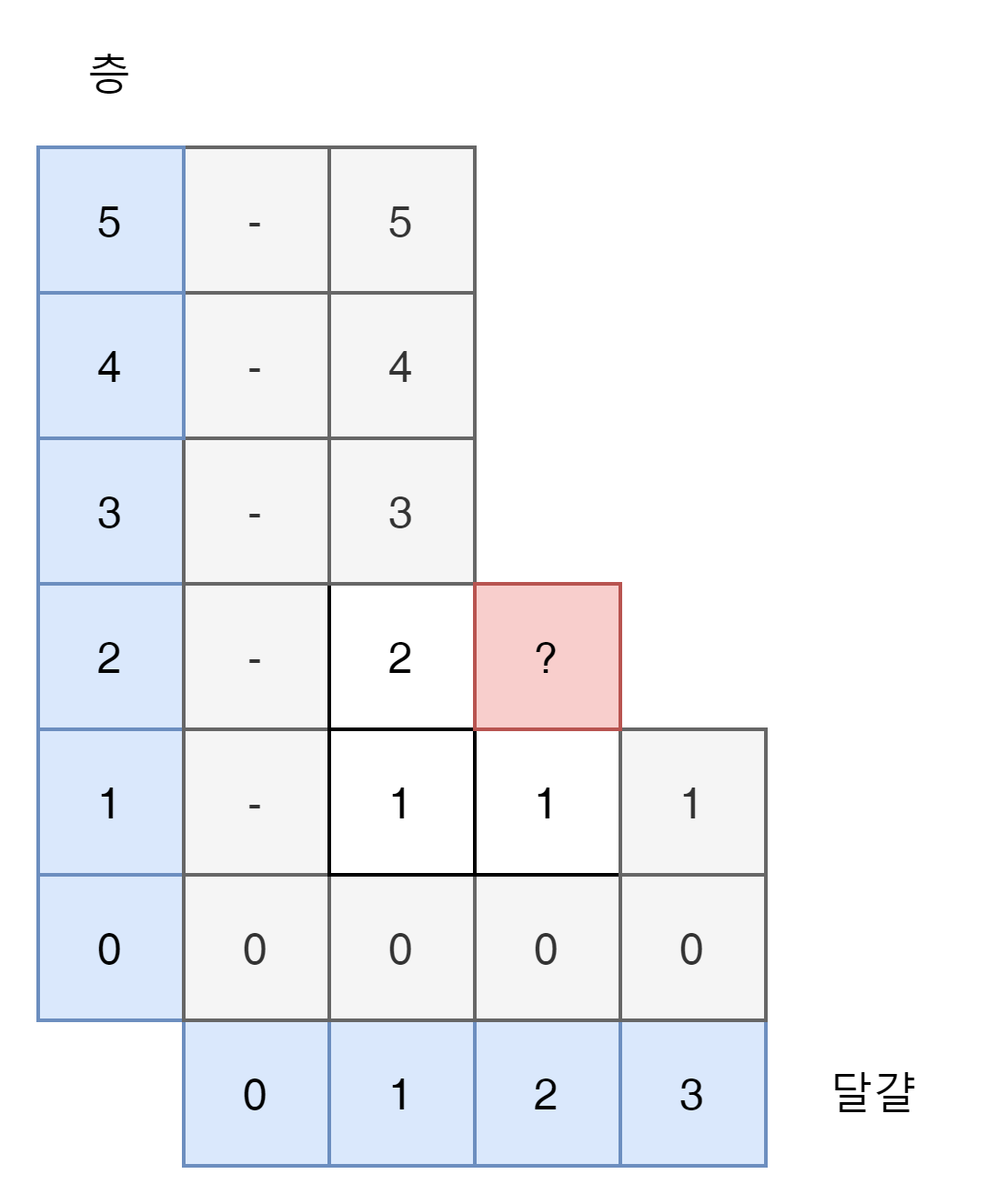
상위 이미지를 보면 알겠지만 달걀이 하나일때와 층이 1층일때의 Moves 수는 확정된다.
- 달걀이 하나일때 욺직이는 Move 수는 층수와 동일하다
- 층이 하나일때는 달걀의 수가 1이상이면 1 Move 이다
그러면 달걀 2개에 2층은 어떨까?
달걀 2개의 2층일때 Max Move는
- Min(각층 Max(drop(eggs, floors -current floors), drop(eggs-1, floors -1) +1))
이다.
drop(1,1)
drop(2,1)
에서 부터 깨진 경우와 안깨진 경우의 Min Move 수를 찾으면 되는데, 이미 Binary Search를 통해서 찾는 부분은 이전에 배웠다.
첫번째 center는 $ 1 = \frac{2-1}{2} + 1 $ 이 된다.
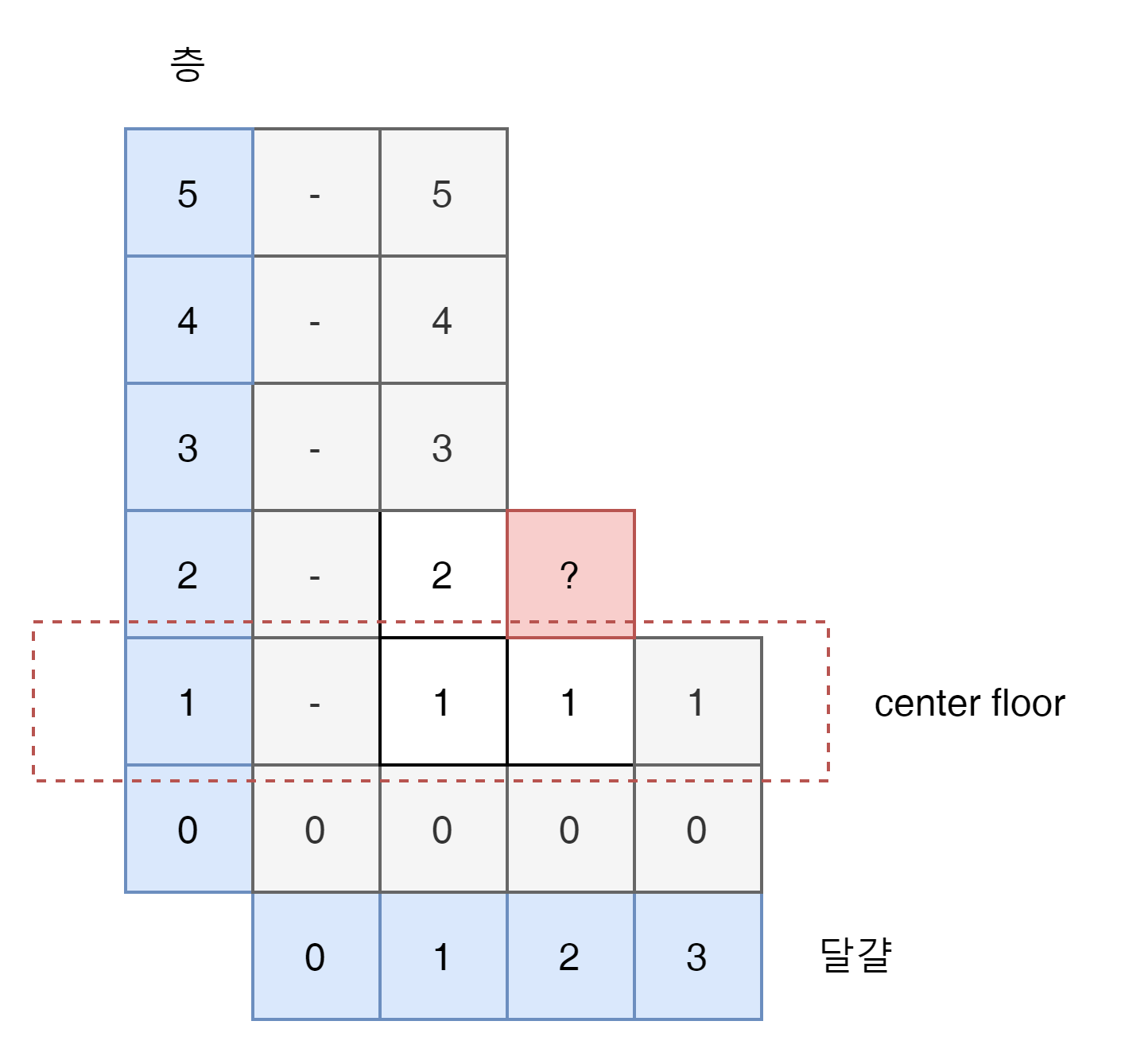
달걀은 2이고 center가 1일때 깨진 경우는 drop(1,0) + 1, 안깨진 경우는 drop(2, 1) + 1이 된다.
깨진 경우가 1, 안깨진 경우는 2가 되고 안깨진 경우가 더 높은 수 임으로 위로올라 가야해서 bottom을 center+1로 만들어 준다.
이 경우 bottom과 top의 값이 같아 짐으로 마지막으로 Max였던 2가 답이 된다.
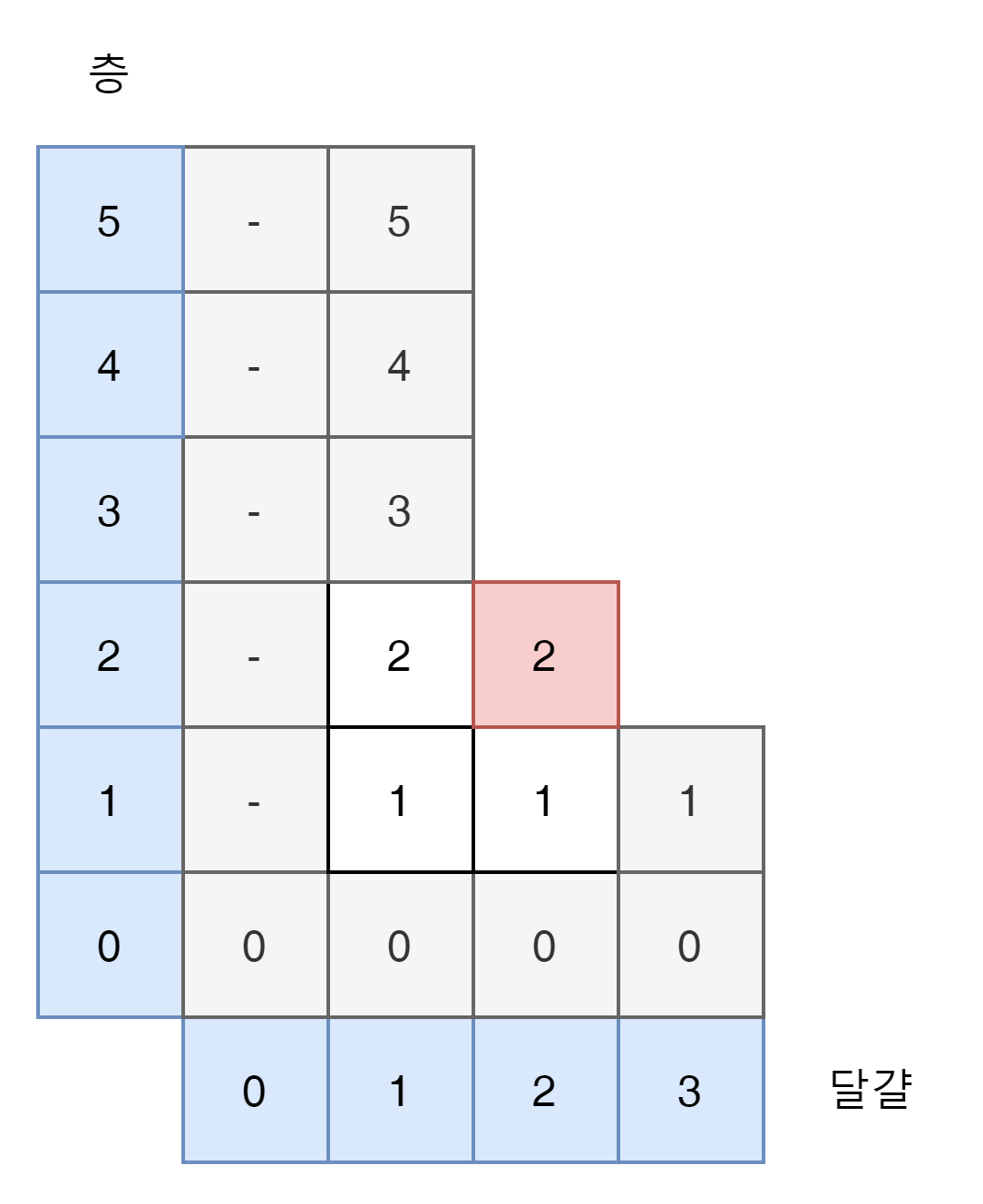
drop(2,3)을 확인해 보자.

center는 2가 된다. 깨진 경우 drop(1,1) 안깨진 경우 drop(2, 1) 을 비교하자. 둘다 Max가 1임으로 +1 move를 해서 2가 답이 된다.
drop(2,4)는

center가 2이고
drop(1,1), drop(2,2)를 비교하면 2, 3이 된다.
여기서 Max는 3이된다.
안깨진 경우가 더 큼으로 bottom을 center +1로 올려준다.
center = bottom + (4 - 3)/2 임으로 center는 3이된다.
drop(1,2)와 drop(2, 1)을 비교하면 각각 3, 2가 됨으로 Max는 다시 3이 된다.
깨진쪽이 더 큼으로 top을 center로 옮기게 되면 top과 bottom이 같아져서 Min(Max(3,3)) 이 되어서 답은 3이 된다.
이제 달걀 2개와 5층일 경우이다.
center = bottom + (5 -1)/2 임으로 center는 3이다.

각각 drop(1,2), drop(2,2)가 되고 각각 3, 3이 답이 된다. 같은 값임으로 3이 답이 되고 종료된다.
달걀 3개도 같은 방법으로 처리하면

이 되게 된다.
var superEggDrop = function(k, n) {
let dp = new Array(k + 1).fill(0).map(_ => new Array(n + 1).fill(0));
for (let i = 0; i <= n; i++) {
dp[1][i] = i;
}
for (let i = 1; i <= k; i++) {
dp[i][1] = 1;
}
for (let egg = 2; egg <= k; egg++) {
for (let floor = 2; floor <= n; floor++) {
let bottom = 1;
let top = floor;
let result = n;
while (bottom < top) {
let mid = bottom + Math.floor((top - bottom) / 2);
let topSteps = dp[egg][floor - mid] + 1; // not broken -> 위로 올라가야한다
let bottomSteps = dp[egg-1][mid - 1] + 1; //broken -> 밑으로 내려가야 한다
result = Math.min(result, Math.max(topSteps, bottomSteps));
if(topSteps === bottomSteps) { // 둘이 같기 때문에 어느쪽으로도 움직일 필요 없음
break;
}
if(topSteps > bottomSteps){ //worst case를 찾아야 하기 때문에 range를 다시 잡는다.
bottom = mid + 1; //bottom을 위로 올린다
} else {
top = mid; //top이 mid가 된다. 아래로 절반을 내린다.
}
}
dp[egg][floor] = result;
}
}
// console.log(dp);
return dp[k][n];
}전 층을 다 순회 함으로
$$ O(KNLogN) $$
는 동일 하다.
여기서 성능을 $ O(KN) $ 까지도 늘릴 수 있는데, 이해가 어려워서 이쯤에서 본 문제는 끝을 내고자 한다.
몇개 이해하는데 도움이 되었던 글을 여기 붙인다.
https://github.com/just4once/leetcode/blob/master/leetcode/binary-search/887-super-egg-drop.md
https://brilliant.org/wiki/egg-dropping/
https://www.youtube.com/watch?v=iOaRjDT0vjc
https://www.youtube.com/watch?v=NGtt7GJ1uiM
'Problem Solving' 카테고리의 다른 글
| Confirmation Rate (0) | 2021.08.02 |
|---|---|
| 2진수 최 좌측 1자리 찾기 (0) | 2021.08.02 |
| Valid Perfect Square (Newton's Method) (0) | 2021.07.27 |
| 132 Pattern (0) | 2021.07.25 |
| Minimum Number of Increments on Subarrays to Form a Target Array (0) | 2021.07.24 |
