어떤 값의 분류가 잘 되어있을 확률을 나타낸다.
예를 들자면 아래와 같은 그래프가 있다고 보자.

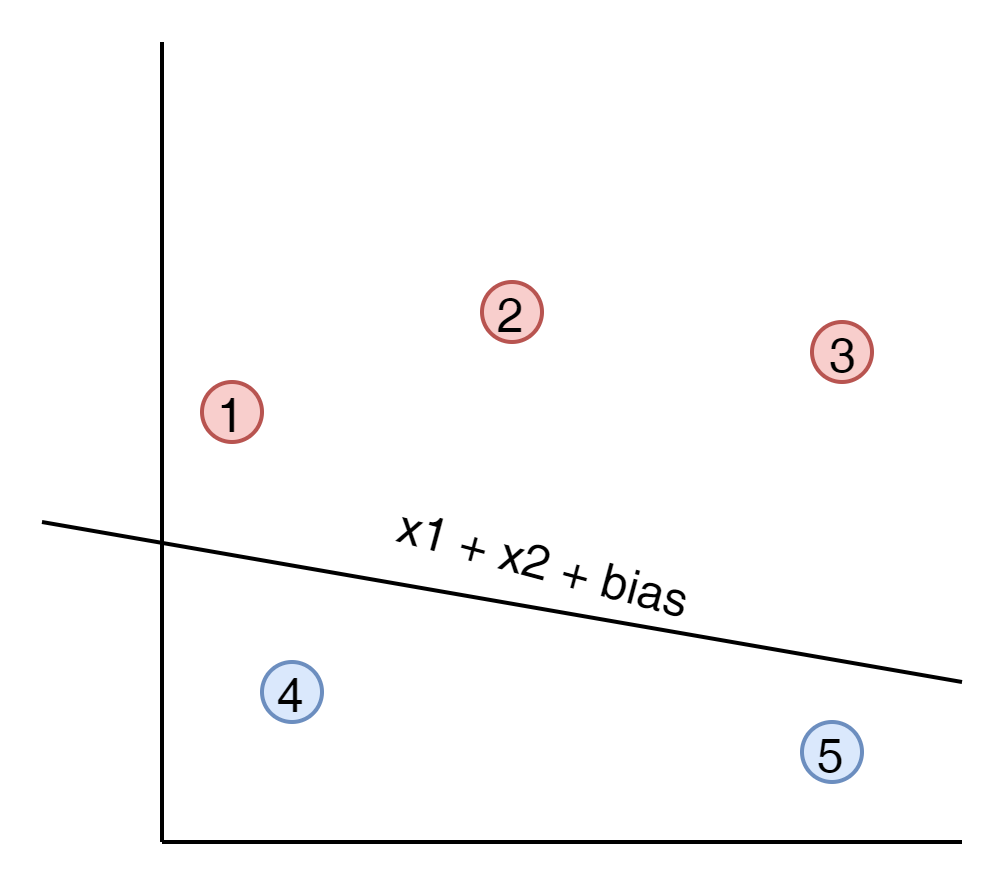
분리된 선을 기준으로 아래쪽을 파란영역 위 쪽을 붉은 영역이라고 보면
아래는 2개의 Points가 있고 상단에는 3개의 Points가 있다.
이 영역을 다음과 같이 확률로 계산이 가능하다.
우선 하단 파란영역을 보자.

위에 1번 point가 파랑일 확률은? 0.2라고 생각하고, 2번 Point가 파랑일 확률은 0.8로 높을 것이다.
마찬가지로 상단의 3개 points도 각각 0.9, 0.8, 0.1 이라고 생각해 보자.
이 값들을 모두 곱한 값은 아래와 같게 된다.
$$ 0.2 * 0.8 * 0.9 * 0.8 * 0.1 = 0.01152 $$
만약에 모든 포인트가 잘 분류 되었다고 생각해 보자.
상단 points가 빨강일 확률은 0.9, 0.9, 0.8 이라고 상상해 볼 수 있다. 잘 분리 되었기 때문이다.
마찬가지로 파랑이 확률도 0.9, 0.8 로 높아질 것이다. 이것을 다시 곱해보자.
$$ 0.9 * 0.9 * 0.8 * 0.9 * 0.8 = 0.46656 $$
잘 분류 되었을 경우의 확률 곱이 매우 높아진 것을 알수 있다. 이것을 Maximizing Probabilities 라고 부른다.
그런데 문제가 하나 있다. 만약에 해당 Points가 너무 많다면 어떻게 될까?
각 포인트별 확률임으로 0과 1사이의 값이 Points의 갯수 만큼 많게 계산이 될 것이고 이는
floating연산이 굉장히 많은 소수로 이루어진 값으로 만들어지게 된다.
이부분을 해결하기 위해서 각 확률을 log에 대입하게 된다.
곱셈을 쉽게 하는 tool로써 log를 사용한 것이지 다른 의미가 있지는 않다.
곱셈을 덧샘으로 바꿔주는 마법을 log가 만들기 때문이다.
밑은 계산이 편하게 e로 한다. 물론 10으로 해도 상관은 없다. 결과의 높고 낮음을 보기 위한 목적이기 때문이다.
$$ log_e 0.9 + log_e 0.9 + log_e 0.8 + log_e 0.9 + log_e 0.8 = -0.762368649602 $$
그런데 음수가 나오는 것을 볼 수 있다. 이유는

log는 0에서 1사이의 입력이 들어온 값이 마이너스로 나이기 때문이다. 이를 양수로 만들기 위해서 전체를 빼기로 만들어 주자.
$$ -log_e 0.9 - log_e 0.9 - log_e 0.8 - log_e 0.9 - log_e 0.8 = 0.762368649602 $$
이때 주의해야 할것은 음수로 변경했음으로 낮은 값의 결과값이 높은 결과값 보다 좋은 결과를 갖어 온다는 것이다.
이것을
Cross Entropy라고 부르며
- 낮은 값이 우수한 모델이다
상기 내용을 잘 생각해 보면 결과 적으로 Label된 목표 값과 동일한 경우 가장 낮은 Cross Entropy를 얻을 수 있었다.
이것을 수학적으로 나타내면 아래와 같다.
$$ CrossEntropy() = - \sum_{i=1}^n y_i*ln(p_i) + (1-y_i)*ln(1-p_i) $$
여기서 y_i는 목표 label이 맞는가를 나타낸다. 즉 1이라면 blue가 blue일 확률이 높기 때문에 확률 자체를 사용하고, 0이라면 blue가 blue가 아닐 확률이 높기 때문에 1 - blue일 확률을 뺀값을 sum해주면 된다.
코드로는 아래와 같다.
import math
def cross_entropy(Y,P):
result = 0;
for i in range(0,len(Y)):
if Y[i] == 1:
result -= math.log(P[i])
elif Y[i] == 0 :
result -= math.log(1 - P[i])
return result
y = np.array([1,1,0]);
p = np.array([0.8,0.7,0.1]);
print(cross_entropy(y,p));
만약에 2개의 분류가 아닌 3개의 분류는 어떻게 계산 해야 할까?

과일이 3가지가 있고 첫번째에는 사과를 두번째 세번째는 파인이 있다는 것을 알고 있다고 하자 Maximizing Probabilities는
$$ 0.7 * 0.3 * 0.4 = 0.084 $$
가 된다. 이것을 Cross Entropy로 바꾸어 보자
$$ -log_e 0.7 - log_e 0.3 - log_2 0.4 = 2.48 $$
이 된다.
이걸 수식으로 표현 하면 아래와 같이 나타낼 수 있다.
$$ CrossEntropy() = - \sum_{i=1}^n \sum_{j=1}^m j_{ij}*ln(p_{ij}) $$
여기에서 j는 사과, 바나나, 파인애플의 순서를 뜻하고 i는 각 라운드를 표시한다.
즉 i가 1이고 사과 j가 1이라면 0.7이 되게 된다.
'AI' 카테고리의 다른 글
| Gradient Descent (0) | 2021.07.18 |
|---|---|
| Error Function (0) | 2021.07.18 |
| Softmax function (0) | 2021.07.17 |
| Sigmoid Function (0) | 2021.07.17 |
| Perceptron Algorithm 코드 (0) | 2021.07.17 |
