경사 하강법에 대해서 알아 보고자 한다.
기본 적인 Error Function의 구조는 아래 링크와 같다.
2021.07.17 - [AI] - Error Function
$$ ErrorFunction() = - \frac{1}{n} \sum_{i=1}^n y_i*ln(\sigma(Wx_i + b)) + (1-y_i)*ln(1-\sigma(Wx_i + b)) $$
이것을 3차원의 형태로 그려보면 아래와 같이 표현 할 수 있다.
아래 E 또는 Error 가 Error Function의 계산 결과 이다.
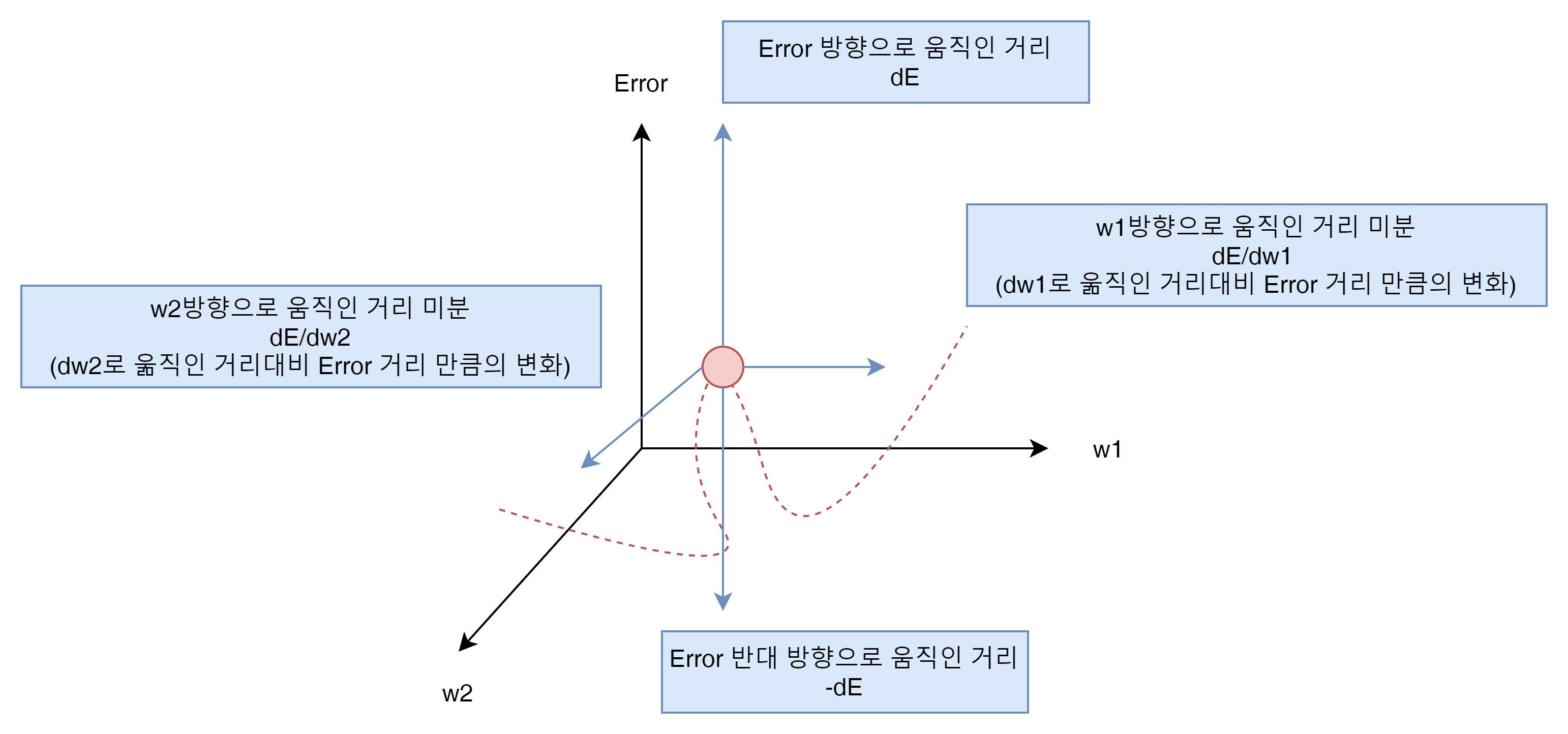
즉, w1의 변화량은 Error function의 결과 값에 어느 정도의 변화를 만들어 내는가?
w2의 변화량은 Error function의 결과값에 어떤 변화를 만들어 내는가?
이것을 표현한 내용이라고 생각하면 된다.
그리고 궁극적인 목표는 Error를 최소화 하는 것임으로 -dE 를 w1과 w2의 변화로 극소로 만들어 내는 것을 목표로 한다.
이것을 오차함수의 기울기라는 표현 방식으로 나타낼 수 있다.
우선 최초 예측값을 나타내는 수식을 보자.
$$ \hat{y} = \sigma(Wx + b) $$
이 수식은 아직 W와 b를 update 하기 이전의 수식임으로 예측률이 별로 좋지 않다.
이 수식에 W wehight가 N개 있다고 생각하면 아래와 같이 수식으로 나타낼 수 있다.
$$ \hat{y} = \sigma(W_1x_1 + ... + W_nx_n + b) $$
위 그림에서는 W가 2개가 있다.
이 예측 값을 오차함수의 기울기로 vector 좌표를 만들어 보고자 한다.
그림으로 나타내면 아래와 같다.

w1과 w2의 위치를 통해서 Error라는 위치가 결정 된다는 것을 알것이다.
즉, $ Error 좌표 = Error Function(w1,w2,bias) $ 로 표현 가능하다.
만약에 w1을 조금 움직이고 w2를 조금 움직인다면 우리는 이 변화량이 Error 좌표에 어느정도 변화를 주는 가를 확인 할 수있다.
이것을 수식으로 아래와 같이 나타낸다.
$$ \nabla{E} = (\partial{E}/\partial{w_1}, \partial{E}/\partial{w_2}, \partial{E}/\partial{b}) $$
즉 weight와 bias의 변화로 인해서 $ \nabla{E} $ 가 얼마나 변화 하는지를 확인 하면 된다.
앞서 언급했지만 dE는 마이너스로 가는 것이 좋은 것이다.
이중에 다음 수식 하나만을 생각해 보자.
$$ \partial{E}/\partial{w_1} $$
$ w_1 $의 변화량으로 $ E $ 의 변화량을 미분한 값이다. 이를 통해서 $ w_1 $ 을 아래와 같이 재 정의 할 수 있다.
$$ {w'}_i = w_i - \alpha * \partial{E} / \partial{w_i} $$
여기에서 $ \alpha $ 는 learning rage로 급격한 변화를 방지하는 용도로 사용된다. 0.1, 0.2 등 원하는 값을 넣어 주면 된다. bias도 같은 방법으로 처리해 주면 된다.
$$ b' = b - \alpha * \partial{E} / \partial{b} $$
이제 수식을 편리하게 만들기 위해서 아래 두 가지를 간단한 수식으로의 변화가 필요하다.
- $ w_i $ 로 E를 미분하는 것 $ \partial{E} / \partial{w_i} $
- bias로 E를 미분하는 것 $ \partial{E} / \partial{b} $
이것을 수학적인 증명을 통해 아래와 같이 간단하게 만들 수 있다. (수학증명은... pass)
$$ \partial{E} / \partial{w_i} = -(y - \hat{y}) * x_i $$
$$ \partial{E} / \partial{b} = -(y - \hat{y}) $$
이 두가지를 바탕으로 오차함수 기울기의 delta는
$$ \nabla{E} = -(y-\hat{y})(x_1,...,x_n,1) $$
이 되게 된다.
그럼 좋은 예측 $ \hat{y} $는 무었일까?
- 예측된 값이 목표한 label에 가까와질 수록 기울기는 줄어든다.
- 예측된 값이 목표 label과 멀어질 수록 기울기는 늘어난다.
기울기가 클수록 좌표의 위치를 크게 변경하게 된다는 것을 알 수 있다.
이제 마지막으로 앞서 나온 결과를 바탕으로 다음 update 될 weight를 얻어오는 공식을 간단히 민들어 보자.
$$ {w'}_i = w_i - \alpha * \partial{E} / \partial{w_i} $$
이 기본 공식에서 $ \partial{E} / \partial{w_i} $ 를 간단히 만든 부분으로 교체 하자
$$ {w'}_i = w_i - \alpha * -(y - \hat{y}) * x_i $$
여기에 마이너스를 통합하면,
$$ {w'}_i = w_i + \alpha * (y - \hat{y}) * x_i $$
가 된다. Bias도 동일한 방식으로
$$ b' = b + \alpha * (y - \hat{y}) $$
을 최종 공식으로 도출 가능하다.
최종적으로 Gradient Descent를 만들기 위해 필요한 코드는 다음과 같다.
- Sigmoid activation function
$$\sigma(x) = \frac{1}{1+e^{-x}}$$
- Output (prediction) formula
$$\hat{y} = \sigma(w_1 x_1 + w_2 x_2 + b)$$
- Error function
$$Error(y, \hat{y}) = - y \log(\hat{y}) - (1-y) \log(1-\hat{y})$$
- The function that updates the weights
$$ w_i \longrightarrow w_i + \alpha (y - \hat{y}) x_i$$
$$ b \longrightarrow b + \alpha (y - \hat{y})$$
이것을 코드로 짜면 아래와 같다.
# Activation (sigmoid) function
def sigmoid(x):
return 1 / (1 + np.exp(-x))
# Output (prediction) formula x and weight and bias y hat
def output_formula(features, weights, bias):
return sigmoid(np.dot(features, weights) + bias)
# Error (log-loss) formula
def error_formula(y, output):
return -y * np.log(output) - (1 - y) * np.log(1 - output)
# Gradient descent step
def update_weights(x, y, weights, bias, learnrate, output):
error = y - output
weights += learnrate * error * x
bias += learnrate * error
return weights, bias이 코드를 짤때 주의해야 할 것은 x와 weights의 dimensions는 같아야 한다는 것이다.
이 코드를 바탕으로 Training을 위한 코드는 다음 순서에 따라서 작성 된다.
- epochs(세대)를 몇번 회전할지와 learnrate를 정의 한다.
- x의 Dementions 또는 features의 값에 대응되는 Random weights를 얻는다
- output formula와 sigmoid를 통해서 예측 값을 얻어온다
- x의 갯수만큼 loop를 돌면서 weight와 bias를 업데이트 한다.
- 모든 x를 다 돈 후 최종 결과 예측 값과 error_formula(loss function) 값을 얻는다.
- 다시 1-1번 부터 1-4번까지 epochs 만큼 업데이트 한다.
결과는 아래와 같이 녹색선이 점점 검정선이 될때까지 업데이트 되는 것을 확인 가능하다.
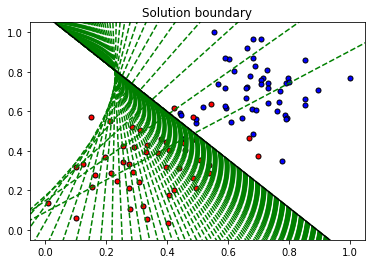
Error의 값도
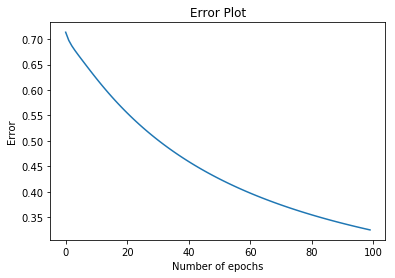
세대를 지날 수록 낮아 지나는 것을 확인 가능하다.
결과적으로
2021.07.17 - [AI] - Perceptron Algorithm 코드
Perceptron과 Gradient Descent은 거의 흡사한 알고리즘이다.
단지 다른게 있다면
- Perceptron은 0과 1의 Label 된 예측값의 차이로 계산을 한다
- Gradient Descent는 0과 1사이의 예측값의 차이로 계산이 된다.
Gradient Descent는 각 점별로 Error 값을 최소화 하기 위해서
- 분류가 잘된 점은 선을 밖으로 밀어내고
- 분류가 잘못된 점은 선을 자신쪽으로 끌어 당기는 역할을 한다.
이것은 분류가 완료 된것처럼 보이지만 epochs가 계속 되는한 계속 이와 같은 행위를 하게 된다.
코드로는 아래와 같다.
np.random.seed(44)
epochs = 100
learnrate = 0.01
def train(features, targets, epochs, learnrate, graph_lines=False):
errors = []
n_records, n_features = features.shape
last_loss = None
weights = np.random.normal(scale=1 / n_features**.5, size=n_features)
bias = 0
for e in range(epochs):
del_w = np.zeros(weights.shape)
for x, y in zip(features, targets):
output = output_formula(x, weights, bias)
error = error_formula(y, output)
weights, bias = update_weights(x, y, weights, bias, learnrate, output)
# Printing out the log-loss error on the training set
out = output_formula(features, weights, bias)
loss = np.mean(error_formula(targets, out))
errors.append(loss)
if e % (epochs / 10) == 0:
print("\n========== Epoch", e,"==========")
if last_loss and last_loss < loss:
print("Train loss: ", loss, " WARNING - Loss Increasing")
else:
print("Train loss: ", loss)
last_loss = loss
predictions = out > 0.5
accuracy = np.mean(predictions == targets)
print("Accuracy: ", accuracy)
if graph_lines and e % (epochs / 100) == 0:
display(-weights[0]/weights[1], -bias/weights[1])
# Plotting the solution boundary
plt.title("Solution boundary")
display(-weights[0]/weights[1], -bias/weights[1], 'black')
# Plotting the data
plot_points(features, targets)
plt.show()
# Plotting the error
plt.title("Error Plot")
plt.xlabel('Number of epochs')
plt.ylabel('Error')
plt.plot(errors)
plt.show()'AI' 카테고리의 다른 글
| Backpropagation (0) | 2021.08.01 |
|---|---|
| Feedforward (0) | 2021.07.18 |
| Error Function (0) | 2021.07.18 |
| Maximizing Probabilities, Cross Entropy (0) | 2021.07.18 |
| Softmax function (0) | 2021.07.17 |
