앞서 Neural Network 의 선형적 계산 방식을 Neural Network로 보자면,
다음과 같은 모습으로 생각할 수 있다.

weight가 각각 2와 3의 그래프가 있고 bias가 -2라고 하면

이런 형태의 그래프를 그릴수 있게 된다.
만약에 한개의 그래프를 더 그려 보면 어떨까?


이런 모습의 그래프를 그릴 수 있다. 이 2가지를 합치면 아래와 같은 모습이 가능하다.

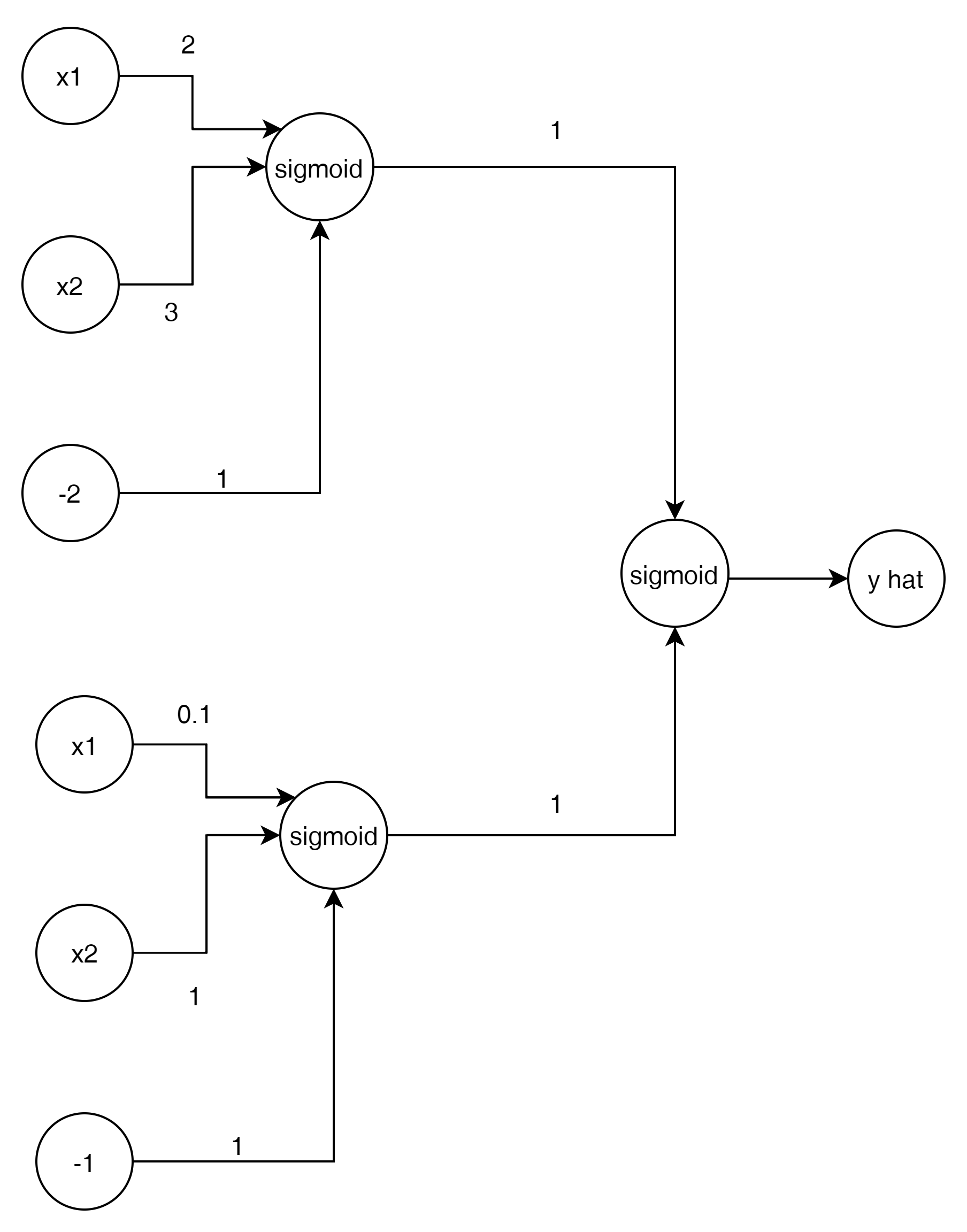
두번째 Layer가 추가 된 것을 볼 수 있다.
즉 2개의 방정식을 하나로 합치는 또다른 방정식을 만든 것이다.
이것 역서 각각 weight를 줄수 있게 된다.

w1에 0.5를 w2에 2 그리고 bias -1을 추가 한것 을 확인 할 수있다.
이 Network를 간단하게 그리면 다음과 같게 된다.
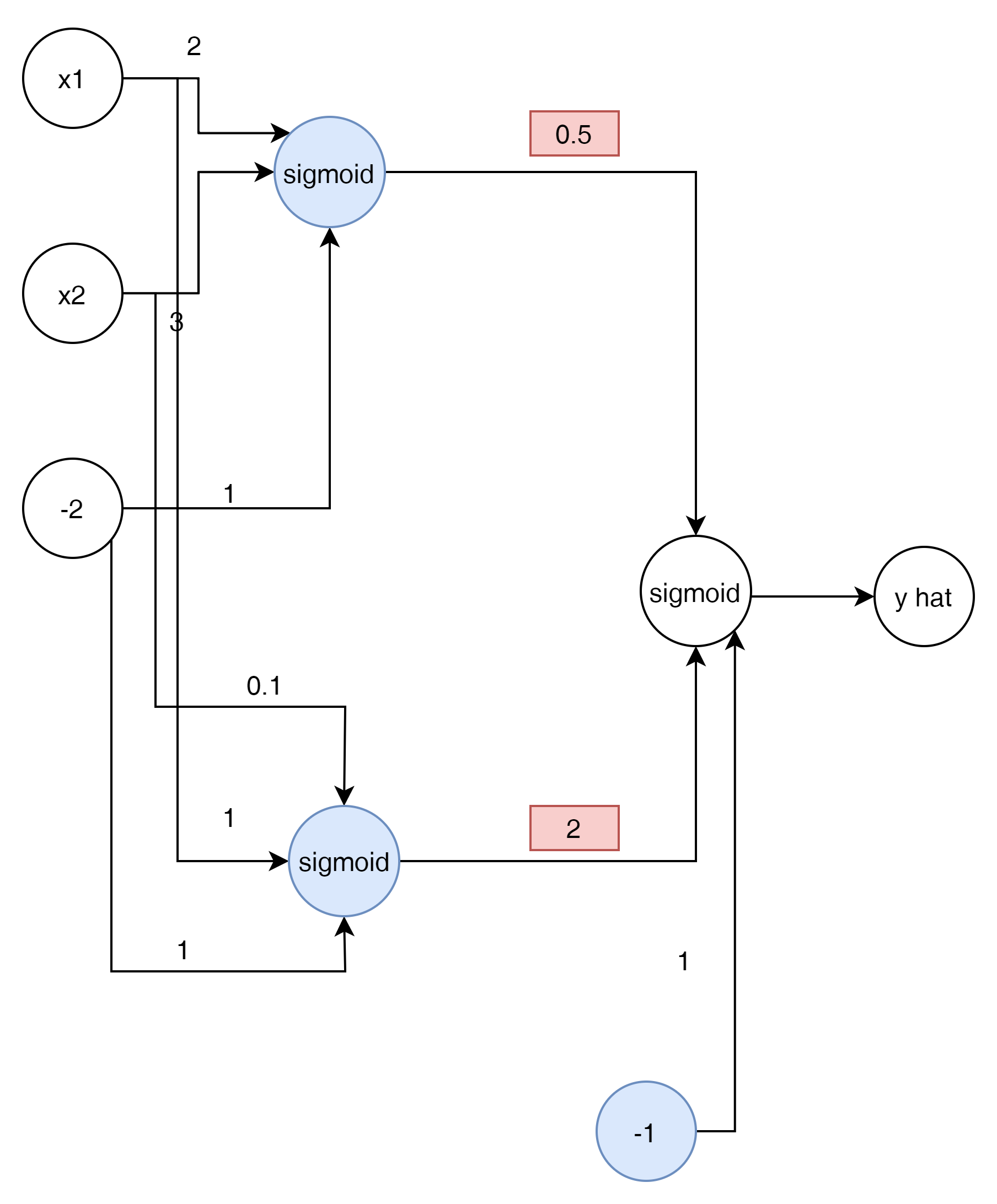
이것을 Matrix로 표현 하면 다음과 같이 표현이 가능하다.
$$ \begin{pmatrix} x1 \\ x2 \\ -2 \end{pmatrix} $$
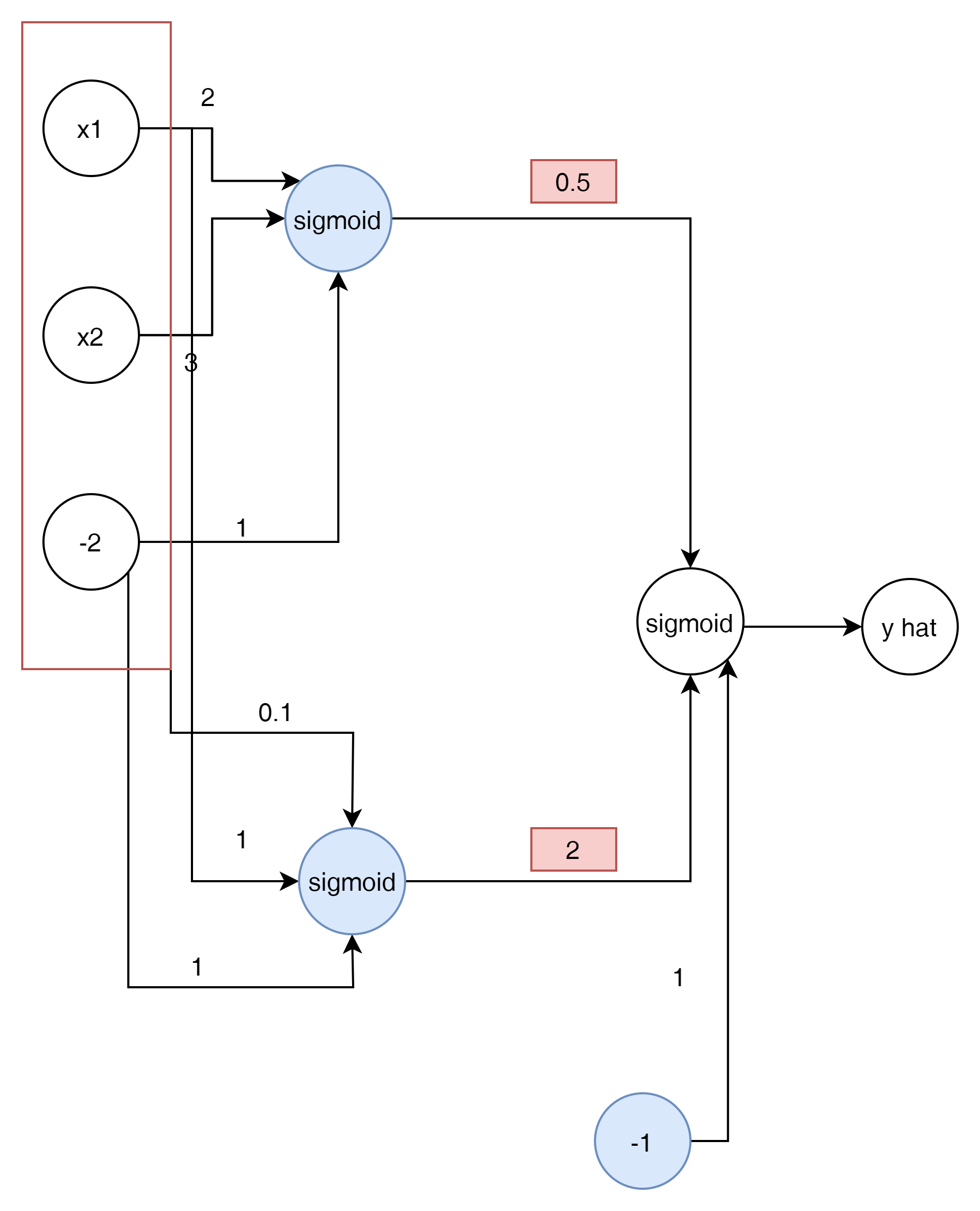
$$ \sigma \begin{pmatrix} w11 && w12 \\ w21 && w22 \\ w31 && w32 \end{pmatrix} \begin{pmatrix} x1 \\ x2 \\ -2 \end{pmatrix} $$

$$ \sigma \begin{pmatrix} {w^(2)}_11 \\ {w^(2)}_w21 \\ {w^(2)}_31 \end{pmatrix} \sigma \begin{pmatrix} w_11 && w_12 \\ w_21 && w_22 \\ w_31 && w_32 \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ -2 \end{pmatrix} $$

$$ \hat{y} = \sigma \begin{pmatrix} {w^{2}}_{11} \\ {w^{2}}_{21} \\ {w^{2}}_{31} \end{pmatrix} \sigma \begin{pmatrix} w_{11} && w_{12} \\ w_{21} && w_{22} \\ w_{31} && w_{32} \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ -2 \end{pmatrix} $$
이렇게 앞선 Layer의 output이 다음 layer의 input이 되는 프로세스를 Feed forward라고 한다.
'AI' 카테고리의 다른 글
| Predicting Student Admissions with Neural Networks (0) | 2021.08.01 |
|---|---|
| Backpropagation (0) | 2021.08.01 |
| Gradient Descent (0) | 2021.07.18 |
| Error Function (0) | 2021.07.18 |
| Maximizing Probabilities, Cross Entropy (0) | 2021.07.18 |
