입학 가능성 예측
여기 있는 코드를 분석하는 내용이다.
여기서 배울 수 있는 것은
- csv 파일 로딩
- matplotlib를 이용한 그래프 표현
- Panda를 이용한 One Hot Coding
- Data 전처리 및 Scaling 변화
- 전처리 Data 및 Test 데이터 분리
- featuers(X)와 결과값(y)의 분리
- 2 layers Network 개발
- Backpropatation
- 정확도 확인
이다.
개인적으로 해당 코드를 보면서 분석한 내용을 붙여 넣는다.
csv 파일 로딩
import pandas as pd
import numpy as np
# Reading the csv file into a pandas DataFrame
data = pd.read_csv('student_data.csv')
# Printing out the first 10 rows of our data
data[:10]csv파일에서 아래와 같은 형상의 데이터를 갖어온다.

admit는 1은 통과 0은 불합격이다.
gre시험 점수, gpa는 학점점수, rank는 Class 수준(1~4)을 분리했다.
matplotlib를 이용한 그래프 표현
# Importing matplotlib
import matplotlib.pyplot as plt
# Function to help us plot
def plot_points(data):
X = np.array(data[["gre","gpa"]])
y = np.array(data["admit"])
admitted = X[np.argwhere(y==1)]
rejected = X[np.argwhere(y==0)]
plt.scatter([s[0][0] for s in rejected], [s[0][1] for s in rejected], s = 25, color = 'red', edgecolor = 'k')
plt.scatter([s[0][0] for s in admitted], [s[0][1] for s in admitted], s = 25, color = 'cyan', edgecolor = 'k')
plt.xlabel('Test (GRE)')
plt.ylabel('Grades (GPA)')
# Plotting the points
plot_points(data)
plt.show()위에서 불러온 데이터를 이용해서,
X는 입력값, Y는 결과값(admit)으로 Array를 나누었다.
이중에 Y가 1인 합격자 Array 입력값과 0인 불합격 Array 입력값을 분리해서,
$ x_1 $ 은 gre축 $ x_2 $ 는 gpa 축으로 분리한 그래프에 합격은 cyan 불합격은 red로 해서 그래프를 그린다.

GRE, GPA의 관계로 인한 학생들의 합불 현황을 볼 수 있다.
# Separating the ranks
data_rank1 = data[data["rank"]==1]
data_rank2 = data[data["rank"]==2]
data_rank3 = data[data["rank"]==3]
data_rank4 = data[data["rank"]==4]
# Plotting the graphs
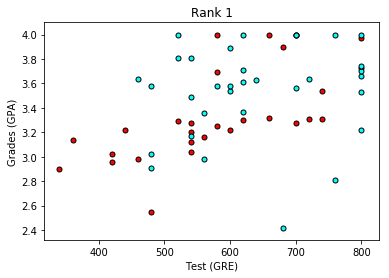
plot_points(data_rank1)
plt.title("Rank 1")
plt.show()
plot_points(data_rank2)
plt.title("Rank 2")
plt.show()
plot_points(data_rank3)
plt.title("Rank 3")
plt.show()
plot_points(data_rank4)
plt.title("Rank 4")
plt.show()마지막으로 rank에 따른 Data 분산을 확인 할 수 있도록
입력되는 데이터를 Rank 값에 따른 분리를 통해서 그래프로 확인 가능 하도록 한다.



Panda를 이용한 One Hot Encoding
One Hot Encoding은 주어진 값이 0또는 1과 같이 이분화 되지 않고 여러개의 의미를 갖을 수 있을 때 활용 되는 방법이다.

여기에서는 Rank를 이용해서 One Hot Encoding을 통해서 표현하는 방법을 코드로 보여준다.
# TODO: Make dummy variables for rank
one_hot_data = pd.concat([data, pd.get_dummies(data['rank'], prefix='rank')], axis=1)
# TODO: Drop the previous rank column
one_hot_data = one_hot_data.drop('rank',axis=1)
# Print the first 10 rows of our data
one_hot_data[:10]Panda에 있는 get_dummies 라고하는 API를 사용 하였다.
https://pandas.pydata.org/docs/reference/api/pandas.get_dummies.html
Rank로 분리한 데이터를 기존 데이터에 붙여 넣고, 기존 데이터 중 더이상 필요없는 rank 필드를 삭제한 코드이다.

Data 전처리 및 Scaling 변화
입력되는 데이터는 일반적으로 0에서 1사이의 값으로 표현될때 계산하기 편리하다.
gre와 gpa는 1이상의 값을 갖고 있음으로 해당 값들이 0고 1사이에 존재 할 수 있도록 데이터를 변환 시켜준다.
# Making a copy of our data
processed_data = one_hot_data[:]
# TODO: Scale the columns
processed_data["gre"] = processed_data["gre"] / 800
processed_data["gpa"] = processed_data["gre"] / 4.0
# Printing the first 10 rows of our procesed data
processed_data[:10]
Training Data 및 Test 데이터 분리
주어진 데이터의 90%를 Training용으로 사용하고, Test로 사용하기 위한 10% 데이터를 분리해야 한다.
sample = np.random.choice(processed_data.index, size=int(len(processed_data)*0.9), replace=False)
train_data, test_data = processed_data.iloc[sample], processed_data.drop(sample)
print("Number of training samples is", len(train_data))
print("Number of testing samples is", len(test_data))
print(train_data[:10])
print(test_data[:10])numpy에 있는 random.choice를 사용해서 가능하다.
https://numpy.org/doc/stable/reference/random/generated/numpy.random.choice.html
Pandas의 Dataframe iloc를 이용해서 train_data와 test data를 분리하자.
https://pandas.pydata.org/pandas-docs/stable/reference/api/pandas.DataFrame.iloc.html

featuers(X)와 결과값(y)의 분리
이제 x의 값으로 input해야하는 값과 예측 결과값과 비교해야하는 결과값 y을 분리해 줘야한다.
admit이 y 값임으로 y와 다른 값들을 분리해 주면 된다.
features = train_data.drop('admit', axis=1)
targets = train_data['admit']
features_test = test_data.drop('admit', axis=1)
targets_test = test_data['admit']
print(features[:10])
print(targets[:10])dataframe의 drop을 사용하면 된다.

2 layers Network 개발
sigmoid 함수 개발 (Activation)
2021.07.17 - [AI] - Sigmoid Function
def sigmoid(x):
return 1 / (1 + np.exp(-x))sigmoid 미분
def sigmoid_prime(x):
return sigmoid(x) * (1-sigmoid(x))
Error Function (2차원)
2021.07.17 - [AI] - Error Function
def error_formula(y, output):
return - y*np.log(output) - (1 - y) * np.log(1-output)
Back Propagation을 위한 Vector 미분
2021.07.31 - [AI] - Backpropagation
def error_term_formula(x, y, output):
return (y-output) * sigmoid_prime(x) * x그런데 갑작이 위의 공식은 어디에서 나온걸까?
http://www.cs.cornell.edu/courses/cs5740/2016sp/resources/backprop.pdf
이 문서의 5page 6. Derivation을 보면

을 볼수 있다.
이 공식이 사용된게 위의 error term formula이다.
나름 이해해 보려고 노력하긴 했는데, 잘 되진 않았다.
여기서 tj는 y와 같고 yj는 $ \hat{y} $이다. $ y_k $ 는 x를 가르킨다고 생각하면 된다.
기본적으로 $ \hat{y} $ 은 sigmoid를 사용함으로 sigmoid 미분은 아래의 공식을 만족시킨다.
$$ \hat{y} * (1 - \hat{y}) $$
Backpropatation
1000번의 training을 하고 learningrate는 0.5 - hyperparameters는 Trainning 중 변화하지 않음
# Neural Network hyperparameters
epochs = 1000
learnrate = 0.5위에서 전처리 되었던 데이터를 Neural Network에 넣어 보자.
features, targets, ephochs는 1000, learnrate는 0.5
# Training function
def train_nn(features, targets, epochs, learnrate):
# Use to same seed to make debugging easier
np.random.seed(42)
n_records, n_features = features.shape
last_loss = None
# Initialize weights
weights = np.random.normal(scale=1 / n_features**.5, size=n_features)
for e in range(epochs):
del_w = np.zeros(weights.shape)
for x, y in zip(features.values, targets):
# Loop through all records, x is the input, y is the target
# Activation of the output unit
# Notice we multiply the inputs and the weights here
# rather than storing h as a separate variable
output = sigmoid(np.dot(x, weights))
# The error, the target minus the network output
error = error_formula(y, output)
# The error term
error_term = error_term_formula(x, y, output)
# The gradient descent step, the error times the gradient times the inputs
del_w += error_term * x
# Update the weights here. The learning rate times the
# change in weights, divided by the number of records to average
weights += learnrate * del_w / n_records
# Printing out the mean square error on the training set
if e % (epochs / 10) == 0:
out = sigmoid(np.dot(features, weights))
loss = np.mean((out - targets) ** 2)
print("Epoch:", e)
if last_loss and last_loss < loss:
print("Train loss: ", loss, " WARNING - Loss Increasing")
else:
print("Train loss: ", loss)
last_loss = loss
print("=========")
print("Finished training!")
return weights
weights = train_nn(features, targets, epochs, learnrate)위의 코드를 아래와 같이 분석해 보았다.
# Initialize weights
weights = np.random.normal(scale=1 / n_features**.5, size=n_features)
x의 features는 6개이다. 이 6개의 x값에 weight를 곱해야 하는데 초기 weights를 random하게 잡는다.
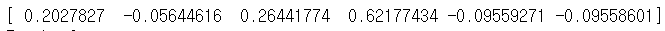
이렇게 gre는 0.2027827이라는 weight가 주어졌음으로 아래와 같이 표시가 가능하다.
$$ y = 0.8 * 0.2027 + 0.2 * -0.056 + 0 * 0.2644.. + 0 * 0.621... + 1 * -0.095... + 0 * -0.0955.. $$
for x, y in zip(features.values, targets):
# Loop through all records, x is the input, y is the target
# Activation of the output unit
# Notice we multiply the inputs and the weights here
# rather than storing h as a separate variable
output = sigmoid(np.dot(x, weights))
# The error, the target minus the network output
error = error_formula(y, output)
# The error term
error_term = error_term_formula(x, y, output)
# The gradient descent step, the error times the gradient times the inputs
del_w += error_term * x들어온 데이터를 x와 y로 나누어서 순차적으로 처리한다.
위 그림 70번 데이터를 보자면

70번의 x는 0.8, 0.2, 0,0,1,0 이고 y는 0이 된다.
각 x와 weight를 곱셈을하고 sigmoid 처리를 한다. sigmoid된 결과값을 0과 예측값을 error function에 넣어서 error entropy를 구한다. error entropy는 낮은 값일 수록 좋다.
# The error, the target minus the network output
error = error_formula(y, output)본 프로그램에서 이 값은 사용되지 않는다.
# The error term
error_term = error_term_formula(x, y, output)
# The gradient descent step, the error times the gradient times the inputs
del_w += error_term * xBack Propagation을 하는 코드이다.
모든 trainning data를 거치면서 error_term을 업데이트 해서 del_w에 저장한다
저장된 값을 각각의 weight에 업데이트 한다.
# Update the weights here. The learning rate times the
# change in weights, divided by the number of records to average
weights += learnrate * del_w / n_records
정확도 확인
마지막으로 test 데이터와 비교해서 정확도를 확인한다.
test_out = sigmoid(np.dot(features_test, weights))
predictions = test_out > 0.5
accuracy = np.mean(predictions == targets_test)
print("Prediction accuracy: {:.3f}".format(accuracy))
솔직히 이 글을 쓰면서 이해하고 싶었는데, error_term_formula에서 막히고 나니 그 뒤는 이해 할 수 없었다.
시간이 좀 지나면 이해 할 수 있게 될지는 잘 모르겠다.
'AI' 카테고리의 다른 글
| [AI] Ubuntu 22 Nvidia GPU Docker로 연동하기 (0) | 2024.03.31 |
|---|---|
| Sum of the squared errors (0) | 2021.08.01 |
| Backpropagation (0) | 2021.08.01 |
| Feedforward (0) | 2021.07.18 |
| Gradient Descent (0) | 2021.07.18 |
