앞서서 Feedforward를 통해서 weight 값을 update 하는 방법을 알았다.
Feed forward 방식의 update는 Multi-layers가 있는 Neural Network에서는 쉽게 사용이 어렵다.
그래서 나온 방식이 Backpropagation이다.
우선 앞서 나온 내용을 복습해야 한다.
2021.07.17 - [AI] - Gradient Descent
- Sigmoid activation function
$$\sigma(x) = \frac{1}{1+e^{-x}}$$
- Output (prediction) formula
$$\hat{y} = \sigma(w_1 x_1 + w_2 x_2 + b)$$
- Error function
$$Error(y, \hat{y}) = - y \log(\hat{y}) - (1-y) \log(1-\hat{y})$$
- The function that updates the weights
$$ w_i \longrightarrow w_i + \alpha (y - \hat{y}) x_i$$
$$ b \longrightarrow b + \alpha (y - \hat{y})$$
2021.07.18 - [AI] - Feedforward
- Matrix Calculate
$$ \hat{y} = \sigma \begin{pmatrix} {w^{2}}_{11} \\ {w^{2}}_{21} \\ {w^{2}}_{31} \end{pmatrix} \sigma \begin{pmatrix} w_{11} && w_{12} \\ w_{21} && w_{22} \\ w_{31} && w_{32} \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ -2 \end{pmatrix} $$
다음과 같은 다중 Neural Networks가 있다고 생각해 보자.

이것을 Matrix로 표현하면 아래와 같다.
$$ \hat{y} = \sigma \begin{pmatrix} {w^{2}}_{11} \\ {w^{2}}_{21} \\ {w^{2}}_{31} \end{pmatrix} \sigma \begin{pmatrix} w_{11} && w_{12} \\ w_{21} && w_{22} \\ w_{31} && w_{32} \end{pmatrix} \begin{pmatrix} x_1 \\ x_2 \\ 1 \end{pmatrix} $$
여기서 Layer 0의 Matrix는
$$ Layer0 = \begin{pmatrix} w_{11} && w_{12} \\ w_{21} && w_{22} \\ w_{31} && w_{32} \end{pmatrix} $$
이고 Layer 1은
$$ Layer1 = \begin{pmatrix} {w^{2}}_{11} \\ {w^{2}}_{21} \\ {w^{2}}_{31} \end{pmatrix} $$
가 된다.
각 가중치별 Error Function의 Vector 형태로 나타내면 은 $ \frac{\partial{E}}{\partial{W^{0}}_{11}} $ 의 형태로 나타나게 된다. 이것을 표현하면 아래와 같다.
$$ \nabla{E} = \begin{pmatrix} \frac{\partial{E}}{\partial{W^{0}}_{11}} && \frac{\partial{E}}{\partial{W^{0}}_{12}} && \frac{\partial{E}}{\partial{W^{1}}_{11}} \\ \frac{\partial{E}}{\partial{W^{0}}_{21}} && \frac{\partial{E}}{\partial{W^{0}}_{22}} && \frac{\partial{E}}{\partial{W^{1}}_{21}} \\ \frac{\partial{E}}{\partial{W^{0}}_{31}} && \frac{\partial{E}}{\partial{W^{0}}_{32}} && \frac{\partial{E}}{\partial{W^{1}}_{31}} \end{pmatrix} $$
핵심은
- 각 가중치의 변화가 $ \nabla{E} $ 의 위치에 얼마나 영향을 주는가?
가 된다.
이것은 weight의 업데이트에서 사용할 수 있다.
$$ {w'}_i = w_i - \alpha * \partial{E} / \partial{w_i} $$
이 공식을 아래와 같이 표현 가능하다.
$$ w_{ij} \longleftarrow w_{ij} - \alpha (\frac{\partial{E}}{\partial{W^{0}}_{ij}})$$
이제 미분에서 나오는 Chain Rule에 대해서 이해하자.

f(x) = y일때 y = 3x일 경우 y에 대한 x의 미분을 하면 결과는 3이된다. 이 결과를 갖는 y로 z를 미분하면 이것은 2가 되고 이 두개의 미분한 결과 값은 궁극적으로 z를 x로 미분한 값과 같게 된다.
$$ \partial{z}/\partial{x} = \partial{y}/\partial{x} * \partial{z}/\partial{y} $$
로 나타낼 수 있다.
이것을 Neural Network 관점에서 풀어보자면 다음과 같이 말할 수 있다.
- Feed forward는 여러개의 함수를 곱한 결과물이다.
- Back Propagation은 곱한 결과물을 미분하는 것이다.
이제 결과의 미분을 어떻게 Back Propagation하는지 위의 그림에서 z의 결과 값을 6.6로 만약에 변경했다고 생각해 보자. 이것은 기존 결과값에 10%를 더한 목표가 된다.
- 6.6 = 2y = 3.3 = y = 3x = 1.1 = x
x가 1이 들어왔을 때 y가 3.3이 되기위한 weight는 3.3이 됨으로
아래와 같이 weight가 update 될 수 있다.


x의 weight 값을 10% 증가 시킴으로써 목표하는 z의 값을 얻어 낼 수 있다.
반대로 y의 weight값을 10% 올려서 목표하는 z의 값을 역시 얻어 낼 수 있게 된다.
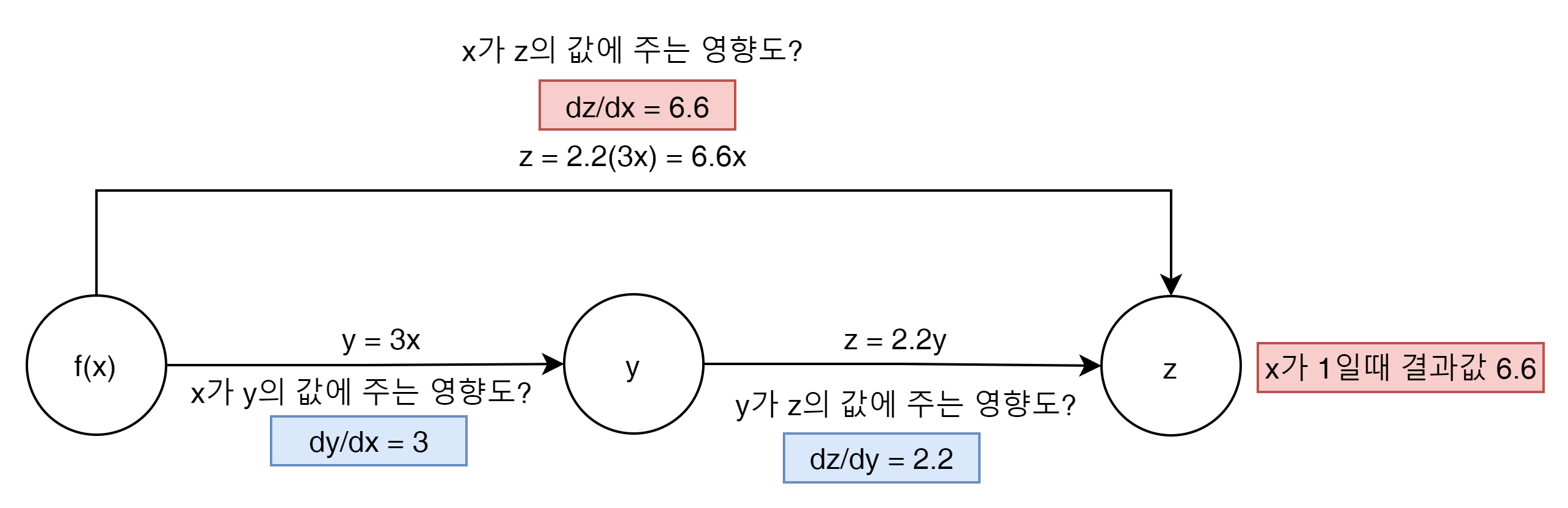
결국 핵심은 x의 값이 z라는 값에 얼마의 변화량을 일으키냐가 핵심이 된다.
그럼 다시 본론으로 돌아가 보자.

이 그림은 다음과 같이 나타낼 수 있다.
$$ \nabla{E} = \begin{pmatrix} \frac{\partial{E}}{\partial{W^{0}}_{11}} && \frac{\partial{E}}{\partial{W^{0}}_{12}} && \frac{\partial{E}}{\partial{W^{1}}_{11}} \\ \frac{\partial{E}}{\partial{W^{0}}_{21}} && \frac{\partial{E}}{\partial{W^{0}}_{22}} && \frac{\partial{E}}{\partial{W^{1}}_{21}} \\ \frac{\partial{E}}{\partial{W^{0}}_{31}} && \frac{\partial{E}}{\partial{W^{0}}_{32}} && \frac{\partial{E}}{\partial{W^{1}}_{31}} \end{pmatrix} $$
이 것을 바탕으로 Layer 0 (영어로 Superscript라고 부른다)의 $ W_{11} $ 이 $ \nabla{E} $ 에 어떤 영향을 주는지 Chain rule을 사용해 보자.
$$ \frac{\partial{E}}{\partial{{W^0}_{11}}} = \frac{\partial{E}}{\partial{\hat{y}}} * \frac{\partial{\hat{y}}}{\partial{h}} * \frac{\partial{h}}{\partial{h1}} * \frac{\partial{h1}}{\partial{{W^0}_{11}}} $$
이중에 h1 변화에 따른 h의 변화율은 다음과 같이 표현 할 수 있다.
$$ h = W^{1}_{11} + W^{1}_{12} $$
일때 h1으로 미분하면
$$ \partial{h} / \partial{h_1} = W^{1}_{11} * \sigma{(h1)} * (1 - \sigma{(h1)}) $$
이 된다.
Sigmoid의 미분은 다음 내용을 참고하자.
https://towardsdatascience.com/derivative-of-the-sigmoid-function-536880cf918e
2021.07.17 - [AI] - Sigmoid Function
이에 대한 관련 코드는 다음 github를 참고 하자.
'AI' 카테고리의 다른 글
| Sum of the squared errors (0) | 2021.08.01 |
|---|---|
| Predicting Student Admissions with Neural Networks (0) | 2021.08.01 |
| Feedforward (0) | 2021.07.18 |
| Gradient Descent (0) | 2021.07.18 |
| Error Function (0) | 2021.07.18 |
